基于改进Hilbert分析的陀螺电机轴承保持架故障特征识别
2018-07-25朱玉鹏晋会杰谢鹏飞牛青波杨茹萍
朱玉鹏, 晋会杰,谢鹏飞, 牛青波,杨茹萍
(1.河南科技大学 土木工程学院,河南 洛阳 471003;2.商丘工学院,河南 商丘 476000;3.洛阳轴承研究所有限公司,河南 洛阳 471039)
在航空航天、汽车、工程机械领域,轴承常处于变速、变载等典型工况条件或极端环境,运行过程中滚动体与保持架的碰撞不可避免[1-5],系统表现出复杂的非线性动力学特性[6-7],保持架成为轴承故障高发部位。目前,针对保持架的研究大多集中在保持架数值仿真模型的动力学特性研究领域[8-9],关于保持架状态识别及故障诊断研究的相关工作很少。
陀螺电机轴承主要元件由高强度合金钢制成,保持架则采用非金属材料,其刚度和质量均远小于内、外圈,导致轴承系统中保持架故障特征频率振动量级小,常常堙没在复杂噪声背景下,传统信号分析方法很难识别。且保持架一旦发生故障,振动传递路径复杂,测试采集到的信号大多是多分量调幅调频信号,如何在强噪声、复杂调制背景下识别保持架频率是保持架故障诊断的关键。
HHT(Hilbert-Huang Transform)具有良好的时频特性,且其自适应的分解模式非常适合非线性和非平稳信号的分析[10-11],具有很高的信噪比,在处理调制信号方面效果良好[12-14]。因此,采用基于自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition With Adaptive Noise,CEEMDAN)算法对HHT进行改进,并与自动提取敏感IMF分量算法相结合,通过对实测保持架故障轴承振动信号的特征提取,验证该方法的有效性。
1 改进的HHT方法
1.1 CEEMDAN
CEEMDAN是在经验模态分解(EMD)[15-16]的每个阶段有限次添加自适应白噪声,通过计算唯一余量信号获取固有模态函数(IMF),在消除模态混叠[17-18]的同时降低了噪声残留。
假设Ek(·)为EMD处理后得到的第k个IMF,且令w(i)为一个零均值单位方差的白噪声,则CEEMDAN算法的具体步骤为:
1)采用EMD算法对x(i)=x+β0w(i)进行分解,得到第1个CEEMDAN的IMF,即
2)计算第1个残差:r1=x-f1。
3)采用EMD计算r1+β1E1(w(i))的第1个模态,并定义为CEEMDAN的第2个IMF,即
4)当k=1,…,K,计算第k个残差rk=xk-1-fk。
5)采用EMD计算rk+βkEk(w(i))的第1个模态,并定义为CEEMDAN的第k+1个IMF,即
6) 当k=k+1时,返回至第4步,计算CEEMDAN的下一个IMF。
为验证CEEMDAN算法的有效性,对仿真信号进行CEEMDAN处理,添加白噪声50次,幅值为仿真信号标准差的0.01倍,最大筛选迭代次数为100次。分解结果如图1所示,从图中可以看出,脉冲信号和正弦信号清晰地分解到了不同的IMF中。

图1 CEEMDAN分解IMF图Fig.1 Diagram of IMFs by CEEMDAN
1.2 敏感IMF选择算法
对信号进行CEEMDAN处理后故障特征成分会分解到某一个或几个敏感IMF中,信号特征提取的关键在于敏感IMF的选取。因此,提出一种基于相关系数与峭度指标结合的敏感IMF选择算法。
以各IMF与原始信号的相关系数作为统计指标,相关系数越大,则IMF与原始信号相关程度越高,即为目标敏感IMF。为使结果清晰且减小幅值较小的真实IMF分量被剔除的可能性,将所有IMF与原始信号进行归一化处理,各IMF与原始信号的归一化相关系数ci(i=1,2,…,K)为
阈值Q定义为归一化相关系数ci的标准差。若ci>Q,则保留相对应的IMF;若ci≤Q,则相应的IMF不作分析。
峭度为量纲一的参数,与结构尺寸、载荷分布无关,但受脉冲信号影响较大,轴承表面出现损伤类故障时峭度指标变化明显[19]。轴承无故障运转时,时域信号波形平稳无明显尖锐波峰,峭度指标值接近3;一旦轴承存在局部故障,由周期旋转引起的故障部位脉冲信号持续出现,信号波形尖峰程度加剧,峭度值会随之增大,当峭度指标值大于3时,表明轴承已出现故障,大于8时故障已十分明显。设定峭度阈值为3,进行敏感IMF筛选。
综上,采用归一化相关系数和峭度值相结合的算法来进行敏感IMF提取,可以凸显潜在的故障成分,削弱噪声信号影响,从而实现故障特征全面、有效地提取。
1.3 改进的HHT方法
基于以上分析,改进的HHT分析方法的主要步骤为:1)采用CEEMDAN算法对采集的保持架故障信号进行本征模态分解,得到一组IMF;2)分别计算各阶IMF与原始信号的归一化相关系数并计算其标准差,计算各阶IMF峭度指标,根据归一化相关系数和峭度指标综合筛选敏感IMF;3)对筛选得到的IMF进行Hilbert变换包络并进行频谱分析;4)根据包络谱对振动信号进行特征提取和故障诊断。
2 陀螺电机轴承保持架故障实例分析
研究对象为某挠性支承陀螺仪中存在保持架故障的轴承,其具有结构精密、体积小、转速高等特点,且不可拆卸,测试过程中振动传递路径复杂,信号噪声较大。其中的结构固有振动与轴承工作状况无关,仅取决于系统的质量、材质、形状等,属于噪声信号;由Hertz弹性接触理论产生的振动信号为特征信号,其大小取决于轴承结构尺寸以及工作转速,能反映轴承的损伤部位,是进行轴承故障诊断的重要依据。
该陀螺电机轴承为角接触球轴承,具体参数见表1,保持架材料为多孔聚酰亚胺。由于结构复杂,采用在特制底座上粘贴PCB加速度传感器的方法进行振动信号采集,采集工作由LMS Signature Testing系统完成。分析工作则由MATLAB软件完成。测试转速为18 000 r/min,采样频率25 600 Hz,频率分辨率0.781 25 Hz,采样时间0.64 s,计算可得保持架故障特征频率fc为112.1 Hz。

表1 轴承结构参数Tab.1 Structural parameters of bearing
故障轴承时域即FFT频谱图如图2所示。时域信号波动较大、冲击振动明显。频谱图中,低频段仅能发现300 Hz的成分,其为转子转动频率;在1 000~8 000 Hz内频率分布密集,其中3 374 Hz接近保持架故障特征频率30倍频,但峰值相对较低,整体难以发现保持架低频故障成分,无法得出准确结论。

图2 轴承时域信号及频谱图Fig.2 Time domain signal and frequency spectrum of bearing
为实现保持架故障特征的准确提取,利用改进的HHT算法对图中时域信号进行分析处理。CEEMDAN算法参数设置:白噪声幅值为振动信号标准差的0.1倍,白噪声添加598次,最大迭代次数500。CEEMDAN处理后共得到19个IMF,包含主要信息的前5阶IMF如图3所示。各IMF与原始信号的归一化相关系数以及峭度指标如图4所示。
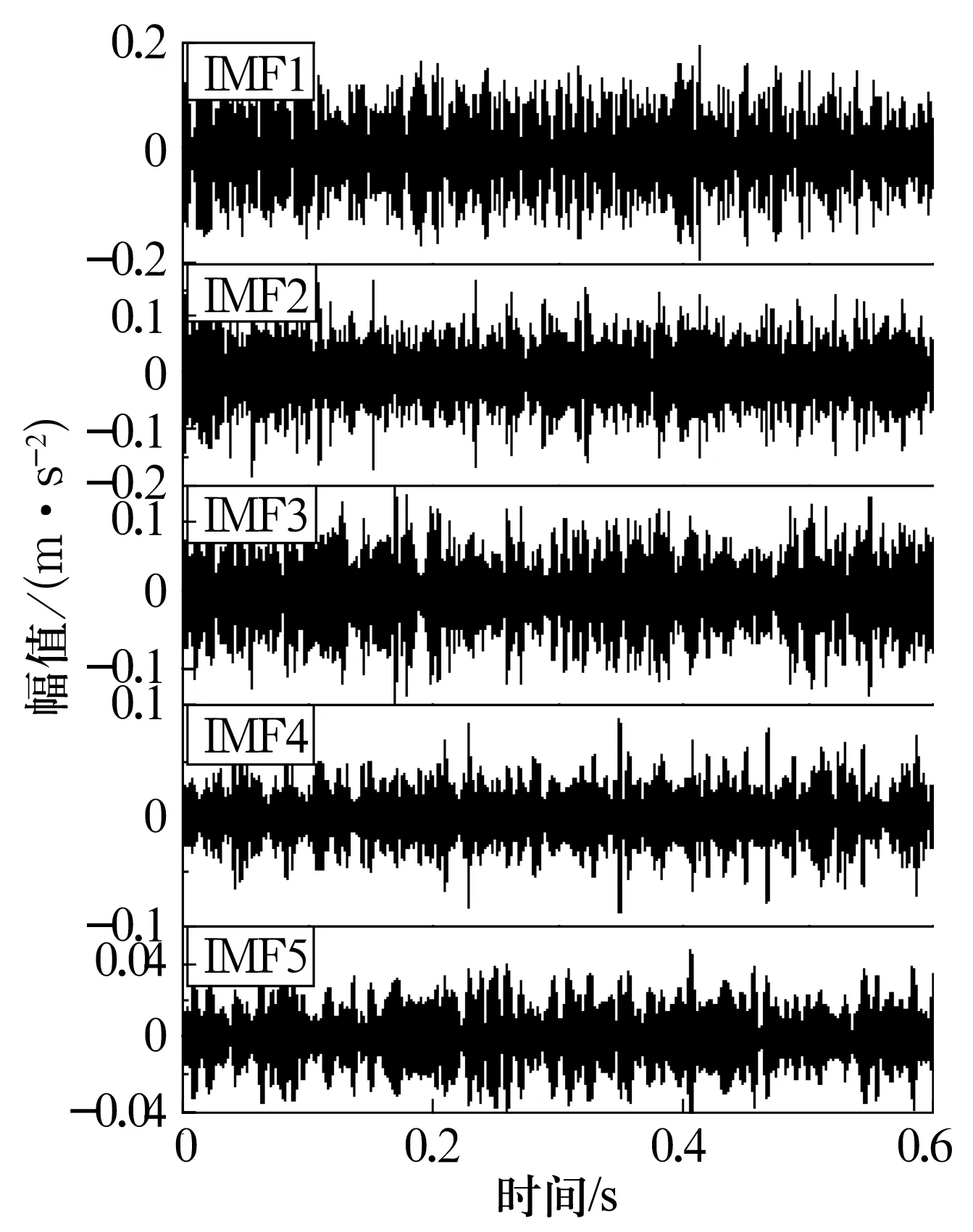
图3 CEEMDAN处理后部分IMF图Fig.3 Diagram part of IMFs after CEEMDAN
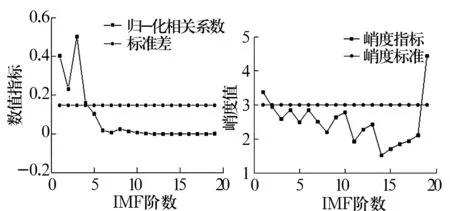
图4 各IMF相关系数及峭度指标Fig.4 Correlation coefficient and kurtosis index of all IMFs
根据自相关系数法,筛选得到敏感分量为IMF1,IMF2,IMF3和IMF4;根据峭度指标则得到敏感分量为IMF1和IMF19。由于IMF19已接近残差分量且几乎不包含频率信息,故最终选择IMF1为敏感分量。
对IMF1进行Hilbert包络分析,结果如图5所示。从图中可以看出,Hilbert包络谱中最大峰值出现在112.5 Hz处,与保持架故障特征频率相对应,另外还可发现保持架故障特征频率的不同倍频,由此可以得出保持架处于动不平衡状态[20],与实际情况相一致。
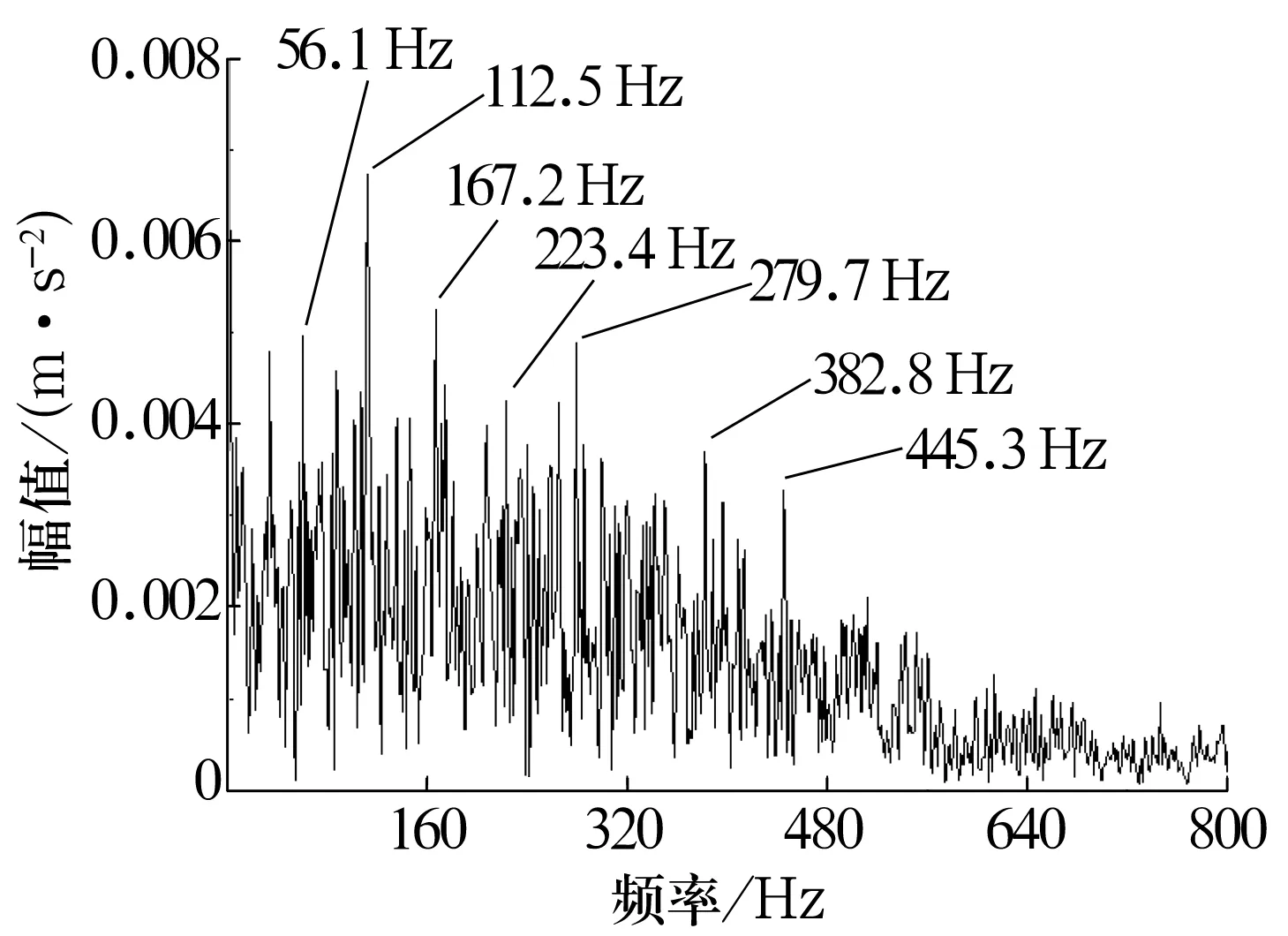
图5 IMF1的包络谱Fig.5 Envelope spectrum of IMF1
3 结论
1)CEEMDAN算法有效降低了模态混叠,结合自相关系数、峭度指标筛选法则,可准确筛选出敏感IMF,剔除了无故障IMF的干扰。Hilbert包络谱分析能从高频采样的频谱中识别出振动能量较小的低频部分,使之不会湮没在复杂噪声背景中,适合强噪声条件下振动信号分析。
2) 由于结构原因,轴承保持架转速低于转子;且刚度远小于内圈、外圈、球等元件,故障振动频率小、量级低。如果振动测试信号中出现保持架故障特征频率,则反映保持架出现缺陷,处于动不平衡状态,属于轴承保持架动不平衡故障现象。
