摩擦因数对单排球转盘轴承接触次表层的影响

王委，陈捷，洪荣晶，何培瑜

(南京工业大学 机械与动力工程学院，南京 210009)

转盘轴承是传递载荷、完成相对回转运动的关键零部件，广泛应用于挖掘机械、起重机械、采矿机械、港口机械、以及军事、科研设备等领域[1]。国内外学者对转盘轴承的力学性能和疲劳损伤进行了研究。文献[2-3]研究了四点接触转盘轴承在轴向载荷、径向载荷和倾覆力矩作用下球的强度对转盘轴承承载的影响。文献[4]通过模拟球与沟道接触的二维接触模型，指出次表层的最大应力是使沟道产生剥落的一个重要原因。文献[5]利用ABAQUS得到了转盘轴承在倾覆力矩作用下的载荷分布情况，与理论计算结果误差较大，指出了由于接触角的变化，有限元结果更加合理。文献[6]建立和求解了转盘轴承的弹性有限元接触模型和弹塑性有限元接触模型，得到了各个零件的应力应变云图，并结合实际工况分析了沟道失效的原因，但并未考虑接触次表层正交剪应力的影响。文献[7]利用有限元软件建立了球与沟道弹性接触模型，分析了大型滚动轴承球与沟道接触应力、沟道次表面应力场及应变场随深度的变化规律。文献[8]建立了球与沟道接触的模型，对比了球在静止和滚动状态下的正交剪应力的变化，发现相比静止状态，滚动时最大正交剪应力的深度减小，位置向沟道表面移动，正交剪应力变化幅值有所增大，但没有比较不同摩擦因数下接触次表层的正交剪应力的变化情况。文献[9-10]的研究表明，接触疲劳次表层裂纹的萌生位置与最大正交剪应力位置一致。目前，多数学者认为沟道的疲劳损伤源自于沟道次表层的最大正交剪应力。

鉴于此，通过ABAQUS仿真模拟与Hertz理论计算，研究不同摩擦因数对转盘轴承接触次表层正交剪应力和等效应力的影响，并对次表层接触疲劳损伤进行分析。

1 理论计算

用Hertz理论求解转盘轴承承载时的接触应力和变形[11-12]，其接触示意图如图1所示。假设平面1内接触体a和b的半径分别为ra1和rb1；平面2内接触体a和b的半径分别为ra2和rb2，接触区域表面为椭圆形(图2)[8]17。

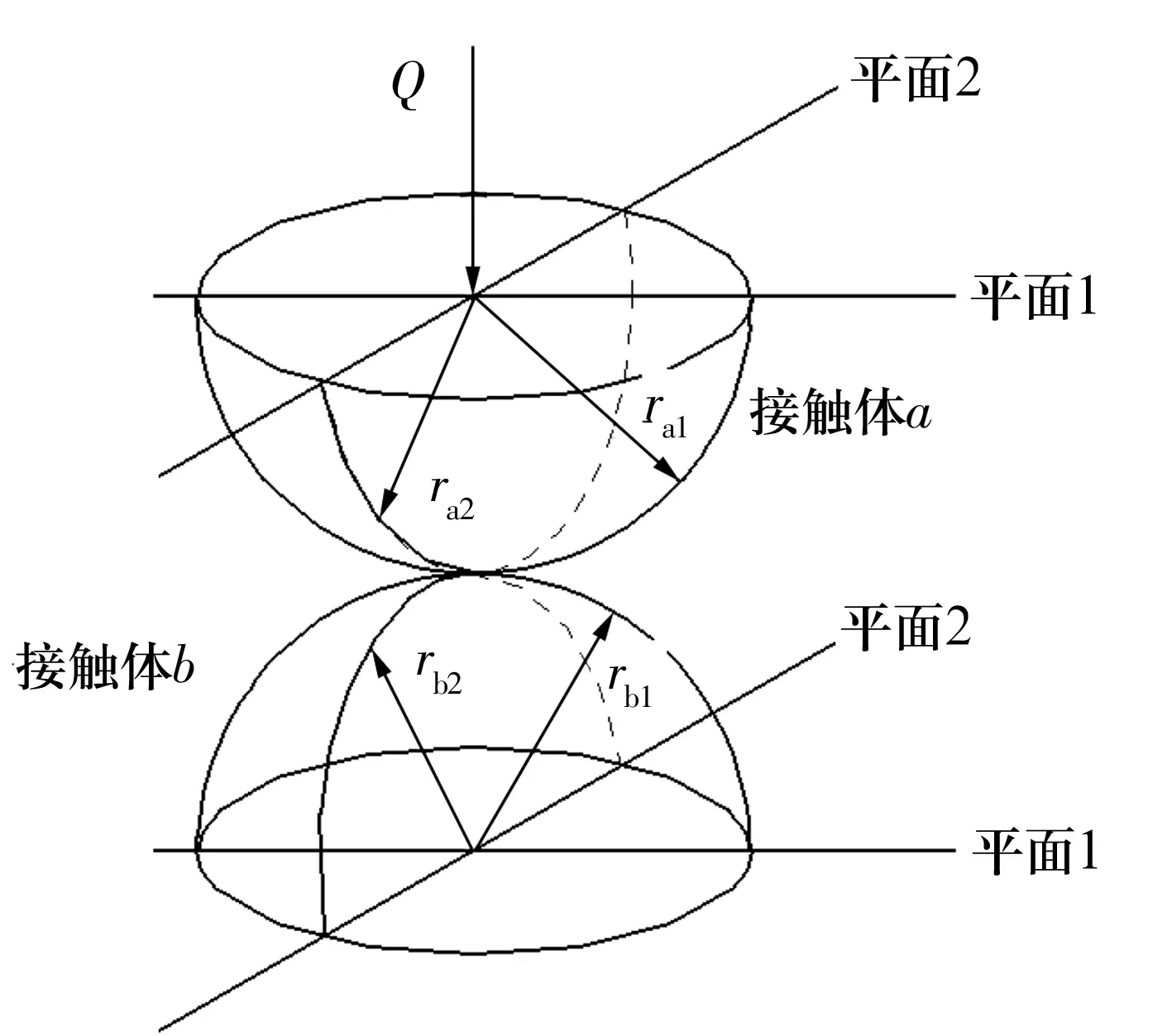
图1 Hertz接触示意图Fig.1 Diagram of Hertz contact

图2 转盘轴承局部接触截面图Fig.2 Sectional diagram of local contact of slewing bearing

Hertz最大接触应力Pmax为[6]12-16

(1)

∑ρ=ρ11+ρ12+ρ21+ρ22，

(2)

式中：a，b分别为接触椭圆的长、短半轴；ν1，ν2分别为球和沟道的泊松比；E1，E2分别为球和沟道的弹性模量；Q为法向载荷；Z为球数；Fa为轴向力；α0为初始接触角；∑ρ为曲率和；ρ11，ρ12，ρ21，ρ22分别为主平面1球、主平面2球、主平面1沟道、主平面2沟道的曲率；R为接触面法线方向上内圈沟道半径；Dw为球径；D1为外圈沟道直径；t为曲率比；Ri为外圈沟道上圆周截面半径；F(ρ)为曲率差(即cosτ)；α，β为与曲率差有关的量纲一的量，可以根据F(ρ)通过查表[13]得出。

取JB/T 2300—2011《回转支承》中的转盘轴承(型号为010.20.200.00)为研究对象，Z=24，Dw=20 mm，Dpw=200 mm，α0=45°，t=1.08，Fa=300 kN。将以上参数值代入上式可以得出球与外圈的接触椭圆中a=3.48 mm，b=0.62 mm，Pemax=3 912 MPa，球与内圈的最大接触应力Pimax=3 956 MPa。Hertz研究表明，最大正交剪应力出现在接触区域次表层，距离接触表面深度大约为0.5b，应力约为0.25Pmax，其方向关于接触中心对称[14]。

2 有限元仿真

2.1 模型建立

为了提高有限元软件的计算效率，取转盘轴承的1/24，对球与沟道接触区域进行网格划分。转盘轴承套圈材料为50Mn，球材料为GCr15,且在弹性变形范围内采用各向同性线弹性材料模型。材料的主要力学特性见表1。

表1 转盘轴承的材料特性Tab.1 Material properties of slewing bearing

2.2 网格划分

采用六面体网格，单元类型为C3D8I。设置3个分析步，在初始分析步后增加一个分析步使接触关系平稳建立，在转盘轴承运转过程中，球与内外圈沟道分别存在接触关系，接触类型选择为普通的“面与面”接触，球为主面，沟道为从面。同时，设置球与沟道之间的切向作用为罚接触，摩擦因数μ分别取0.1，0.2，0.3，0.4，0.5，法向接触为默认值“硬接触”。

图3 网格划分Fig.3 Meshing

2.3 边界条件

将转盘轴承内圈固定，验证的静止模型在内外圈端面上施加循环对称边界条件，而旋转模型在转盘轴承外圈施加速度和载荷，在外圈中心建立参考点,与外圈外表面建立耦合约束关系。在外圈上表面施加轴向力，外圈端面释放y方向旋转自由度和x，y，z方向平移自由度；球不设约束，由摩擦力带动旋转，外圈设置旋转速度0.065 4 rad/s。

3 结果与分析

球与套圈的接触应力分布如图4所示。由图可知，球与内、外圈的最大接触应力分别为4 006，3 996 MPa，其值和位置都与Hertz理论计算结果非常接近，证明了有限元模型的正确性。

图4 球与套圈接触应力分布图Fig.4 Diagram of contact stress distribution between ball and ring

当外圈静止时，轴向截面的球与套圈接触的等效应力如图5所示。由图可知，最大等效应力为2 529 MPa，出现在与内圈滚道接触的球的次表层上，而且接触次表层的等效应力比沟道表面的大很多。当外圈静止时，球与内圈接触的正交剪应力分布如图6所示，由图可知，内圈的正交剪应力相对于接触中心基本成对称分布，有限元计算的最大剪应力值为891.2 MPa，略小于0.25Pimax，深度为0.3 mm，约为0.5b。

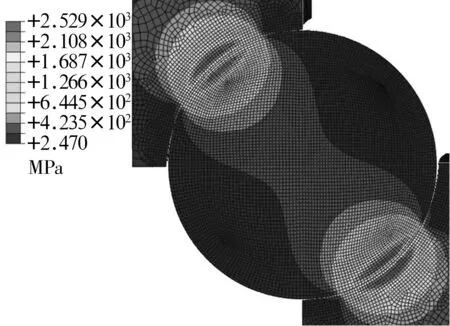
图5 轴向截面的等效应力分布图Fig.5 Diagram of equivalent stress distribution of axial section

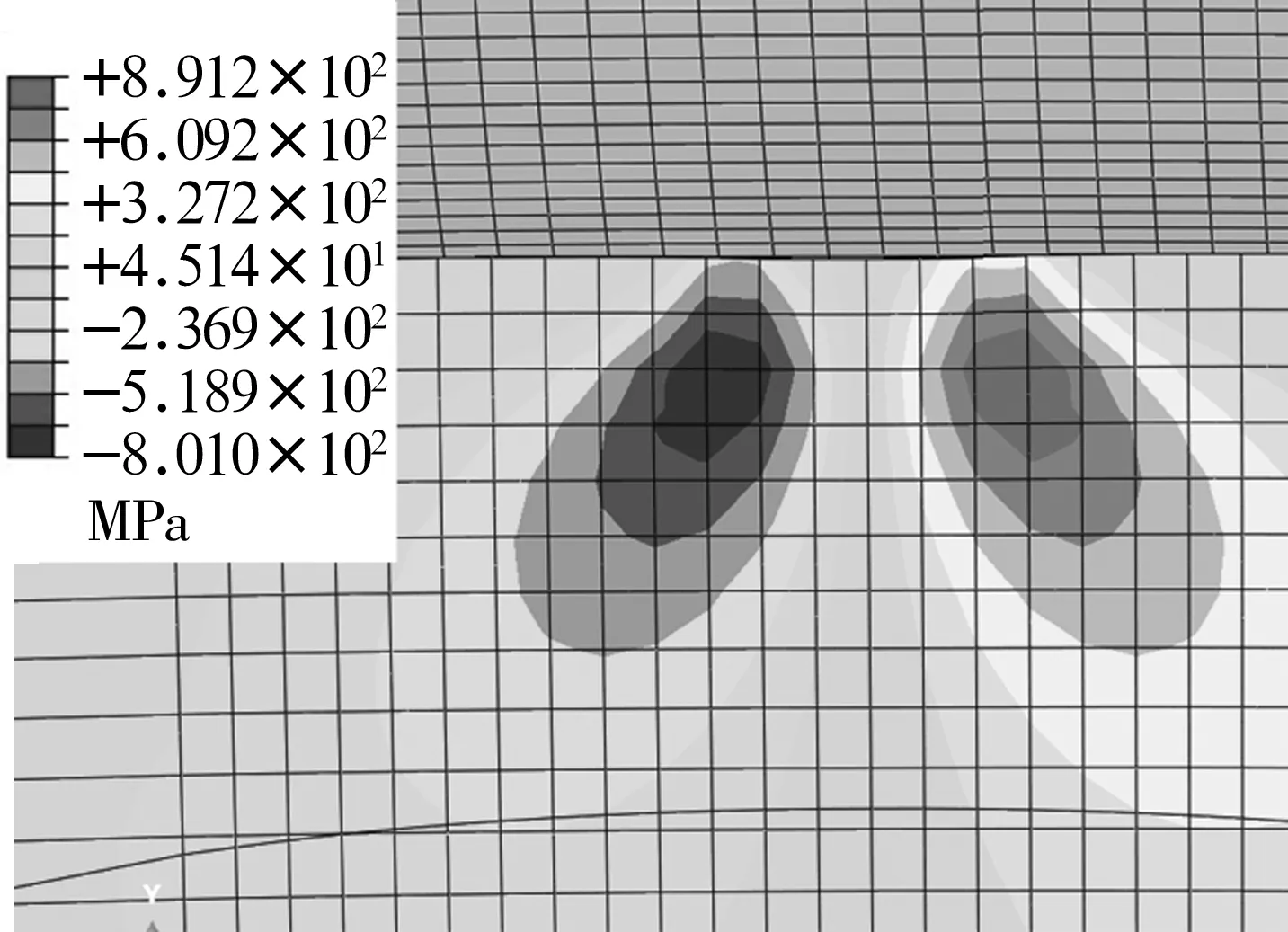
图6 球与内圈接触的正交剪应力分布Fig.6 Orthogonal shear stress distribution of contact between ball and inner ring

滚动轴承在工作中，当载荷与内圈相对静止时，内圈先发生疲劳破坏，此时计算轴承寿命时利用内圈上的最大交变应力及应变计算内圈沟道的疲劳寿命[7]37。分析不同摩擦因数下内圈沟道的正交剪应力和等效应力，结果分别如图7、图8所示。

由图7可知，摩擦力使沟道截面上的最大正交剪应力关于接触中心不对称，随着摩擦因数的增大，最大正交剪应力有所增加,且最大正交剪应力位置向沟道表面移动。实际的转盘轴承运转中，由于润滑不良导致疲劳损伤萌生位置深度变浅。由图8可知，等效应力随着摩擦因数的增大有所增加，且最大值有向沟道表面移动的趋势。

图7 不同摩擦因数下内圈沟道的正交剪应力Fig.7 Orthogonal stress of inner ring raceway under different friction coefficients

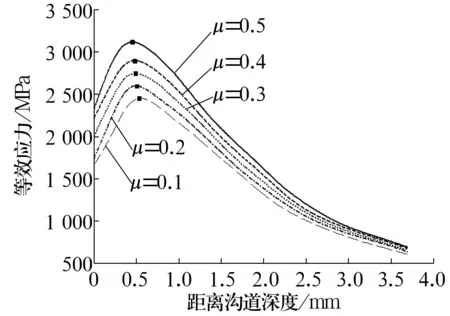
图8 不同摩擦因数下内圈沟道的等效应力Fig.8 Equivalent stress of inner ring raceway under different friction coefficients

4 摩擦因数对疲劳寿命的影响

转盘轴承疲劳分析可利用σ-N法，其计算过程为：1)用理论方法或有限元法计算零件疲劳部位的各向应力，包括最大值、最小值、平均应力及应力幅值；2)通过Von-Mises畸变能理论计算等效应力、等效应力幅值、等效平均应力，沟道受压时，等效平均应力为等效应力幅值的相反数；3)通过分析模型计算反向弯曲应力；4)根据寿命计算公式计算疲劳寿命。根据Basquin公式计算疲劳寿命为[7]38

(3)

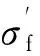
(4)

σaeq=

σmeq=

式中：Rm为抗拉强度，Rm=1 134 MPa[15]；σaeq为等效应力幅值；σmeq为平均等效应力；σa1，σa2，σa3为沟道次表面3个主方向的应力，且σa1>σa2>σa3；σm1,σm2,σm3为3个方向的平均应力，且σm1>σm2>σm3。提取不同摩擦因数下有限元模型的3个主方向应力，根据上式先计算等效应力幅值和平均等效应力，再计算寿命(应力循环次数)，其随摩擦因数的变化曲线如图9所示。由图可知，随着摩擦因数的增大，寿命呈递减的趋势。

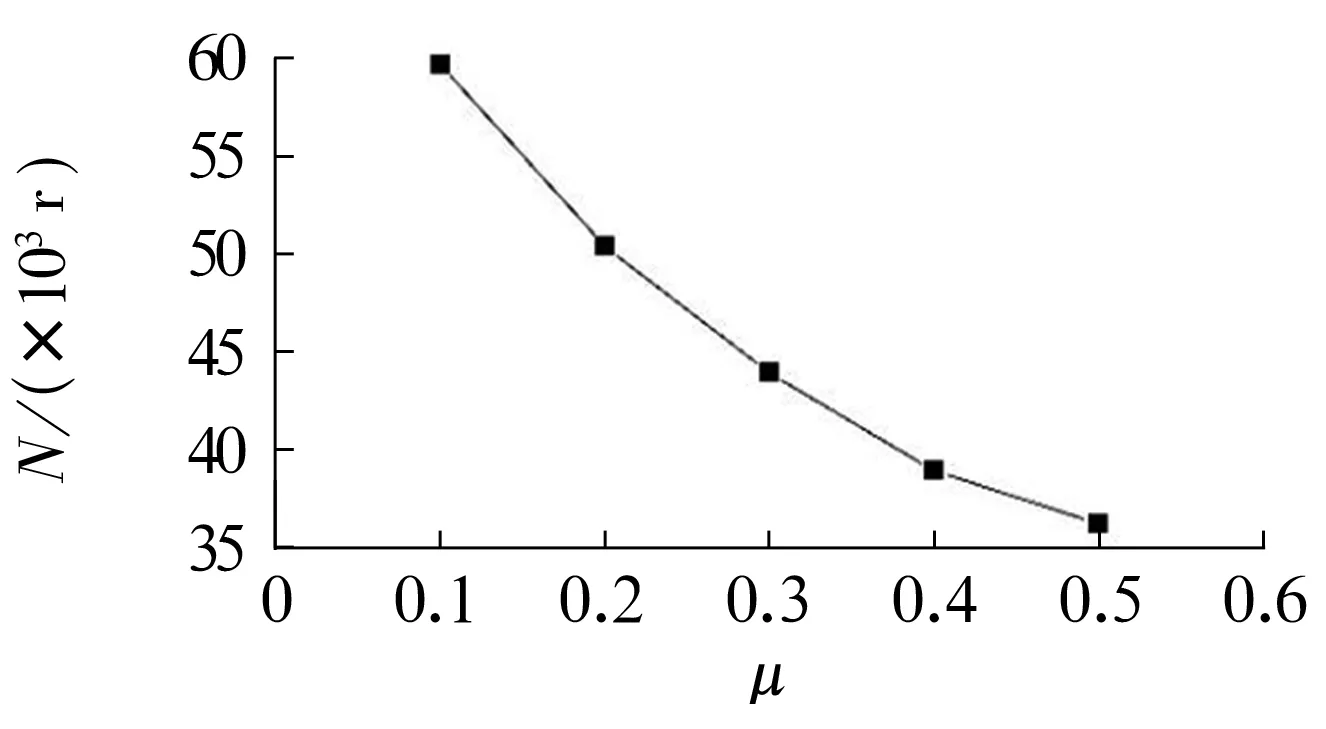
图9 寿命随摩擦因数的变化曲线Fig.9 Variation curve of life with friction coefficients

5 结束语

通过ABAQUS建立转盘轴承有限元模型，对球与套圈接触次表层的正交剪应力和等效应力进行分析，研究了摩擦因数对轴承接触应力和疲劳寿命的影响，结果表明：转盘轴承球与套圈的接触几何和应力分布与Hertz理论基本一致，最大等效应力和正交剪应力出现在接触区域的次表层。摩擦力使次表层的正交剪应力关于接触中心不对称。随着摩擦因数的增大，最大正交剪应力值和等效应力均呈增大的趋势，且向接触表面移动，寿命减小。