基于前置、后置策略的快速排序算法研究
2018-07-25张晓煜
张 晓 煜
(西藏民族大学 信息工程学院,陕西 咸阳 712082)
0 引言
排序是计算机科学中重要的研究问题,2000年被列为对科学和工程计算研究与实践影响最大的十大问题之一[1]。排序操作在计算机图形学[2]、生产调度[3]、模式识别及电力系统[4-5]等领域都有广泛的应用。而快速排序就其平均性能而言是各种排序算法中性能最好的一种排序方法。[6]假设区间[s,t]上的原始待排序列为{L.r[s],L.r[s+1],…,L.r[t]},快速排序(Quick Sort)的基本思想是:首先任意选取一个记录(通常可选第一个记录L.r[s])作为枢轴(或支点,pivot),然后按下述原则重新排列其余记录:将所有关键字较枢轴记录关键字小的记录都安置在枢轴记录所在位置之前,将所有关键字较枢轴记录关键字大的记录都安置在枢轴记录所在位置之后。由此可以将该“枢轴”记录最后所落的位置i作分界线,将序列{L.r[s],…,L.r[t]}分割成两个子序列{L.r[s],L.r[s+1],…,L.r[i-1]}和{L.r[i+1],L.r[i+2],…,L.r[t]}。这个过程称作一趟快速排序(或一次划分)。
1 基于前置、后置方法实现快速排序一趟划分的具体分析
基于前置、后置策略的快速排序算法由于避免了枢轴记录在最终位置确定之前与待排记录之间无谓的交换,因而成为目前普遍采用的快速排序算法。具体的算法描述如下(算法1)[2]:
int Partition(Sq_List &L, int low, int high )
{
L.r[0]=L.r[low]; //选取子表中第一个记录作为枢轴记录
privotkey=L.r[low].key; //枢轴记录关键字
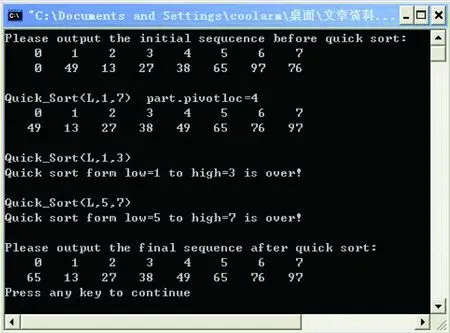
while(low {while(low L.r[low]=L.r[high]; //将比枢轴记录小的记录移到低端 while(low L.r[high]=L.r[low]; //将比枢轴记录大的记录移到高端 } L.r[low]=L.r[0]; //枢轴记录到位 return low; //返回枢轴记录位置 } (1)上述Partition算法取原始待排序列中第一个记录作为枢轴记录,先将枢轴记录赋值给0号监视哨,然后从后往前扫描将较枢轴记录大的记录关键字前置(即将其记录关键字赋值给枢轴记录原先所占位置的记录关键字),容易看出,如果前置操作发生,那么低位指针当前所指位置的记录关键字必定小于枢轴记录关键字。接下来由前往后扫描,将较枢轴记录大的记录关键字后置过程中没有必要再进行此次比较。同理,如后置操作发生,那么高位指针当前所指位置的记录关键字必定大于枢轴记录关键字。再接下来由后往前扫描中没有必要再进行此次比较。这两次无谓的比较应该予以避免。 (2)上述Partition算法中高位指针由高向低及低位指针由低向高两者交替单向移动的过程中,只是根据当前指针所指记录关键字和枢轴记录关键字之间的大小关系决定是否执行前置、后置操作。对于指针移动过程中两相邻记录之间关键字是否逆位序并未考虑。此外前置操作之后指针i所指记录与其直接前驱之间以及后置操作执行之后指针j所指记录与其直接后续之间是否存在逆位序也未考虑。 综上,本文在文献[6]的基础上,在前置、后置操作执行后亦在相邻记录关键字之间进行逆位序的调整,则可得到改进后的算法(算法2): typedef struct { int pivotloc; //关键字项 int swap; bool over; }Part_loction; //记录类型 Part_loction partition(Sequence_List &L, int i, int j) { Part_loction part; //定义结构体变量part part.swap=0;part.over=0;int privotkey,low=i,high=j; L.r[0]=L.r[low]; //使用子表中第一个记录作为枢轴记录 privotkey=L.r[low].key; //枢轴记录关键字 while(i {while(i {if(L.r[j].key>L.r[j+1].key && j!=high) //高位指针j后退过程中加入起泡思想 { L.r[j] <—>L.r[j+1]; part.swap++;} j--; //指针j后退1个位置,进行下一次比较 }// while1 if(i==j) //while1执行后,有可能导致i==j,即枢轴记录最终位置已确定 break; //当i==j成立时,应及时退出外层while循环 L.r[i]=L.r[j]; //当前指针j所指记录关键字小于枢轴记录关键字,执行前置操作 if(L.r[i-1] >L.r[i] && i>low) //前置操作执行后判断相邻记录关键字是否逆位序 { L.r[i-1] <—> L.r[i] } i++; //前置操作执行后且判断相邻记录关键字是否逆位序,已判断指针i自加 while(i {if(L.r[i-1].key>L.r[i].key && i!=low) //同理低位指针i前移过程中加入起泡思想 { L.r[i-1].key<—> L.r[i].key; } i++;}//while2 //前置操作执行后指针i自加避免下一轮从前往后扫描时一次无谓的比较 if(i==j) //最近的while2执行后,亦有可能导致i==j,即枢轴记录最终位置已确定 break; //当i==j成立时,应及时退出外层while循环 L.r[j]=L.r[i]; //若i!==j顺序执行后置操作 if(L.r[j].key>L.r[j+1].key && j {L.r[j]<—>L.r[j+1].key; } j--; //同理,后置操作执行后且相邻记录关键字是否逆位序已判断指针j自加 } //外层大while if(i==low && part.swap==0) part.over=1; //若i指针始终在低位,且j指针在移动的过程中没有发现逆位序 else { L.r[i]=L.r[0]; //枢轴记录到位 part.pivotloc=i; //返回划分位置序号 } return part; //返回结构体变量part }//partition 改写后的Partition划分算法中,在指针j由高位后退的过程中加入起泡思想,判断相邻记录关键字之间是否存在逆位序,若存在则交换相邻记录消除逆位序。此外,当前置操作执行后, 判断i所指记录关键字与i-1所指记录关键字之间是否存在逆位序, 若存在则交换消除逆位序。同时低位指针i前移的过程中亦做了类似处理消除相邻记录之间可能存在的逆位序。同理,当后置操作执行后判断j指针所指记录关键字与j+1所指记录关键字之间是否存在逆位序,若存在则交换相邻记录消除逆位序。 此外,改写后的算法2中返回值采用结构体类型变量part。其中:结构体成员变量part.swap[4]用来标志是否存在逆位序,part.over[4]用来标志待排序列是否已经非递减有序。需要说明的是,由于枢轴记录选用的是L.r[low],若指针j后退的过程中没有发生逆位序交换,且指针j 最后回退至j==i==low,即枢轴记录最后落的位置就是它的初始位置。根据快速排序的算法思想所有较枢轴记录关键字大的记录均落在枢轴记录后面且彼此之间不存在逆位序,则可断言区间[low,high]上待排元素已非递减有序。 以初始待排序列{49,13,27,38,65,97,76}为例,采用算法1中的划分函数运行结果如图1所示,而采用算法2中的划分函数运行结果如图2所示。 图1 原Partition算法运行结果 图2 改进后的Partition算法运行结果 从运行结果可以看出,针对运行示例{49, 13, 27, 38, 65, 97, 76},原算法需调用10次划分,而改进后的算法则只需调用3次划分即可完成排序。 文献[6]中所示算法1在待排列已经排好序的情况下,其递归树成为单支树,每次划分只得到1个比上次少1个记录的子序列,时间复杂度为O(n2)。 表1 待排序列非递减有序时算法2时间复杂度分析 对于表1所示的非递减待排序列以第一行枢轴记录选取29为例,在算法2的执行过程中,当指针j指向7号位置时,7号记录关键字9和枢轴记录关键字29进行了一次比较;当i指针为2、3、4、5、6时,i指针分别与其直接前驱进行了5次比较,因此,共计进行了6次比较。此外,i指针由前向后移动时分别遇到{21,18}、{21,16}、{21,14}、{21,12}这4个逆位序,消除1个逆位序需要3次赋值操作。再加上枢轴记录关键字29放到0号监视哨进行了1次赋值操作,当指针j指向7号位置时经比较进行了1次赋值操作(将7号记录关键字9赋值到1号位置),最后将枢轴记录关键字29写入其最终所落的7号位置时进行了1次赋值操作。因此,共计进行了3次赋值操作。别的情况类似,不再赘述。分析表1所展示的最坏情况下原始待排序列的赋值次数和比较次数,推广至含n个元素的非递减待排序列时,容易得出最坏情况下算法2的时间复杂度仍为O(n2),同算法1的时间复杂度。 #include"iostream.h" #include"stdlib.h" #include "time.h" typedef int KeyType; //定义关键字类型为整数类型 typedef struct { KeyType key; //关键字项 }RecordType; //记录类型 typedef struct { RecordType r[20000+1]; //r[0]用作监视哨 int length; //顺序表长度 }Sequence_List; //顺序表类型 typedef struct { int pivotloc; //关键字项 int swap; bool over; }Part_loction; //记录类型 voidsrand (unsigned int seed); voidInitial_sequence(Sequence_List &L) { //函数功能依条件产生L.length个随机数 L.r[0].key=0; srand(time(0)); //srand函数用来初始化随机数发生器, time(0)返回的是系统的时间(从1970-01-01午夜算起) //单位:秒,此处用time(0)的返回值做为初始化种子 for(int i=1;i<=L.length;i++) L.r[i].key=rand( )%150; //随机产生150以内的整数 }//Initial_sequence voidprint_Sequence_List_L(Sequence_List &L, int low, int high) { //从当前调用的低子表端到高子表端依次输出待排元素 int i; for(i=low; i<=high; i++) { if(L.r[i].key<=9) //若为个位数,前面输出4个空格 cout<<" "< else if(L.r[i].key<=99) //若为2位数,前面输出3个空格 cout<<" "< else cout<<" "< if(i%10==0) //每输出10个数回车换行1次 cout< }//for }//print_Sequence_List_L Part_loction partition(Sequence_List &L, int i, int j) { //在待排区间 [i...j]进行划分枢轴记录到位,并返回其所在的位置 Part_loction part; //定义结构体变量part part.swap=0; part.over=0; int privotkey, low=i, high=j; L.r[0]=L.r[low]; //使用子表中第一个记录作为枢轴记录 privotkey=L.r[low].key; //枢轴记录关键字 while(i { while(i { if(L.r[j].key>L.r[j+1].key && j!=high) //加入起泡思想 { L.r[j].key= L.r[j].key+L.r[j+1].key; L.r[j+1].key=L.r[j].key-L.r[j+1].key; L.r[j].key= L.r[j].key-L.r[j+1].key; part.swap++; } j--; //指针j后退1个位置,进行下一次比较 } //while1 if(i==j) //最近的while1执行后,有可能导致i==j,即枢轴记录最终位置已确定 break; //当i==j成立时,应及时退出外层while循环 L.r[i]=L.r[j]; //否则即i if(L.r[i-1].key>L.r[i].key && i>low) //前置操作执行后,进行逆位序判断。i>low确保不会下溢出 { L.r[i-1].key=L.r[i-1].key+L.r[i].key; L.r[i].key=L.r[i-1].key-L.r[i].key; L.r[i-1].key=L.r[i-1].key-L.r[i].key; } i++; while(i { if(L.r[i-1].key>L.r[i].key && i!=low) //判断i处记录和i+1处记录之间是否逆序 { L.r[i-1].key= L.r[i-1].key+L.r[i].key; L.r[i].key=L.r[i-1].key-L.r[i].key; L.r[i-1].key= L.r[i-1].key-L.r[i].key; } i++; //指针i前移1个位置,进行下一次比较 } //while2从前往后扫描找比枢轴记录关键字大的记录 if(i==j) //最近的while2执行后,亦有可能导致i==j,即枢轴记录最终位置已确定 break; //当i==j成立时,应及时退出外层while循环 L.r[j]=L.r[i]; //执行后置操作 if(L.r[j].key>L.r[j+1].key && j { L.r[j].key= L.r[j].key+L.r[j+1].key; L.r[j+1].key=L.r[j].key-L.r[j+1].key; L.r[j].key= L.r[j].key-L.r[j+1].key; } j--; } //外层大while if(i==low && part.swap==0) //当待排序列已非递减有序,置划分标志为1 part.over=1; //此时置划分标志为1 else { L.r[i]=L.r[0]; //枢轴记录到位 part.pivotloc=i; //返回划分位置序号 } return part; //返回结构体变量part }//partition voidQuick_Sort(Sequence_List &L, int i, int j) { //对顺序表L中的子序列L.r[i...j]做快速排序 cout< //输出时增强递归程序的可读性 Part_loction part; if(i { part=partition(L,i,j); if(part.over) cout< else {Quick_Sort(L, i, part.pivotloc-1); //递归调用低子表部分 Quick_Sort(L, part.pivotloc+1, j); //递归调用高子表部分 } }//if }//QuickOnePass voidQ_Sort(Sequence_List &L) { //对顺序表L作快速排序 Quick_Sort(L, 1, L.length); }//Quick Sort void main() {clock_t start,ends; start= clock( ); Sequence_List L; L.length=2500; //原始待排序列长度 Initial_sequence(L); //根据原始待排序列长度初始化顺序表L cout<<"Please output the initial sequcence before quick sort:"< print_Sequence_List_L(L, 1, L.length); //输出待排记录初始序列 Q_Sort(L); //调用快排算法 cout< print_Sequence_List_L(L, 1, L.length); //输出快速排序后待排记录的非递减序列 ends = clock( ); cout < }//main 假如变量a、b同类型,则a=a+b,b=a-b,a=a-b;这三条语句即可实现a、b变量之间值的互换。同理上述源码中,消除逆位序时未使用中间变量。根据变量的特点,通过两个相邻记录关键字之间的加、减及赋值运算,实现两相邻记录关键字的互换。 算法2的改进工作使得指针i、j在移动过程中以及前置、后置执行后有效地消除了相邻记录关键字之间可能存在的逆位序,并且能及时判断待排序列是否已经非递减有序从而结束递归划分。但消除逆位序工作的同时也不可避免地增加了时间开销。在VC++6.0编译环境下采用srand(time(0))随机函数发生器产生随机数作为原始待排序列,同时采用clock( )函数来监测程序运行时间时发现,当产生的随机序列记录数小于500时,算法1和算符2运行时间均为0秒。但当随机样本数量逐步加剧时,算法2较算法1在时间性能上稍显逊色,以随机产生2 500个1 000以内的随机整数为例,运行30次后求得算法1的平均运行时间为0.484 s,而同等条件下算法2的平均运行时间为0.5 s。这表明改写后的算法2有效地消除了逆位序,从而在待排序列非递减有序时能及时退出划分,而算法运行时间代价并未显著增加,仍保持在O(n2)这一数量级。2 基于前置、后置方法实现快速排序一趟划分的改写算法及分析

3 改进后算法最坏情况下的性能分析

4 完整的代码描述
5 结语
