基于遗传算法的数控雕铣切削参数优化

□江灏源

云南机电职业技术学院 昆明 650203

随着科学技术的快速发展，全球制造业已经取得了长足进步，但在发展高速数控加工装备的同时，制造业依然普遍存在能源消耗大、环境效益差等问题。近年来，在全球气候变暖的大背景下，低能耗、低排放、低污染的绿色制造已经在世界各国掀起了热潮[1-2]。

数控雕铣属于数控加工的一种，其独有的加工特点解决了复杂微小曲面的加工精度问题，在电子产品、工艺产品等精细加工方面得到了广泛应用[3]。笔者针对目前数控雕铣过程中存在的能量耗损大、加工效率低等问题，通过改进遗传算法对数控雕铣的加工参数进行优化，得到与雕铣加工效率和碳排放量最优值对应的加工参数，有效解决了各大生产厂商在复杂曲面数控雕铣加工中遇到的加工效率低和成本高等难题，大大提升了厂商的生产效率，降低了加工成本，并实现了节能减排，增强了企业产品的综合竞争力。

1 切削优化建模

1.1 优化目标

在机械加工中解决加工参数优化问题，通常将企业的经济指标，如最大利润、最低成本和最高生产率中的一个或几个作为目标进行优化，同时构建相应的函数表达式，再结合实际加工过程来设定约束条件，并应用优化算法，在全局或局部进行求解，最终得出最优参数值。

数控雕铣的加工过程是非常复杂的，零件的加工质量受到很多因素影响。由于数控雕铣加工采用高的转速主轴和小径刀具，使数控雕铣过程存在加工效率低、能耗大、零件表面质量难以控制，以及环境污染严重等问题。这些问题之间并不独立，相互之间有很多关联性，所以在确定优化目标时，需要选择其中较为关键的几个重要因素作为目标函数。基于以上分析，以高效和低碳为优化目标，即以加工时间T、碳排放量C为优化对象。

2.2 以高效为目标的优化函数

在一个工序中，加工时间包括切削时间、辅助时间、换刀时间，这些时间受刀具耐用度、切削常数、刀具寿命[4]、零件加工要求等因素影响。综合以上因素，建立时间目标函数 ft（X）：

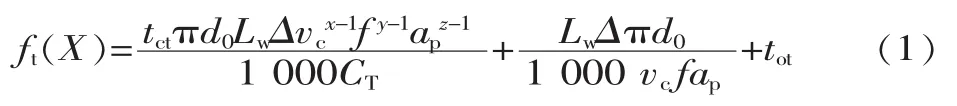
式中：tct为换刀时间；d0为模拟刀具直径；Lw为零件加工长度；Δ为加工余量；vc为切削速度；f为进给量；ap为背吃刀量；tot为辅助时间；CT为与切削条件有关的常数；x、y、z 为刀具寿命因数。

1.3 以低碳为目标的优化函数

在数控雕铣加工过程中，碳排放的来源一般有三类：加工消耗电能引起的碳排放、刀具磨损引起的碳排放、使用的切削液引起的碳排放。因此，碳排放量C表达式为：

式中：Ce为电能引起的碳排放量；Ct为刀具引起的碳排放量；Cc为切削液引起的碳排放量。

在引入相关参数后，得到碳排放目标函数fC（X）：

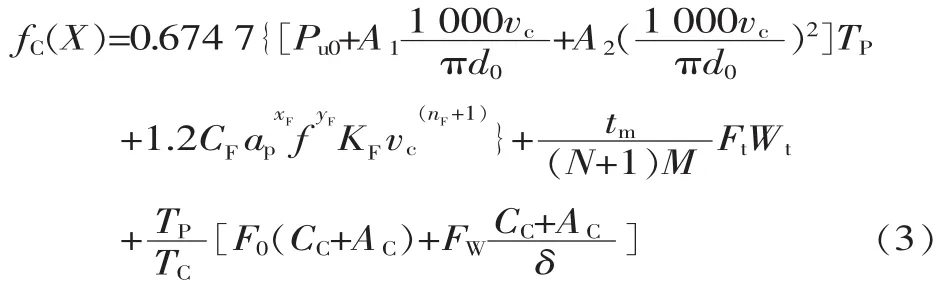
式中：Pu0为机床功率；TP为加工时间；tm为工序切削时间；N为刀具刃磨次数；M为刀具耐用度；Ft为刀具碳排放因数；Wt为刀具质量；TC为切削液更换周期；F0为纯矿物油排放因数；CC为初始切削液用量；AC为附加切削液用量；FW为废弃切削液排放因数；δ为切削液浓度；A1、A2、CF、xF、yF、nF、KF均为机床参数。

1.4 目标函数约束

在参数优化中，由于涉及对机加工机制的深入认知，以及对实际加工条件合理的简化表达，因此如何准确建立函数约束，一直以来都是相对复杂的问题。根据雕铣的铣削机制，在结合现场加工条件的基础上，建立几个约束条件[5]。

（1）主轴转速约束，即切削速度约束：

式中：Smin为机床主轴最低转速；Smax为机床主轴最高转速。

（2）进给量约束：

式中：fmin为机床最小进给量；fmax为机床最大进给量。

（3）切削力约束：

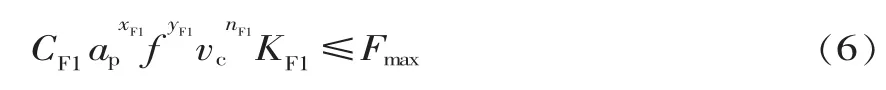
式中：Fmax为机床允许的最大进给力；KF1、CF1、nF1、xF1、yF1均为机床参数，可由切削用量手册查得[6]。

（4）功率约束。机床功率P为：

式中：Fc为切削力。

要求在切削加工时所消耗的功率Pc不能超过机床输出的最大功率，即：

式中：η为机床功率有效因数；Pmax为机床最大有效功率。

（5）加工质量约束，即表面粗糙度约束。根据文献[7]，零件加工后的表面粗糙度Ra要求为：

式中：rε为刀尖圆弧半径；Ramax为零件表面粗糙度最大允许值。

将以上优化目标和约束条件代入式（1）和式（3），可建立目标函数和约束条件：

模拟加工所用材料为2024铝合金，切削深度为0.06 mm，测得的换刀时间为0.5 min，辅助时间为0.8 min。查阅切削用量手册，得到优化目标函数中各参数：CT=145，x=5，y=1.75，z=0.75，CF1=2 880，KF1=1，nF1=-0.4，xF1=1.0，yF1=0.5，A1=0.227，A2=0.667×10-6，xF=1，yF=0.8，nF=-0.2，CF=2 700，KF=0.5，δ=5%， Fw=0.2，Ft=29.6，η=0.8，Pu0=40.6 kW，Pmax=15 kW，N=1，AC=4.5 L，CL=8.7 L，Fmax=9 000 N，F0=2.85，Wt=15 g，rε=0.8 mm，fmin=0，fmax=6 mm/min，Smin=3 000 r/min，Smax=28 000 r/min，Ramax=6.4 μm。此外，TC为两个月。

将各参数代入式（1）和式（3），得到简化的目标函数和约束条件：

至此，结合实际切削参数和切削用量手册将约束条件设置好，并换算出了具体数值，为下一步进行具体优化做好了铺垫。

2 基于传统遗传算法的切削参数优化

常用的优化算法有遗传算法、人工神经网络算法、人工蜂群算法、蚁群算法、模拟退火算法等，各种算法又可互相结合进行优化互补。

与常规寻优算法相比，遗传算法有如下特点[8]：

（1）运算对象是决策变量的编码；

（2）直接以目标函数值作为搜索信息；

（3）同时使用多个搜索点的搜索信息，具有隐含并行性；

（4）使用概率搜索技术取代非确定性规则；

（5）具有强大的容错能力。

2.1 以高效为目标求解

基于MATLAB遗传算法工具包，完成切削参数优化[9]。

步骤一，简化目标函数。高效目标函数为式（1），经查阅切削用量手册，得到简化的目标函数，只包含进给量和切削速度两个变量。

步骤二，编写优化函数的.m格式文件T_ft（x）.m。使用遗传工具包编写一个.m格式文件，来确定需要优化的函数。此文件包含一个行向量，其长度为优化函数中独立变量的个数，还需返回一个标量，这个标量就是优化函数的函数值。

步骤三，简化约束条件。根据前文，查阅切削用量手册，可得简化后的约束条件为753.6≤vc≤7 033.6，0≤f≤6，f0.5vc-0.4≤0.025 6，f0.5vc0.6≤52 083.33，f2≤164.1。

步骤四，编写约束条件的.m格式文件T_cc（x）.m。

步骤五，设置约束边界值。

步骤六，设置遗传算法的参数。设置迭代次数缺省值为100。

步骤七，运行求解。点击RUN键，遗传算法工具包开始迭代，待寻得最优解后，输出求解结果，此时vc=6 865.305 mm/min，f=1 030 mm/min，通过目标函数计算得到 T=801 s，C=2.213 g。

2.2 以低碳为目标求解

以低碳为目标求解和以高效为目标求解的不同之处仅在于目标函数不同，而约束条件都是一样的。更改目标函数为碳排放量函数，编写目标函数的.m格式文件 C_fc（x）.m。

按照同样的步骤，可以求得以低碳为目标的最优解，此时 vc=3 895.49 m/min，f=1 252 mm/min，通过目标函数计算得到T=3 056 s，C=0.385 g。

2.3 以高效低碳为目标的最优化

图1所示为两个典型人物浮雕工艺品，其曲面加工外形尺寸为 φ80 mm×3 mm。曲面具有图案复杂、造型精细的特点，通常采用数控雕铣技术来进行加工。

▲图1 浮雕工艺品

加工技术要求如下：

（1）加工后的工件表面粗糙度Ra≤6.4 μm；

（2）加工表面应具有较好的光泽度，避免出现走刀痕迹，以及较为明显的马赛克痕迹；

仿真加工前进行一系列准备工作。

（1）加工设备使用数控雕铣机。

（2）毛坯尺寸为 φ80 mm×10 mm。

（3）毛坯材料为铝合金。

（4）工装夹具为高精密四爪卡盘。

（5）走刀方式应最大程度保证雕铣加工质量，考虑浮雕曲面曲率复杂、陡壁多等特点，设置走刀方式为角度为0°的平行截线走刀。

（6）背吃刀量为0.06 mm。

（7）加工余量为0.09 mm。

（8）选用φ2 mm整体式两刃钨钢球头立铣刀进行精加工，这一刀具的具体规格为φ2 mm×4 mm×14 mm ×51 mm。

（9）浮雕工艺品的曲面复杂度为0.642 4 mm。

仿真加工共设计了四组优化方案，见表1。对切削参数优化模型的可行性进行验证，建立以时间和碳排放量为优化目标的两个函数，分别改变方案中主轴转速S与进给量f，进行仿真加工。

按照步骤进行优化求解，分别计算得到四组方案对应的结果：方案 1中 T=4 416 s，C=1.937 3 g，Ra=0.901 8 μm； 方案 2 中 T=2 561 s，C=0.928 3 g，Ra=0.953 3 μm； 方案 3 中 T=4 470 s，C=1.799 9 g，Ra=0.977 6 μm； 方案 4 中 T=2 336 s，C=0.964 6 g，Ra=1.019 5 μm。

表1 仿真加工优化方案

3 基于改进遗传算法的切削参数优化

3.1 改进遗传算法的形成

传统遗传算法的搜索速度很快，可以在较短时间内快速到达最优值附近区域，但如果想要在该区域进行解的收敛以求出最优解，所需要的时间却很长，在很大程度上降低了寻优效率，因此必须对传统遗传算法进行改进。笔者的改进思路是以传统遗传算法为基础，引入模拟退火算法的思想和算子，形成一个新的改进算法。

模拟退火算法具有以一定概率接受不理想状态目标函数的特性，即算法的走向具有一定的概率性，有可能会走向好的方向，也有可能会走向差的方向。这种走向的不确定性在一定程度上保证了算法在寻优过程中即使陷入局部最优，只要经过足够长的时间，也可以跳出局部收敛，从而得到全局收敛最优解。在具体操作中，通常并不一定要找寻最优解，而是只要求出一个满意的近似最优解即可。笔者正是基于此对传统遗传算法进行改进。

在具体算法流程中，改进遗传算法与传统遗传算法相似，在进行交叉运算之后，系统随机产生与初始种群个数相同的解，之后和交叉运算后的解一起，通过米特罗波利斯法则选择新的多样化种群，进入下一个流程。

3.2 切削参数优化

由于在传统遗传算法的寻优求解过程中，父代个体在遗传、交叉和变异过程中所产生的某些子代适应度值会急剧下降，这种情况是不可避免的，这些子代个体就是所谓的差解。此时，为了保证种群的多样化特性，差解不能全盘舍弃，而是根据米特罗波利斯法则设定一个概率以接受差解，这样可以有效防止算法陷入局部最优[10-12]。受到软件功能的限制，传统遗传算法工具包无法直接使用改进遗传算法，所以必须事先按算法的操作步骤编写MATLAB程序代码，形成.m格式文件。

两种遗传算法的比较如图2所示，由图2可以看出，改进遗传算法所用总时间与传统遗传算法时间相差不多，只是变化比较平稳。

由于在优化时目标函数优化目标具有不同的侧重点，因此对应得到两种优化过程，即分别以高效和低碳为优化目标，优化结果见表2。

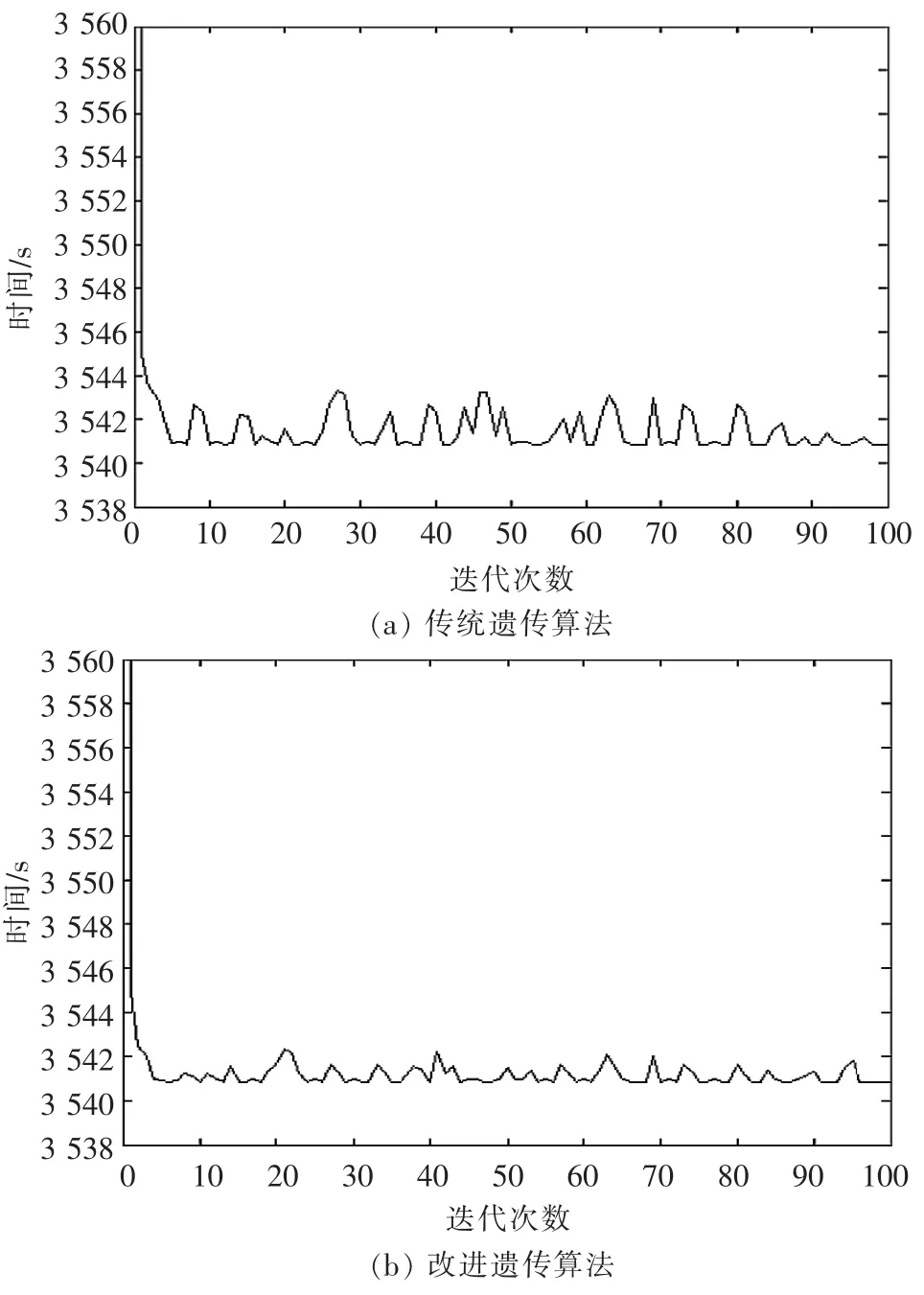
▲图2 遗传算法比较

表2 改进遗传算法优化结果

由表2可知：以高效为主要优化目标时，切削速度较快，刀具磨损较大，进而导致刀具碳排放量较大；以低碳为主要优化目标时，切削速度相对较慢，刀具磨损较小，刀具碳排放量也较小。可见，切削参数优化对制造企业实施低碳制造具有重要意义。

改进遗传算法相对于传统遗传算法的优势，在于在过程中应用米特罗波利斯法则后可以使算法快速跳出局部最优，达到全局最优，从而增强了算法的稳定性，使算法更高效。

4 总结

笔者以数控雕铣加工过程为研究对象，针对其在加工过程中存在能耗高、加工效率低、环境污染严重等问题，综合考虑数控雕铣加工过程中机床设备性能，在加工实际约束条件的基础上，建立目标优化数学模型，获得主轴转速和进给速度的最优值，实现了最短加工时间和最少碳排放量的优化目标。分别通过传统遗传算法和改进遗传算法以加工时间和碳排放量为优化目标进行了优化，通过模拟加工验证了算法的可行性。对优化结果进行对比分析，确认改进遗传算法相比传统遗传算法在全局最优解问题上更具有优越性。