货车车架多目标拓扑优化*

□戎飞 □刘胜

上海工程技术大学机械工程学院 上海 201620

1 研究背景

随着全球汽车数量的急剧上升，汽车尾气排放成为霾现象的重要原因，如要发展健康环保的汽车，则必须解决汽车尾气排放问题。研究表明，汽车质量每减轻10%，燃油消耗可减少 6%～8%，尾气排放减少 4%[1]。根据国内外的发展方向，解决汽车环保问题的主要方法有两种——研发新能源汽车、发展汽车轻量化技术。在新能源汽车还未普及的情况下，汽车轻量化技术必然是值得关注的发展方向[2-4]。

车架是汽车中的重要部件，承载着车身、动力总成、驾驶室、货物和其它所有零部件的质量，同时承受行驶过程中来自路面的冲击、扭曲、惯性力、振动等。通常，车架质量占汽车总质量的相当大比重，因此被认为是汽车的核心部件之一。

拓扑优化分为离散体结构拓扑优化和连续体结构拓扑优化[5]，目前，连续体拓扑优化主要集中在单目标拓扑优化问题上，有关车架拓扑优化也是单目标拓扑优化问题。但是，在实际工程应用中存在很多多目标拓扑优化问题，单目标拓扑优化很难满足设计要求。笔者以货车车架为研究对象，建立了基于固体各向同性材料惩罚模型材料密度插值法的多目标拓扑优化数学模型，应用HyperWorks有限元软件中的Optistruct拓扑优化模块，得到同时满足静态多工况下柔度最小及低阶模态最大要求的车架拓扑结构[6-8]。

2 车架静动态分析

2.1 静态分析

按照车架实际尺寸，在UG NX 8.5软件中建立车架的三维结构模型，然后将三维模型导入Hypermesh软件中进行前处理，网格大小按整车网格标准划分，通常为10 mm。载荷按简化方法施加，将货箱与货物的质量以均布载荷的方式施加到相应位置，车架自重通过定义重力卡片中的重力加速度来施加，其它各总成质量等效为集中载荷的形式施加在对应位置。约束作用于车架与悬架的连接处，前处理模型如图1所示。

完成上述设定后，对车架进行静态分析，得到车架的应力与应变云图，分别如图2、图3所示。最大应力产生于第三根曲梁与纵梁的连接处，因为此处受到了油箱的集中载荷及货物与货箱的均布载荷，所以应力最大，与实际情况相符合。最大应变发生在车架的中部和后部，因为中后部承载了整个车厢和货物的质量，所以变形较大，与实际情况相符合。

▲图1 车架前处理模型

2.2 动态分析

对车架进行模态分析，因为高阶模态对结构振动的影响微乎其微，没有必要关注高阶模态，所以笔者只从提取频率中找出如图4所示的低阶模态。在实际工程中，只需关注一阶弯曲、一阶扭转、二阶弯曲、二阶扭转，以及它们的组合，更高阶的可不予考虑。

2.3 静动态分析结果

由车架静态分析可知，最大应力为339 MPa，车架质量为868 kg，最大应变为1.887 mm。基于车架动态分析，从提取的所有频率中提取前六阶频率及振型，见表1。

3 多目标拓扑优化数学模型

多目标拓扑优化问题求解一般有两种方法[9]：一种是直接得到非劣解，然后从这些解中选择出最符合优化目标的解；另一种是构造一个新函数，将多目标转化为单目标进行求解。第二种方法主要有理想点法、功效系数法和线性加权法等。

3.1 静刚度拓扑优化数学模型

▲图2 车架应力云图

▲图3 车架应变云图

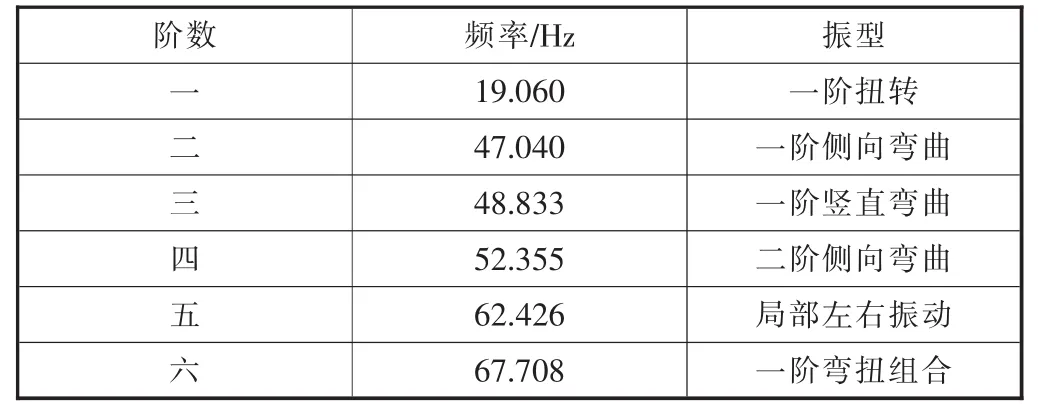
表1 车架低阶频率及振型

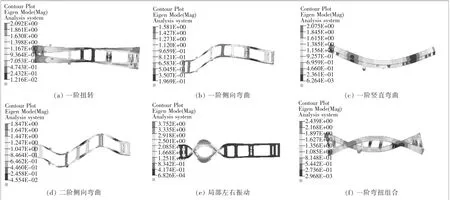
▲图4 车架低阶模态

在拓扑优化中，通常将刚度最大化的问题转化为柔度最小化的问题进行拓扑优化。以体积分数为约束，以柔度最小化为目标函数，建立车架静态刚度拓扑优化模型：

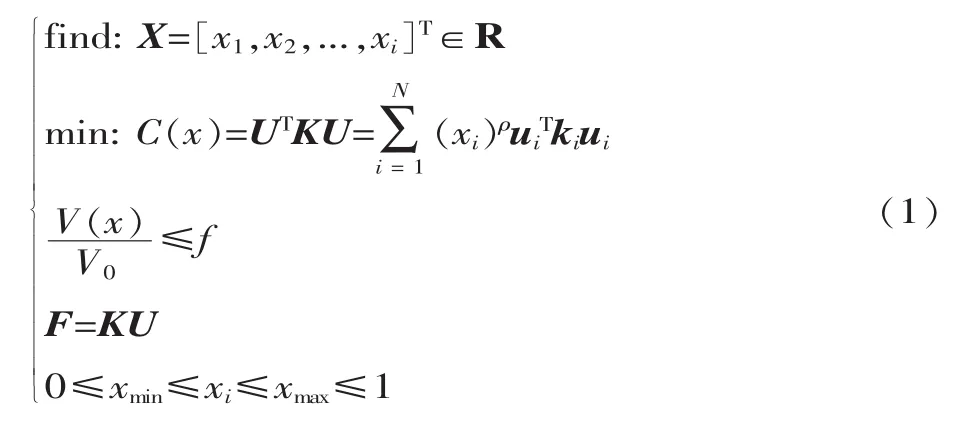
式中：C（x）为结构柔度；xi为第 i个单元的设计变量，i=1，2，3，...，N，N 为设计变量总数；ρ为惩罚因子；ui为单元位移矩阵；ki为单元刚度矩阵；V （x）为结构有效体积；V0为结构原体积；f为体积分数；F为载荷矩阵；U为位移矩阵；K为刚度矩阵。

3.2 振动频率拓扑优化模型

通常在动态频率拓扑优化时将结构体积分数作为约束，将几个重要的低阶频率最大作为目标。在优化过程中，由于材料的修改，当一个阶次的频率最大时，其它阶次频率会降到一个较小的值，而且会出现互相交换，即模态交换[10]，这样就会使得结果不准确。为了避免产生这种现象，笔者采用平均频率公式来定义固有频率拓扑优化数学模型：

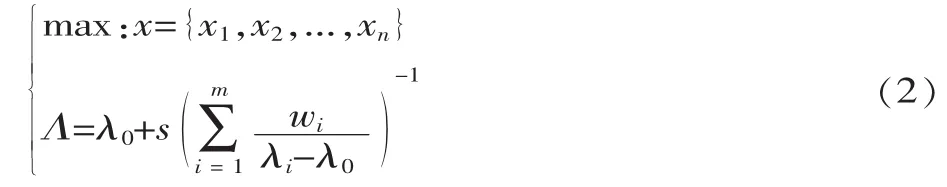
式中：Λ 为平均频率；λi为第 i阶特征频率；λ0、s为给定参数；wi为第i阶频率因子；m为提取的低阶频率阶次个数，m=6。

3.3 车架多目标拓扑优化数学模型

同样以体积分数作为多目标拓扑优化的约束，将车架静态多个单工况目标与动态振动频率目标通过折中规划法[11]糅合为一个单目标函数：

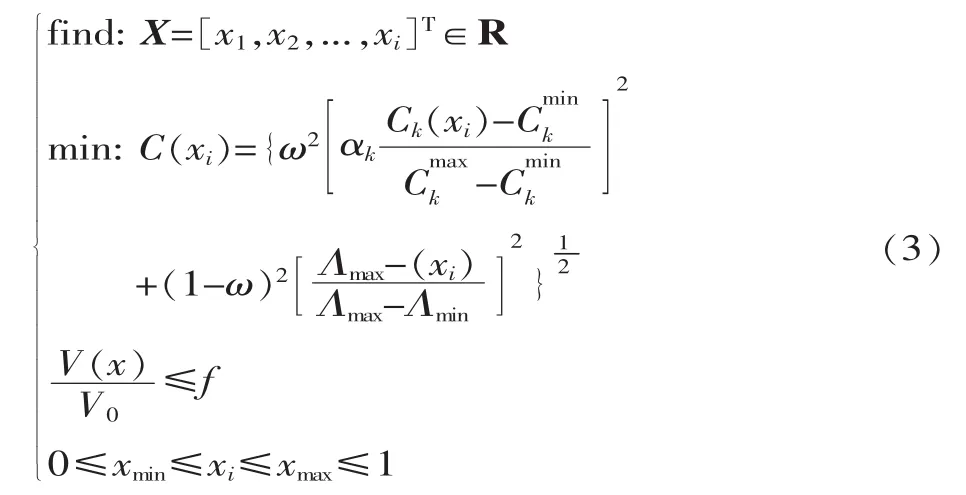
式中：k=1代表弯曲工况，k=2代表前扭转工况，k=3代表后扭转工况；分别为对应工况下的结构柔度最大、最小值；αk为各静态单目标所占权重因子，根据实际工程经验取 α1=0.2，α2=0.4，α3=0.4；ω 为柔度目标函数权重，ω=0.6。

4 拓扑优化过程及结果

拓扑优化时首先要先建立一个6 937 mm×850 mm×244 mm的长方体，由于模型是等厚度的，因此在Hypermesh软件中对整个模型抽取中面，简化复杂程度和计算量。纵梁为非设计区域，只有横梁部分是设计区域，按前述方法对模型进行前处理。

4.1 拓扑优化过程

完成所有的前处理设置后，在Optistruct模块中，通过调用Optimization模块的Dequation功能，定义车架多目标拓扑优化的数学模型，然后将定义的函数与体积作为响应，最后将体积响应作为约束，体积上限为30%，将函数响应作为目标函数，通过拓扑优化得到车架拓扑结构。

将固体各向同性材料惩罚模型材料密度插值法与折中规划法相结合进行迭代求解，得到车架拓扑密度云图，如图5所示。

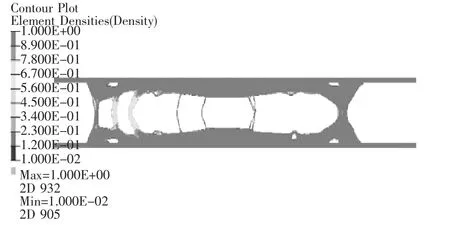
▲图5 车架拓扑密度云图

4.2 拓扑优化结果

拓扑优化得到的车架结构只是一个设计的初始改良型方案，并不能直接应用。在拓扑优化的基础上，通过对拓扑结果进行分析，构造出优化后车架模型[12]，如图6所示。

▲图6 优化后车架模型

根据原车架施加的载荷与约束条件，对新车架同样施加载荷与约束条件，并进行静动态分析，得到优化后车架的应力、应变云图，分别如图7、图8所示，低阶频率见表2。优化前后车架结构性能对比见表3。

5 结论

基于固体各向同性材料惩罚模型材料密度插值法与折中规划法，建立货车车架多目标拓扑优化数学模型，实现了车架的多目标优化。经过拓扑优化后车架的最大应力和最大应变均比原车架有所减小，车架结构刚度提高。在模态分析中，低阶频率都有一定的提高，减少了在低频环境中的共振现象。重构车架质量减轻了17.8%，使车架使用的材料更少。可见，笔者所用方法对实际工程有参考价值。

▲图7 优化后车架应力云图

▲图8 优化后车架应变云图

表2 优化后车架低阶频率

表3 优化前后车架结构性能