基于IPSO_LSSVM的电力电容器噪声测量结果的不确定度评定
2018-07-25张华伟
张华伟
山东艺术学院,山东 济南 250001
电力电容器单元噪声声功率级的测量过程是信息科学采集的过程,测量过程中会受到很多因素的影响,如何科学正确地分析和评定电力电容器单元噪声声功率级的测量结果的不确定度,对提高电力电容器单元噪声声功率级测量的准确度和正确评价电力电容器的噪声具有重要的理论价值和现实意义[1]。
测量不确定度主要用来说明测量结果的可信程度,通常用标准偏差进行表征。GUM中的不确定度评定方法具有计算量大、过程繁琐、相关限制多、操作性较差的缺点,给现实中的不确定度评定带来了诸多不便[2,3]。最小二乘支持向量机[4]是一种基于统计学的机器学习算法,由于其优越的非线性映射能力,目前被广泛地应用于模式识别[5]、目标定位[6]、回归预测[7]和分类预测[8]等方面。然而尚未发现将LSSVM应用于不确定评定的文献,本文针对LSSVM模型结果易受参数c和σ的影响,运用改进的粒子群算法(IPSO)优化LSSVM模型,并将其应用于电力电容器单元噪声测量结果的不确定评定,研究结果表明,本文提出的算法具有精度高、速度快的优点。
1 改进的PSO算法
1.1 PSO算法
PSO算法(Particle Swarm Optimization Algorithm,PSO)主要通过粒子群群体之间的协作和竞争实现最优化搜索[9],其速度和位置更新策略如下:

其中,vid(t)和xid(t)分别表示在t时刻时第i粒子的速度和位置;c1、c2分别为学习因子。
1.2 改进的粒子群算法
为提高PSO的收敛速度和避免陷入局部最优的问题,提出一种基于随机搜索因子改进的粒子群算法,改进策略如下:

其中,公式(4)保证粒子在搜索范围内寻优;公式(5)主要改善局部搜索能力和全局搜索能力;a改进粒子的分布方式。
2 最小二乘支持向量机
若有m个训练样本为输入向量,iy∈R为输出向量,LSSVM数学模型表示为:

其中,ω为权重;C为LSSVM的惩罚参数;ζi为LSSVM的松弛变量;φ(x)为空间映射函数;b为LSSVM的偏差。在此基础上,LSSVM的lagrange函数L可表示为[10]:
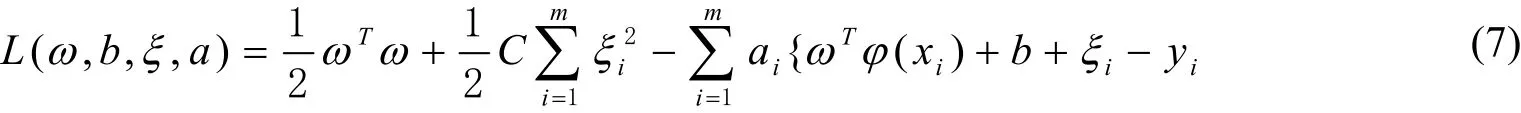
其中,ai表示lagrange乘子。对公式(7)求偏导[11]:
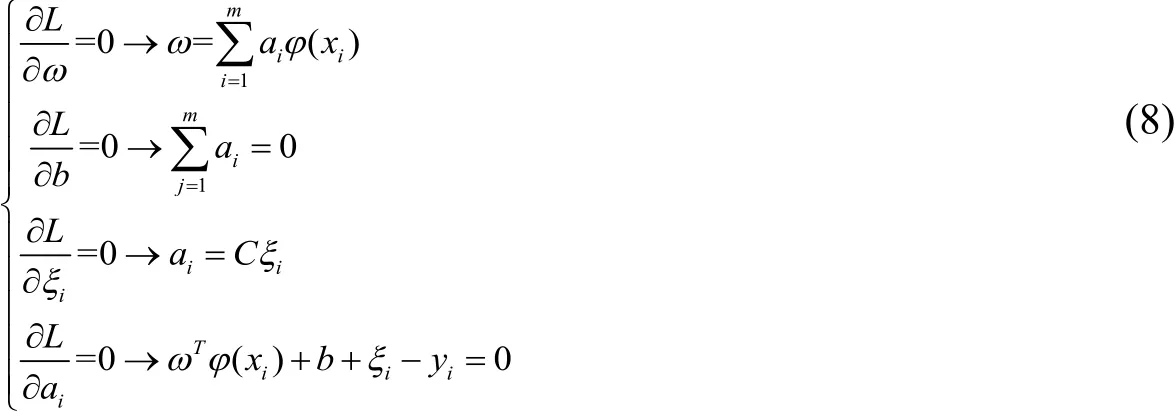
消去ω和ζi,可得如下公式:

其中,Q=(1,…,1)T,A=(a1,a2,…,am)T,Y=(y1,y2,…,ym)T,通过求解公式(9),可得到LSSVM模型的估计公式,其如下所示:

3 不确定度数学模型
测量不确定度主要用来表征测量结果的可信程度,一般采用标准偏差的形式表示。测量不确定度评定主要是建立影响量x和被测量Y的数学关系模型[12]:
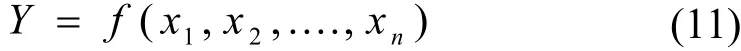
电力电容器噪声测量结果的不确定度影响分量主要包括x1时间平均声压级均值,x2测量面积,x3背景噪声修正,x4分贝基准修正,x5声辐射阻抗修正,x6环境反射,x7声级计,x8样本点数,x9角度修正,x10测量方法等引入的不确定分量。基于LSSVM的电力电容器噪声测量结果的不确定度评定结构示意图如图1所示。
图1中,输入为电力电容器单元噪声测量结果的影响因素,输出为电力电容器单元噪声测量值,通过LSSVM模型构建出电力电容器单元噪声测量结果的不确定度评定模型,建立影响因素和噪声测量值之间的映射关系。
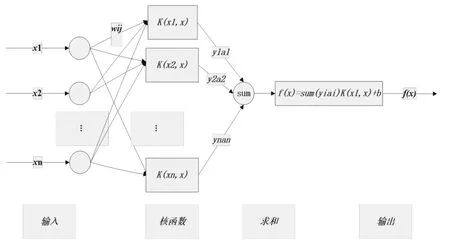
图1 LSSVM噪声测量结果的不确定评定示意图Fig.1 Schematic diagram of uncertainty evaluation of noise measurement results of LSSVM
4 基于IPSO_LSSVM的不确定评定
为了使得电力电容器单元噪声测量不确定评定结果最优,选择噪声测量不确定度评定的均方根误差作为适应度函数,通过IPSO算法实现LSSVM模型参数的最优化选择。

Step1:归一化电力电容器单元噪声测量结果不确定的样本数据(影响因素和被测量),并样本数据划分为训练集样本与测试集样本;
Step2:种群和参数初始化,IPSO算法的学习因子为c1、c2,最大进化代数为maxgen,种群规模为popsize;
Step3:计算每个粒子个体的适应度;
Step4:更新粒子的位置和速度;
Step5:重新计算和评估每个粒子个体的适应度;
Step6:若当前迭代次数gen>maxgen,IPSO算法满足终止条件并停止寻优,输出寻优结果;否则gen=gen+1,转到Step4;
Step7:输出惩罚函数C和核函数σ的最优参数值,并实现电力电容器单元噪声测量结果的不确定度评定。
5 实证分析
5.1 评价指标
选择平均绝对百分比误差MAPE、平均绝对误差MAE和均方根误差RMSE作为电力电容器单元噪声测量结果的不确定度评定结果好坏的评价指标:

其中,yi表示某一样本数据的不确定实际值;表示某一样本数据的不确定评定值,N表示评定样本的数量。
5.2 实验结果
将电力电容器单元噪声测量结果的不确定度样本数据划分成训练集样本和测试集样本,分别用于建立模型和验证模型。训练集样本数据97组,测试集样本44组,IPS0算法参数设定为:最大进化代数为maxgen=100,种群规模为popsize=20,学习因子c1=c2=0.5,评定结果如图2所示。
为了证明本文算法IPSO_LSSVM进行电力电容器单元噪声测量结果的不确定度评定的优越性,将其与PSO_LSSVM[13]、GA_LSSVM[14]、DE_LSSVM[15]和LSSVM进行对比,不同算法的预测结果如图3~6所示,对比结果如表1所示。
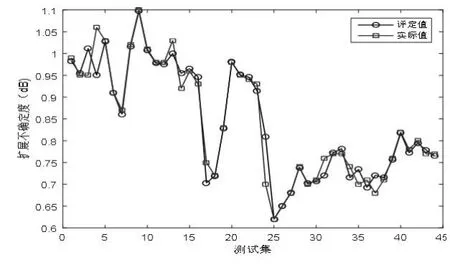
图2 IPSO_LSSVM评定结果Fig.2IPSO_LSSVMevaluationresults

图3 PSO_LSSVM评定结果Fig.3PSO_LSSVM evaluation results
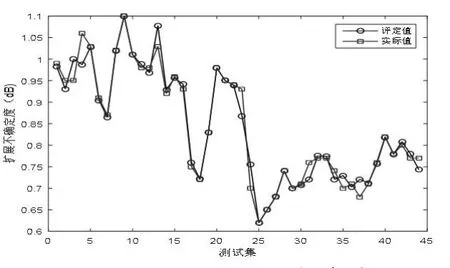
图4 GA_LSSVM评定结果Fig.4GA_LSSVM evaluation results
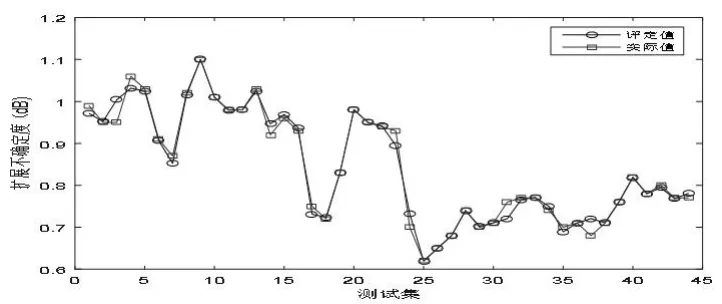
图5 DE_LSSVM评定结果Fig.5 DE_LSSVM evaluation results

图6 LSSVM评定结果Fig.6 LSSVM evaluation results

表1 不同算法不确定度评定结果对比Table 1 Comparison of uncertainty evaluation results of different algorithms
结合图3~6和表1不同算法进行电力电容器单元噪声测量结果的不确定度评定结果可知,在RMSE、MAE和MAPE三个评价指标上,与PSO_LSSVM、GA_LSSVM、DE_LSSVM和LSSVM相比较,IPSO_LSSVM具有更高的预测精度;其次,GA_LSSVM的预测精度优于PSO_LSSVM、DE_LSSVM和LSSVM;最后,LSSVM的预测精度最差,RMSE、MAE和MAPE分别比IPSO_LSSVM低0.5032、0.4421和5.1042%,通过对比可知,运用群智能算法对LSSVM模型的惩罚函数C和核函数σ进行优化,可以有效提高LSSVM的预测精度,其中IPSO算法对LSSVM的优化效果最好,从而验证本文算法的可靠性和有效性,可以进行推广应用。
6 结 论
本文将LSSVM算法引入电力电容器单元噪声测量不确定评定,通过将噪声测量的影响因素作为LSSVM输入,扩展不确定度作为LSSVM输出,建立LSSVM噪声测量的不确定评定数学模型。针对LSSVM模型结果易受参数C和σ的影响,运用改进的粒子群算法(IPSO)优化LSSVM模型,并将其应用于电力电容器单元噪声测量结果的不确定评定,研究结果表明,本文提出的算法具有精度高、速度快的优点,有利于在现实中测量不确定度评定的应用和推广。
