基于坐标分割的聚集型代数多重网格预条件研究

吴建平 银福康 彭 军 杨锦辉

(国防科学技术大学海洋科学与工程研究院 湖南 长沙 410073)

0 引 言

稀疏线性方程组是混凝土细观数值模拟[1]、数值天气预报格点模式[2]、线性弹性问题[3]、油藏模拟[4]等许多科学与工程计算领域的核心计算模块之一，求解时间在整个应用问题中占很大比重，其求解效率是影响整个应用问题数值模拟效率的关键环节之一。正因为具有极端重要性，因此，直到最近，还广受关注并有大量研究[5-6]。Krylov子空间迭代[7-8]是求解这种稀疏线性方程组最有效而健壮的一般性方法之一，当系数矩阵对称正定时，其中共轭斜量(CG)法以计算经济、理论上较快的收敛速度应用最为广泛。但这种迭代法的实际收敛速度与系数矩阵的特征值分布有关，分布越集中，收敛速度越快。

多重网格算法[9-10]是求解稀疏线性方程组的另一类有效方法，其显著特点是通过将光滑与校正有机结合，具有潜在的快速收敛性。但这类方法健壮性一般不理想，因此，将其用作预条件，来加速Krylov子空间迭代法，是将两者优势有机结合的最佳选择。在针对一般稀疏线性方程组的代数多重网格算法中，聚集型代数多重网格算法以其计算与存储上的经济性、可控性广受关注。对这种多重网格算法，其核心是网格层次结构的选取与确定方法[11]，经典的聚集算法中，最有效的是基于强连接的算法及其变种[12-13]，但这些算法主要基于系数矩阵邻接图的局部特性，因而具有容易陷入局部最优的潜在缺陷，且不易于进行并行实现。文献[14]对多种聚集算法进行了比较，发现基于强连接的算法及其变种一般具有优势。文献[15]中提出了一种以图分割为基础的自顶向下型聚集构造算法，有效克服了这些问题。当已知线性方程组每个未知量对应的坐标时，利用坐标分割可以更快速地进行邻接图的分割，从而减少设置阶段所需要的时间。已有实验结果表明，这种算法相对于基于强连接的经典聚集算法，无论在计算效率，还是参数敏感性与健壮性方面，都具有明显优势。

1 基于坐标分割的多重网格预条件

考虑下述稀疏线性方程组：

Ax=b

(1)

式中：A是已知的对称正定稀疏矩阵，b为已知右端向量，x为待求的未知解向量。对式(1)，可以采用预条件CG法进行求解。采用预条件的目的是希望将式(1)化为另一个具有同解、且系数矩阵特征值分布更集中的线性方程组，同时应使得其中牵涉到的辅助计算量比较少。从这个意义上说，对A左乘或右乘一个近似逆矩阵是可行之道，这在辅助计算时又相当于近似求解式(1)，因此，任何近似求解式(1)的方法都可以作为预条件。多重网格型算法具有潜在最优收敛性，自然是用于式(1)的有效预条件选择之一。

聚集型代数多重网格具有存储与计算上的经济性，且易于控制，因而广受关注。聚集构造是这种算法的核心问题之一。在文献[8]中提出了一种自顶向下构建聚集与网格层次结构的方法，该方法的核心思想是从对应于A的邻接图G出发，先利用图分割算法，在要求子图之间连接边的边权之和最小的约束条件下，将G分为多个子图，使得各个子图中节点个数基本相当。之后，可以直接将每个子图中的节点聚集为一个点，从而形成最粗的网格层。

为构建其他网格层，可以先从最粗层中每个点对应的子图出发，将每个子图又按类似方式分为多个子图。这样，如果假设每次分为p个子图，则从最粗层开始，每细化一层，该层中对应的子图个数都增加到上一层的p倍。之后，每一层中的每个子图就自然形成一个聚集。按照所要求的条件，在进行图分割时，将使得子图之间连接边的边权之和最小，因而可以一定程度上确保子图之间的依赖关系较小。这与强连接的意义相近，将连接关系较强的节点尽量聚集在一起。但在此时以自顶向下的方式进行的，这与基于强连接的经典聚集算法具有本质上的不同，经典聚集算法是从局部搜索出发，对强连接的节点进行聚集。

由于基于图分割的聚集算法需要反复用到图分割算法，如果完全按照使得子图之间的连接边权之和最小的要求来进行图分割，将会导致设置阶段时间相当慢长。因此，只能采用启发式算法。对一般的图，可以采用MeTis 等软件包进行图的分割。但已有实践表明，采用这种图分割软件进行分割时，可能导致某些子图不连通。而对不连通结点进行聚集，从根本上与强连接的思想相违背，本质上将会导致多重网格算法性能的下降。因此，如何进行既能确保高效实现，又能确保子图连通性的图分割，是确保这种聚集型代数多重网格算法有效性的核心问题。

幸运的是，目前所求解的很多稀疏线性方程组，其来源多是大规模科学与工程计算。有的来源于偏微分方程数值求解，例如数值天气预报的格点模式等应用问题，是基于空间网格点进行离散所得到的。有的虽然不是来源于微分方程，但也基于空间网格点进行离散计算，例如混凝土细观数值模拟等结构力学中所得到的稀疏线性方程组就是典型例子。对这些稀疏线性方程组，每个未知量所对应的空间坐标已知，如果充分利用这种已知信息，可以进行既高效又确保连通性的图分割算法设计。

2 三种基于坐标的高效图分割算法

考虑无向图G=(V,E)，其中V={1,2,…,n}，E为连接边集合，假设V中结点i对应的坐标为(xi,yi,zi)，现在需要将其分割为p个子图。本节对这一问题，给出正方分割、最小界面分割与逐步单向分割等三种分割算法及其高效实现。

正方分割算法以每个子图接近于正方体或正方形的方式进行分割。在该算法中，先找出不同x、y、z坐标的个数，分别记为nxs、nys、nzs，并记下每个x、y、z坐标出现的次数，第i个x坐标出现的次数记为ixs(i)，第j个y坐标出现的次数记为iys(j)，第k个z坐标出现的次数记为izs(k)。为进行高效实现，先采用归并排序将所有结点按照x坐标优先、再y坐标优先、后z坐标优先的顺序，与坐标从小到大的顺序进行排序，每个结点对应的坐标相应进行调整。之后，分别从x、y、z三个方向，通过二分查找的方式，从已排序序列中找出每个方向上不同坐标的个数，并记录下该方向每个坐标出现的次数。以y方向为例，对排序后的结点依次进行扫描，先置nys=1，并将iys(1)置为第一个结点的y坐标，之后，对每个新结点，查找其对应y坐标在iys(1)到iys(nys)是否存在，如果不存在，则nys加1，并置iys(nys)等于该y坐标。

在进行图分割时，按尽量使得每个子图中的结点形成近似正方体或正方形的方式来进行组织。对三维问题，即当nzs=1时，按子图接近于正方形的方式进行分割，否则按子图接近于正方体的方式进行分割。这样可以最大程度上减少各子图之间的连接边数量。设将G分为p=px×py×pz个子图，在这种方式下，即尽量使得nxs:px=nys:py=nzs:pz，并尽量使得各方向上的坐标在该方向的分割中进行平均分布。

最小界面分割算法遍历所有可能的分割，并以每个子图表面积或周长之和最小的方式进行实际分割。在该算法中，先采用与正方分割类似的方式，找出不同坐标的个数，以及每个坐标出现的次数。再确定在分割数各种形式的分解p=px×py×pz中，哪一种最优。这里确定分割组织的方式与正方分割不同，是通过因数分解，使得每个子图表面积(三维情形)或周长(二维情形)总和最小。具体地，先将p进行因素分解，由此可以确定px、py、pz的各种不同组合形式，之后，对每种组合形式，在二维情况下可以计算每个子图的周长之和，在三维情况下，可以计算每个子图的表面积之和，最后采用使得总和最小的组合方式作为最终的分割组织形式。

逐步单向分割算法基于分割数的素因子分解，按素因子从大到小的顺序，每次沿不同坐标数最大的方向进行分割，直到所有素因子遍历完为止。在该算法中，先对p进行因数分解，并对各素因子按从大到小的顺序进行排序，之后，对G先按第一个素因子进行分割，并对分割所得子图，再按第二个素因子进行第二层分割，如此继续，直到所有素因子访问完毕为止。在对某个子图按照某个素因子进行分割时，按照与正方分割中相同的方式找出每个方向上的不同坐标个数，之后，分割沿先坐标个数最大、再坐标个数其次、最后坐标个数最小的优先顺序进行。因此，在进行每次分割之前，也需要进行排序，这依然采用归并排序来实现。这里，对p的所有素因子按从大到小的顺序进行排序，并依次进行分割，是为了确保最后分割所得每个子图中拥有尽可能相等的结点个数，这在多重网格算法构造中，有利于每层中每个子图中的结点数最大程度地相等，从而最终有利于确保多重网格算法的有效性。

3 数值实验

本文实验平台中的处理器为Intel(R) Xeon(R) CPU E5-4640 0 @ 2.40 GHz(cache 20 480 KB)，操作系统为Red Hat Linux 2.6.32-431.el6.x86_64，编译器为Intel FORTRAN Version 15.0.0.090。由于所求解的线性方程组均对称正定，因此全部采用PCG迭代进行求解。初始迭代向量选为全0向量，并在当前残向量的2范数与初始残向量的2范数之比小于1E-10时，迭代终止。在多重网格中，最粗层线性方程组的规模控制为100阶，且对该线性方程组，采用无填充的不完全LU分解预条件PCG进行求解，终止条件与外迭代相同。

实验针对6个稀疏线性方程组进行，包括Lin21、Lin22、Lin23、Lin31、Lin32与Lin32。所有线性方程组都采用有限差分离散得到，其中Lin21、Lin22与Lin23从离散二维偏微分方程的Dirichlet边值问题得到：

-a1∂2u/∂x2-a2∂2u/∂y2=f

(1)

定义域为(0,1)×(0,1)，函数f与边界条件从真解u=1得到。在每个维度上有n+2个点，其中n=1 024，且对任意连续函数u，将值u(xi,yj)定义为ui,j，其中xi与yj分别沿x与y方向上一致分布。线性方程组Lin21对应于a1=a2=1，且采用下述离散形式：

-ui,j-1-ui-1,j+4ui,j-ui+1,j-ui,j+1=h2fi,j

(2)

线性方程组Lin22对应于a1=1、a2=100，且采用下述离散形式:

-100ui,j-1-ui-1,j+202ui,j-ui+1,j-100ui,j+1=h2fi,j

(3)

线性方程组Lin23对应于a1=a2=1，且采用的离散形式为:

-ui-1,j-1-4ui,j-1-ui+1,j-1-4ui-1,j+20ui,j-4ui+1,j-

ui-1,j+1-4ui,j+1-ui+1,j+1=h2fi,j

(4)

线性方程组Lin31、Lin32与Lin33从离散三维偏微分方程的Dirichlet边值问题得到：

-a1∂2u/∂x2-a2∂2u/∂y2-a3∂2u/∂y2=f

(5)

定义域为(0,1)×(0,1)×(0,1)，函数f与边界条件从真解u=1得到。在每个维度上有n+2个点，其中n=128，且对任意连续函数u，将值u(xi,yj,zk)定义为ui,j,k，其中xi、yj与zk分别沿x、y与z方向上一致分布。线性方程组Lin31对应于a1=a2=a3=1，且采用下述离散形式：

-ui-1,j,k-ui,j-1,k-ui,j,k-1+6ui,j,k-ui+1,j,k-

ui,j+1,k-ui,j,k+1=h2fi,j,k

(6)

线性方程组Lin32对应于a1=1、a2=10与a3=100，且采用下述离散形式：

-ui-1,j,k-10ui,j-1,k-100ui,j,k-1+222ui,j,k-ui+1,j,k

-10ui,j+1,k-100ui,j,k+1=h2fi,j,k

(7)

线性方程组Lin33对应于a1=a2=a3=1，且采用的离散形式为：

27ui,j,k=h2fi,j,k

(8)

本文所有实验结果的时间单位均为秒，在所有表中，p的含义如第1节中所述，V、W分别表示采用V-与W-循环的多重网格，K25与K35分别表示采用参数t=0.25与t=0.35的K-循环网格。所有表中SQ表示正方分割，MI表示最小界面分割，ST表示逐步单向分割。

求解线性方程组Lin21所用的迭代时间如表1所示，在此测试用例中，系数矩阵每行中的非零元个数为5，且各向同性。从表1可以看到，当采用Jacobi光滑时，绝大部分情况下，ST优势明显。当采用Gauss-Seidel光滑时，MI更具有优势。

求解线性方程组Lin22的时间结果如表2所示，在此测试用例中，系数矩阵每行中的非零元个数依然为5，但该问题具有很强的各向异性。在表2中，“-”表示在1 000次迭代内未能达到迭代收敛条件。从表中可见，采用Jacobi光滑时，依然是绝大多数情况下，算法ST更具有优势。在采用Gauss-Seidel光滑时，对V-与W-循环，在p较小时，一般MI最优，当p取8时，SQ具有明显优势；对K-循环，一般ST更有优势。特别值得注意的是，在p较小时，对K-循环，SQ与MI都存在1 000次迭代内未达到收敛标准的情况，但ST不存在这个问题，这说明ST具有更好的健壮性。

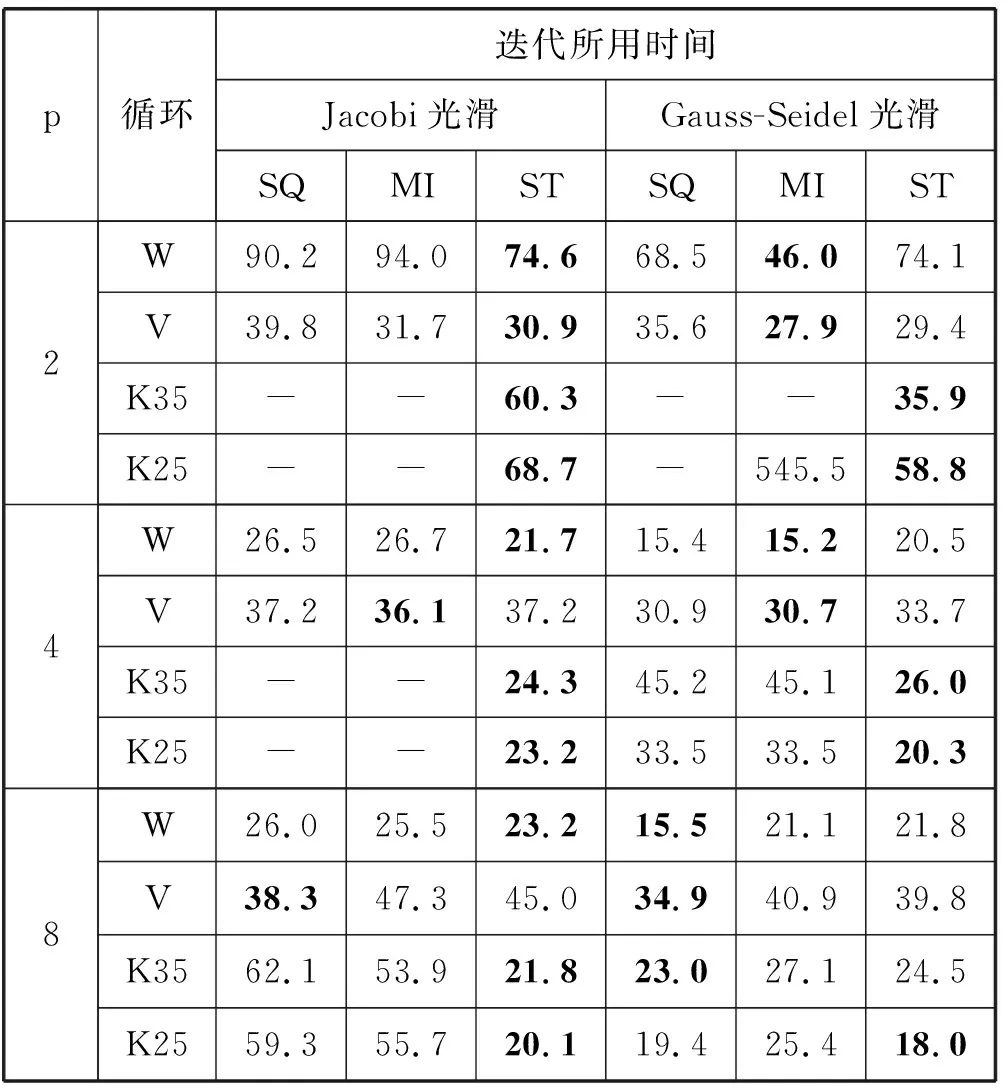
表2 求解线性方程组Lin22的时间 s

求解线性方程组Lin23的时间结果如表3所示，在此测试中，系数矩阵每行中的非零元个数为9，该问题具有一定的各向异性。对迭代阶段所用时间而言，对W-与V-循环，大部分情况下，MI更好。对K-循环而言，特别是在p较大时，ST更有优势。

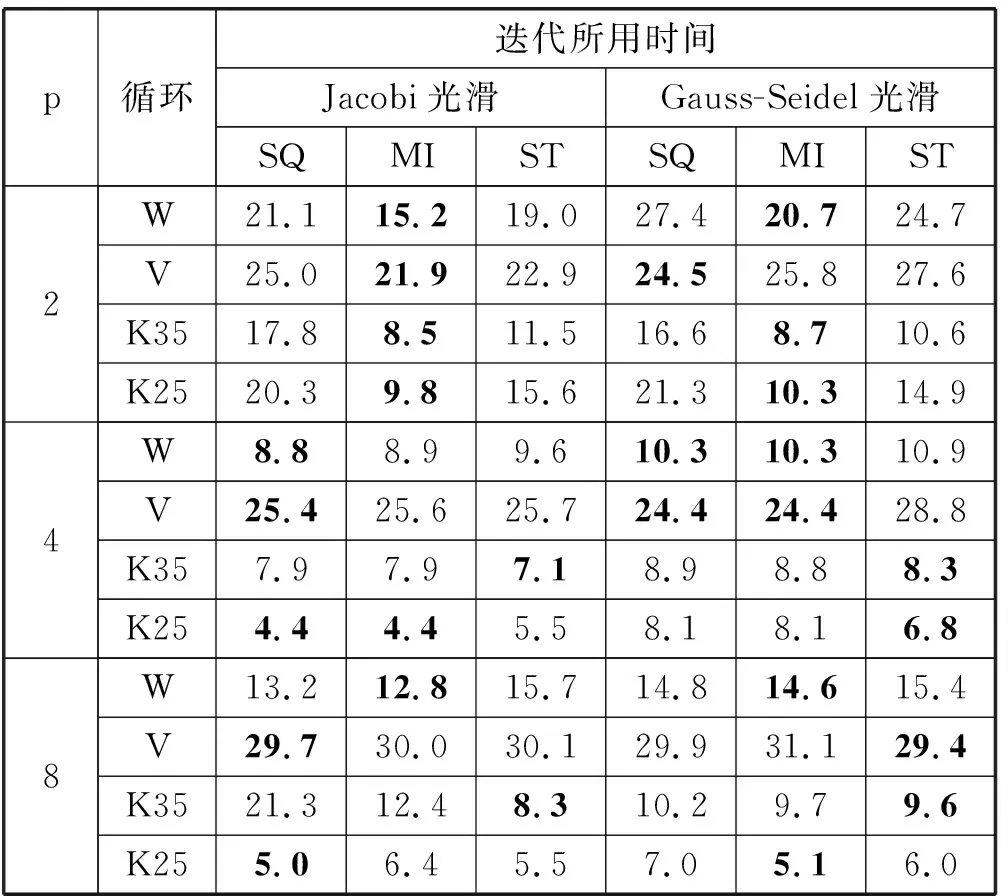
表3 求解线性方程组Lin23的时间 s

求解线性方程组Lin31、Lin32与Lin33的结果分别如表4、5与6所示。从表4可见，对系数矩阵每行中只有7个非零元的三维同构问题Lin31，当采用Jacobi光滑时，ST一致性地具有优势。当采用Gauss-Seidel光滑时，MI一致性地具有优势。

从表5可见，对每行中非零元个数较少的各向异性问题Lin32，采用Jacobi光滑时，一般ST具有优势。当采用Gauss-Seidel光滑时，对V-与W-循环，一般SQ更优，而对K循环，一般ST更优。从表6可见，对系数矩阵每行中具有很多非零元的各项同性问题Lin33，一般采用MI更有优势，采用SQ时，效果也相差不大。

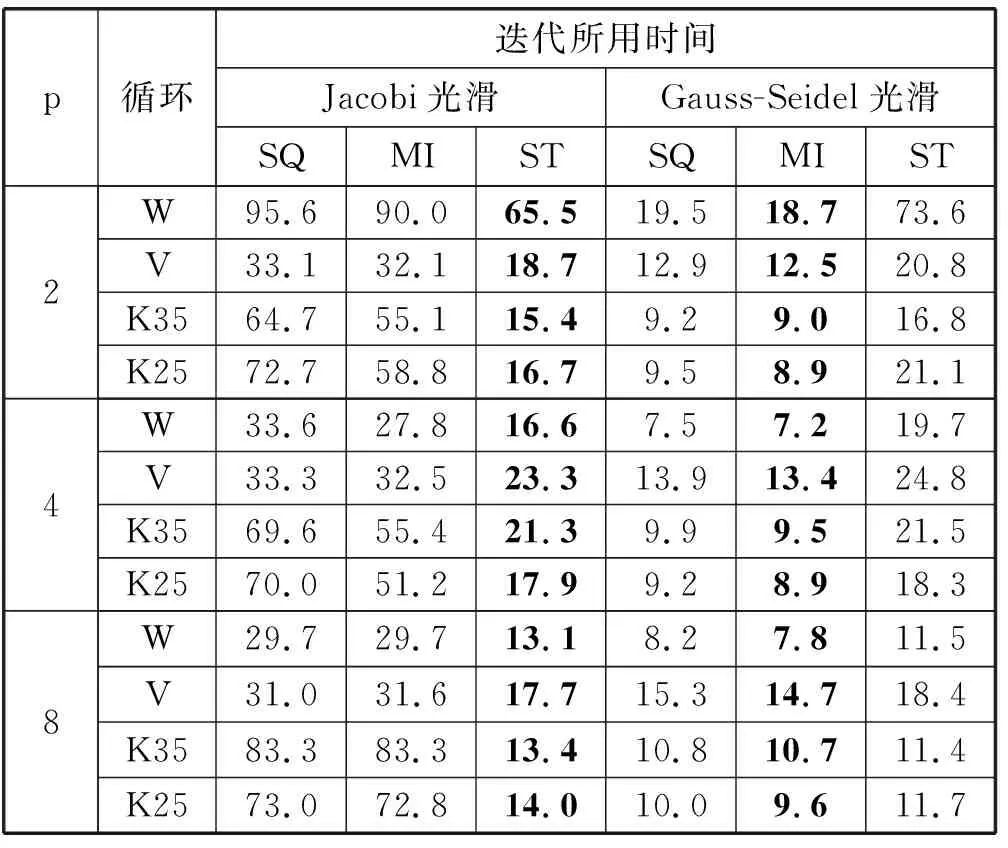
表4 求解线性方程组Lin31的时间 s

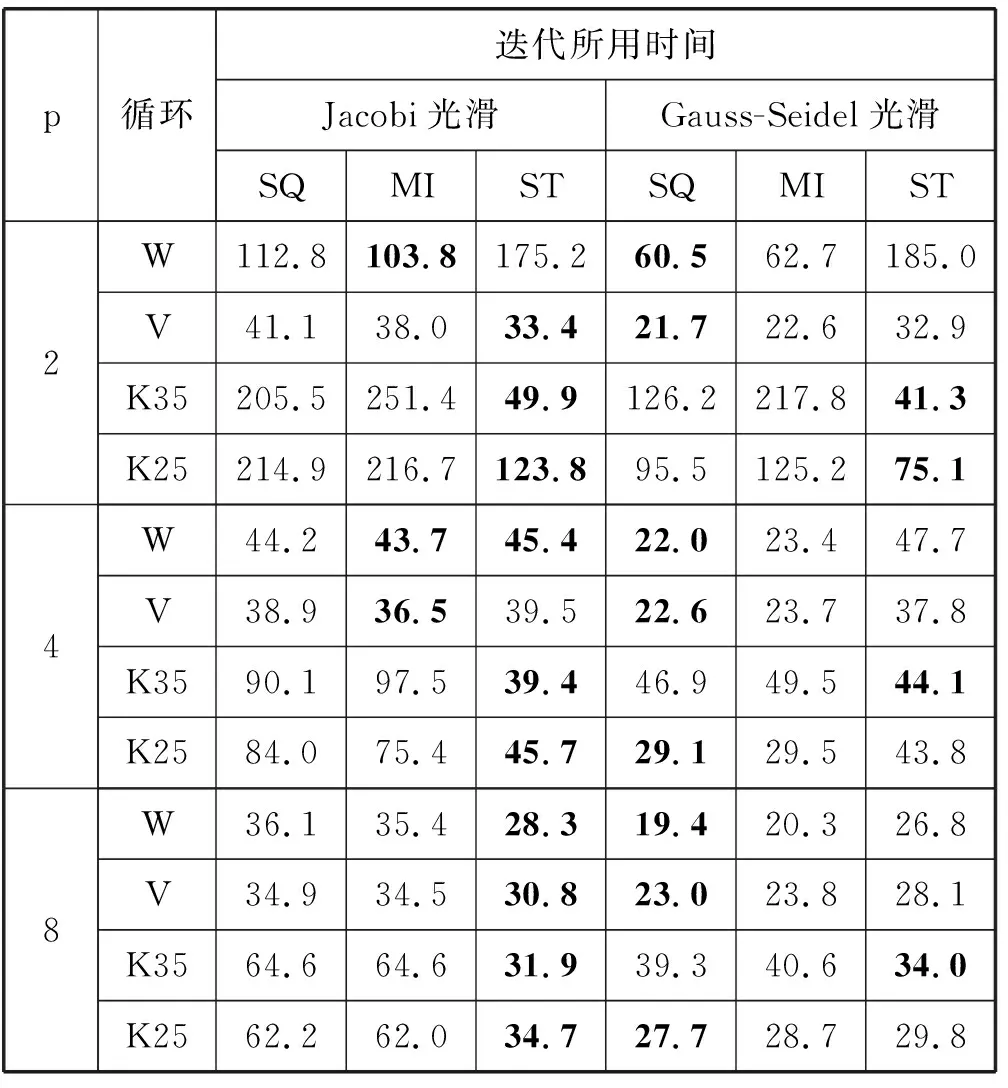
表5 求解线性方程组Lin32的时间 s

表6 求解线性方程组Lin33的时间 s

4 结 语

本文针对基于坐标分割的聚集型代数多重网格预条件，提出了正方分割、最小界面分割与逐步单向分割等三种坐标分割的算法，对其进行了高效实现，并通过从二维与三维模型偏微分方程离散所得同构与异构、每行中非零元个数较少与较多等多种类型的问题，对其进行了对比实验与分析研究。实验结果表明，当采用Jacobi光滑时，除了系数矩阵每行中非零元个数较多的情况之外，一般采用逐步单向分割更有优势。当采用Gauss-Seidel光滑时，一般采用最小界面分割算法更优。此外，当系数矩阵每行中的非零元个数较多时，一般采用最小界面分割算法更有优势。对K-循环多重网格，一般采用逐步单向分割算法也更具有优势，而且，这种分割的健壮性更好，即使对强各向异性的问题，最终所得多重网格预条件迭代的效果也相当稳健。需要说明的是，本文主要针对模型偏微分方程离散所得稀疏线性方程组进行了算法的测试与验证，虽然既针对各项同性与各项异性的问题进行了实验验证，又针对每行中非零元个数较少与较多的情况进行了测试分析，但对实际大规模科学与工程计算领域中的需要求解的稀疏线性方程组，一方面可能所得系数矩阵每行中的非零元个数更多，且每个坐标可能对应于多个自由度，如对混凝土细观数值模拟，采用六面体单元离散时，对应系数矩阵中每行含有约81个非零元素，且每个坐标通常对应于3个应变分量。同时，这里模型问题对应的系数矩阵都是M矩阵，而实际应用问题中对应的系数矩阵有时并不具有这种性质。虽然本文给出的算法对待求解的稀疏线性方程组并没有上述限制条件，但实际应用效果有待实验验证。因此，下一步将就本文给出的算法，对混凝土细观数值模拟等实际应用领域中的稀疏线性方程组，进行分析验证。