基于蚁群的无线传感器网络漏洞检测技术研究

凌 春 孙文胜

(杭州电子科技大学通信工程学院 浙江 杭州 310018)

0 引 言

在过去的几年，无线传感器作为一个热门话题被广泛应用于各种领域，例如边界检测、环境检测[1]和健康监控[2]等。大多数应用都需要网络的完全覆盖和持续连接，但传感器是随机投放并散列分布在网络中，这种随机部署[3]的传感器覆盖范围有限，容易出现漏洞。除此之外，网络节点是依赖电池供电且不可再生，能量消耗过快也会导致漏洞的出现。为了解决网络漏洞问题，就要设计一种在网络覆盖范围内能够快速地检测和定位漏洞的技术，这种设计可以通过识别漏洞边界处的节点来实现。

文献[4]提出了一种基于Voronoi图的覆盖漏洞边界检测算法，起始阶段建立无线传感器网络的Voronoi图，通过比较节点的监测范围以及当前节点到Voronoi图中顶点的长度来识别当前节点是否在网络漏洞边界上。文献[5]提出了一种基于几何计算的分布式算法，利用当前节点与相邻的两个邻居节点之间形成的几何三角和外接圆圆心的位置关系来判断当前节点是否在漏洞边界上，该算法计算复杂度较低，但限制了节点的监测范围和通信距离，适用范围较小。文献[6]提出了一种基于圆搜索的分布式覆盖漏洞检测算法，该算法根据圆周覆盖和邻居节点的信息建立了一张关系表，用于记录当前节点和邻居节点之间的距离和象限信息。通过查询关系表来定位网络漏洞所在的位置。该算法仅需要查询关系表即可获得漏洞信息，减少了节点之间的通信次数，但由于需要记录每个节点上的参数和圆弧信息，当节点个数较多时，执行时间较长效率低下。

为了解决现有的网络漏洞定位技术的局限性，提出了基于蚁群算法[7]的漏洞检测技术。蚁群的寻路特性能够有效解决传感器节点部署和路由优化的许多效率问题，能够及时准确地识别漏洞边界的节点。根据蚂蚁的动态特性，从两方面对传统方法进行了优化：一方面是采用分布式技术[8]，节点之间只需少量数据通信；另一方面是蚁群算法会自动调整蚂蚁的数量来检测不同大小的漏洞。

1 网络模型定义

为了对网络覆盖漏洞进行更好地检测和定位，首先介绍节点的初始条件和漏洞模型。

根据文献[9]的描述，假定将m个传感器节点随机部署在特定区域内进行监测，并且假定节点一旦放置就静止不动。每个节点都有最大的监测半径Rs和最大通信半径Rc，通常设置Rc=2Rs。邻居节点表示以当前节点为圆心，以Rc为半径区域内的传感器节点。

网络模型如图1所示，且具有如下规定：

(1) 漏洞的循环周期。由不重复的节点集合组{ni|i∈[1,m]}组成，其中ni+1是ni的邻居节点，nm是n1的邻居节点，且满足i≠j，ni≠nj。

(2) 最小周期循环。环内部不再包含任何循环。

(3) 覆盖漏洞。网络中的一片连续区域且不被任何节点的监测范围所覆盖，图1中的S1和S2即为网络覆盖漏洞。

(4) 漏洞弧段。节点S的监测范围边缘未被邻居节点Sk(Sk∈S(Rs))所覆盖的边缘弧段。如图1所示，节点n1的漏洞弧段为Arc(ab)和Arc(cd)(Arc表示弧段)。

(5) 标签特征。网络中的每个节点新增一个初始值为1的标签特征，标签特征的值永远比当前节点的漏洞弧段个数多1。即图1中，Arc(ab)和Arc(cd)是节点n1的两个漏洞弧段，对应标签特征L1=3。

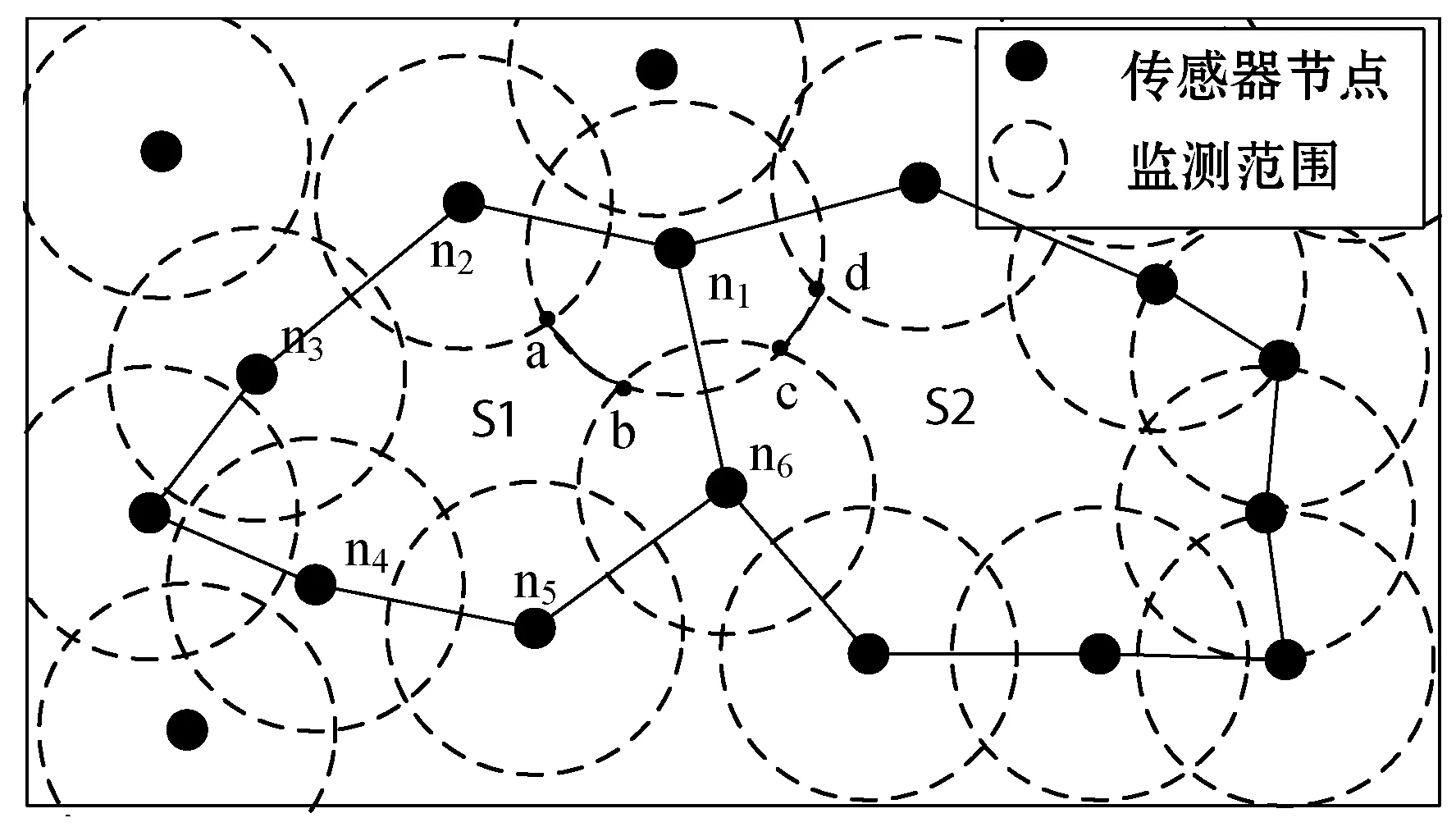
图1 覆盖漏洞和漏洞弧段图

为了检测覆盖漏洞所在的位置，应该先确认最小周期，并且最小周期必须是由节点的漏洞弧段组成。证明：假设最小循环周期至少包含一个非漏洞弧段Arc(ab)，这意味着节点n1在节点n6和n2之间还存在一个邻居节点n′。该现象将会产生两种情况：第一种，节点n6和n2其中一个或者两个都是n′的邻居节点，这意味着循环(n1,n2,…,n6)中存在另一个循环，这与规定(2)不符；第二种，节点n′仅是节点n1的邻居节点，那么节点n1在循环顺序中将出现两次，这与规定(1)不符，也不组成最小循环周期。根据上述的两种情况可知，漏洞弧段可用于识别拓扑中最小的周期，检测覆盖漏洞。

2 计算漏洞弧段

引用文献[10]中的几何计算漏洞弧段。假定节点ni是nj的邻居节点，ni和nj的坐标分别是(xi，yi)，(xj，yj)，ni到nj的直线距离是dij，则相对于节点ni节点nj的方向角αij如式(1)所示:

(1)

节点i被j覆盖的弧段所对应的方向角度如式(2)所示:

(2)

式(2)中θij对应的弧段点(xk,yk)和(xk+1,yk+1)如式(3)和式(4)所示：

(3)

(4)

节点i根据上述公式获取所有邻居节点的覆盖方向角的集合A={θij|j∈Vi}，集合A中的补集所对应的弧段即为寻找的漏洞弧段。

3 定位最小循环的蚁群算法

蚁群算法模拟蚂蚁在真实环境中的觅食特征[11]，以分布式的方式直接或间接地进行信息交互。改进的设计主要是利用漏洞弧段信息来引导蚂蚁的搜寻方向，从而定位出覆盖漏洞的位置。具体设计思路如下:

(1) 每个节点自动监测邻居节点的变化，确定漏洞弧段并计算对应的标签特征值。

(2) 蚂蚁由标签值L>1的节点启动以检测最小周期。

(3) 蚂蚁根据当前节点的标签、节点上的信息素浓度和邻居节点的距离来选择下一跳节点，并对访问过的节点释放信息素。

(4) 寻找到的最小周期通常是信息素浓度较高的节点形成的环。

根据上述设计的思路，覆盖漏洞的监测由传感器自行启动。当传感器节点的邻居信息变化时，每个节点根据漏洞弧段计算标签特征值L。当标签值L>1时，即该节点至少在一个漏洞的边界上，就启动一组蚂蚁，这些蚂蚁将从该节点出发进行巡视，直到返回该节点。

3.1 改进概率公式

蚁群算法搜寻过程是根据概率公式来选取下一跳节点，为了让蚁群算法适用于漏洞定位。将概率公式[12]加以改进，如式(5)所示。

(5)

式中：τij是边界(i,j)的信息素浓度，Lj是节点j标签值，dij表示当前结点i到j的直线距离长度，α、γ和β分别是信息素、标签值和两节点直线距离的加权因子。Vi是节点i中未被蚂蚁访问过的邻居节点的集合。

蚂蚁根据邻居节点的标签值会优先选取最小循环周期上的节点，这意味着标签值越大时，蚂蚁选取该节点的可能性就越大。此外，当一个节点存在多个互不相交的漏洞弧段时，则可知道该节点是多个不同方向循环周期的公共节点。由于单位时间内蚂蚁释放的信息素量固定不变，经过多次迭代，大多数蚂蚁都会选择最小循环周期上的节点，因此最小周期上的节点的信息素浓度相对较高。

3.2 改进加权因子

信息素加权因子只影响算法收敛速度并不会改变最终结果值，为了增加初始阶段算法的收敛速度，我们将α改进成式(6)所示。

α(t)=λ1(1+e-λ2t) 0≤t≤T

(6)

式中：参数λ1和λ2是常量，且λ1，λ2∈(0,1]，t表示搜寻时间，T表示最大搜寻时间。

式(6)表示在算法的初始阶段，加权因子α的值较高，节点信息素的增量较大，算法收敛速度较快；随着时间的推移，加权因子逐渐变小，算法的收敛速度也逐渐降低。

3.3 改进信息素和路径选择

为了避免蚂蚁在寻路过程中陷入局部最优解，改进信息素的更新策略使其更符合覆盖漏洞的定位。我们设置阈值限制信息素释放量，同时固定单位时间内信息素的增量，具体如式(7)所示。

(7)

式中：S代表阈值常量，Q是信息素增量，ρ是信息素挥发系数。因为蚂蚁大概率的选择具有较大标签值的节点，所以更容易寻找到最小周期的节点。

定位覆盖漏洞过程中，蚂蚁k自身维护一张列表Ak记录访问过的节点和对应的信息素量。等到所有蚂蚁执行完毕之后，寻找信息素总量最多的Ak所形成的环就是最小周期环。

3.4 蚁群算法检测漏洞的优势

该算法拥有许多优点：(1) 因为算法是分布式算法，不需要在节点之间共享信息，所以不会因为交换开销而过载。(2) 只要蚂蚁进入网络中，无论漏洞大小都会快速检测所有的漏洞。(3) 它比现有方法更灵活，因为在发现最小周期过程中，蚁群算法是根据邻居节点的信息素浓度、距离和标签值来选择下一跳节点。(4) 蚂蚁的最大数量和迭代次数是不固定的，这使得算法在应用时更具灵活性。但是，可以通过模型估算出应该启动的最大蚂蚁数量来提高执行效率，具体在下一节描述。

4 蚂蚁最大数量预估

不同的网络覆盖漏洞是由不同的最小循环周期构成，在相同的蚁群数量条件下，漏洞周长越长，蚁群算法定位所消耗的时间就越久。为了适应大小不同的漏洞，文献[13]提出了泊松分布来建立模型：

(8)

式中：λ>0，X是服从参数为λ的泊松分布，记作X～P(λ)。根据式(8)，假设漏洞出现在网络表面S中。其中S可以被分成n个不相交的扇区S(θi)，且满足i∈{1,2,…，n}，θ1+θ2+…+θn=360°。根据式(8)设计漏洞出现在扇区S(θi)上的概率：

(9)

对式(9)进行积分，求出在θi和θi+1之间的漏洞出现的概率：

(10)

根据式(10)，我们首先查询在扇区S(θi)中存在的节点个数mi，然后由式(11)和(12)分别得到预估扇形S(θi)区域内需要的蚂蚁数量Ni和蚂蚁的总数量N。

Ni=mi×P(xi)

(11)

N=N1+N2+…+Nn

(12)

若假设θi+1-θi≤θmax，那么根据式(11)和式(12)可以推测出蚂蚁最大数量不等式：

N≤∑P(xi)·mi·θmax

(13)

又因为P(Xi)≤1恒成立，则式(13)可以变成如下不等式：

N≤∑mi·θmax=θmax∑mi

(14)

若用M=∑mi表示网络S中所有节点的总个数，可推测出N≤M×θmax。因此为了快速定位网络表面S中的漏洞位置，可以启用最大数量的蚂蚁个数等于区域内的节点总个数与最大扇区角度的乘积。

5 实验分析

仿真环境采用MATLAB软件模拟评估所提出算法的性能。模拟参数如表1所示，将200个初始条件都相同的节点放置在100×200 m的网络范围内，每个节点的通信范围Rc=20 m。为了评估提出的算法,人为地在网络区域内部均匀分布覆盖漏洞，记录创建的漏洞的边界节点位置。设置信息素增量Q=2，权重因子β和γ为常量0.2，阈值S=88，挥发系数ρ=0.5、λ1=1、λ2=0.2。

表1 模拟参数设置

图2显示了迭代次数为10，不同蚂蚁数量和不同数量的覆盖漏洞检测效率百分比关系图。纵坐标表示定位到的漏洞边界节点数量占总漏洞边界节点数量的比例。这个比例实际上是用来判断漏洞检测效率高低。图2利用漏洞总个数分别为4、6、8和10的数量做比较，可以发现当网络中存在6个漏洞且蚂蚁的起始数量为20只的时候，效率却只有33.3%。但随着蚂蚁数量的增加，效率逐渐提高，直到蚂蚁数量达到55只时，效率达到了100%。事实上，当节点发送的蚂蚁数量越多时，网络节点被访问的数量就越多，这样就会发现更多的边界节点并标记信息素。此外，从图中可知，当蚂蚁数量相同时，漏洞数量越少，检测效率就越高。例如，只需要50只蚂蚁就可以在总漏洞数为4的网络中达到100%的效率。而对于漏洞总数为10的网络却需要近90只蚂蚁才可以达到100%的定位效率。上述现象可知，网络中的漏洞总数越多，则需要更多的蚂蚁来有效发现边界节点的数量。

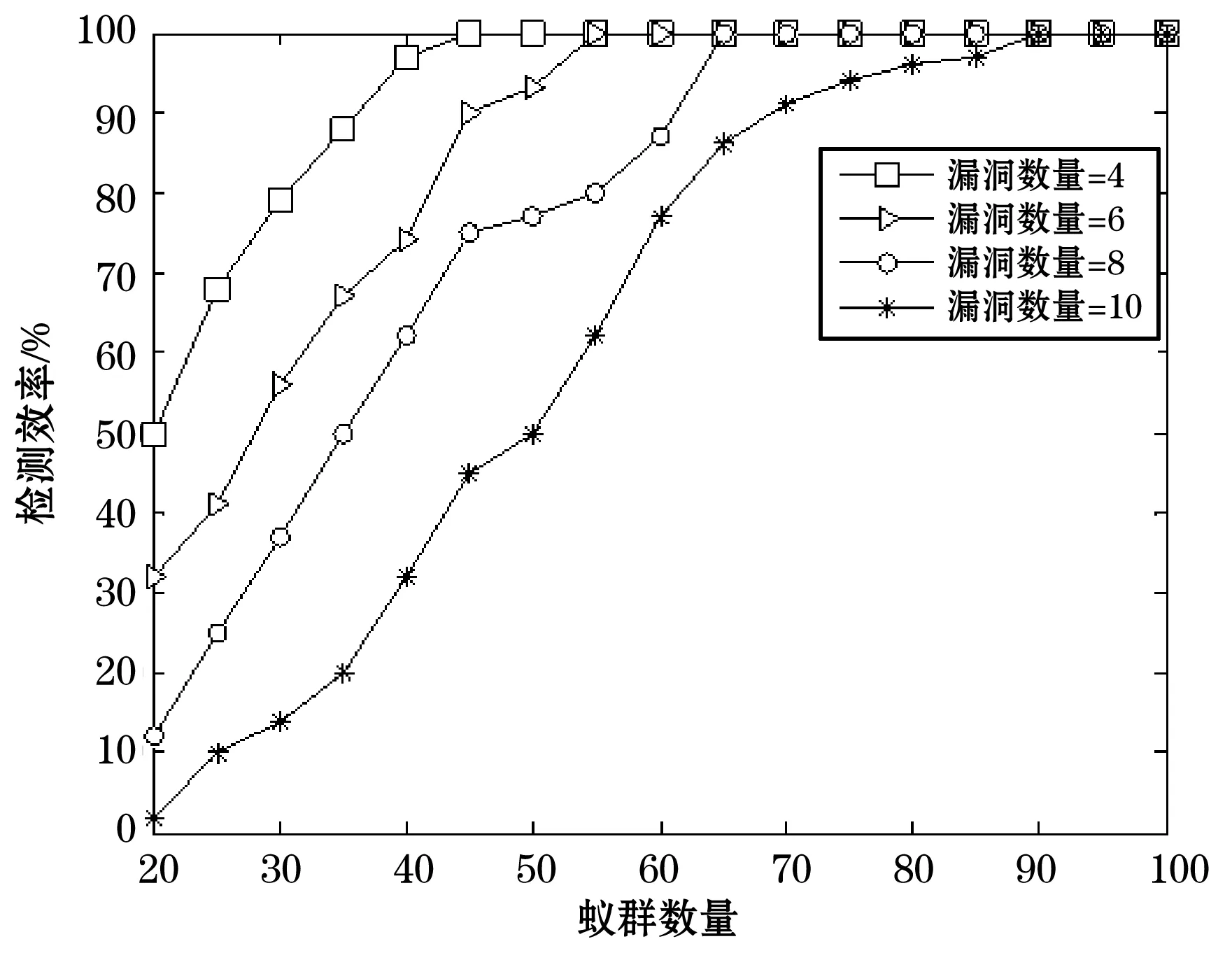
图2 蚂蚁数量和漏洞数量的效率比

图3表示在蚂蚁数量相同的情况下，不同漏洞数量的迭代次数和检测效率关系图。迭代指的是每个漏洞弧段节点重新启动一组蚂蚁执行所提出算法的次数。如图所示，随着迭代次数逐渐增加，漏洞边界上节点被检测数量也随之增加，检测效率也随之增加。但当蚂蚁数量一样时，网络范围内的漏洞数量越少，探测效率越高。这是因为当蚂蚁数量相同时，网络中的漏洞数量越多，则检测所有漏洞所需的时间就越长，所以效率也就越低。

图4表示在漏洞总个数为6和迭代次数为10的情况下，不同数量的蚂蚁和不同大小的漏洞与检测效率的关系。如图所示，检测效率随着蚂蚁数量的增加而增加，当边界节点个数为4时，只需要25只蚂蚁即可定位到所有漏洞，当漏洞边界节点个数为12时，需要60只蚂蚁才可以精确定位所有漏洞。由此可知，在相同的时间内，漏洞边界上的节点个数越多，则需要更多的蚂蚁来完成检测。

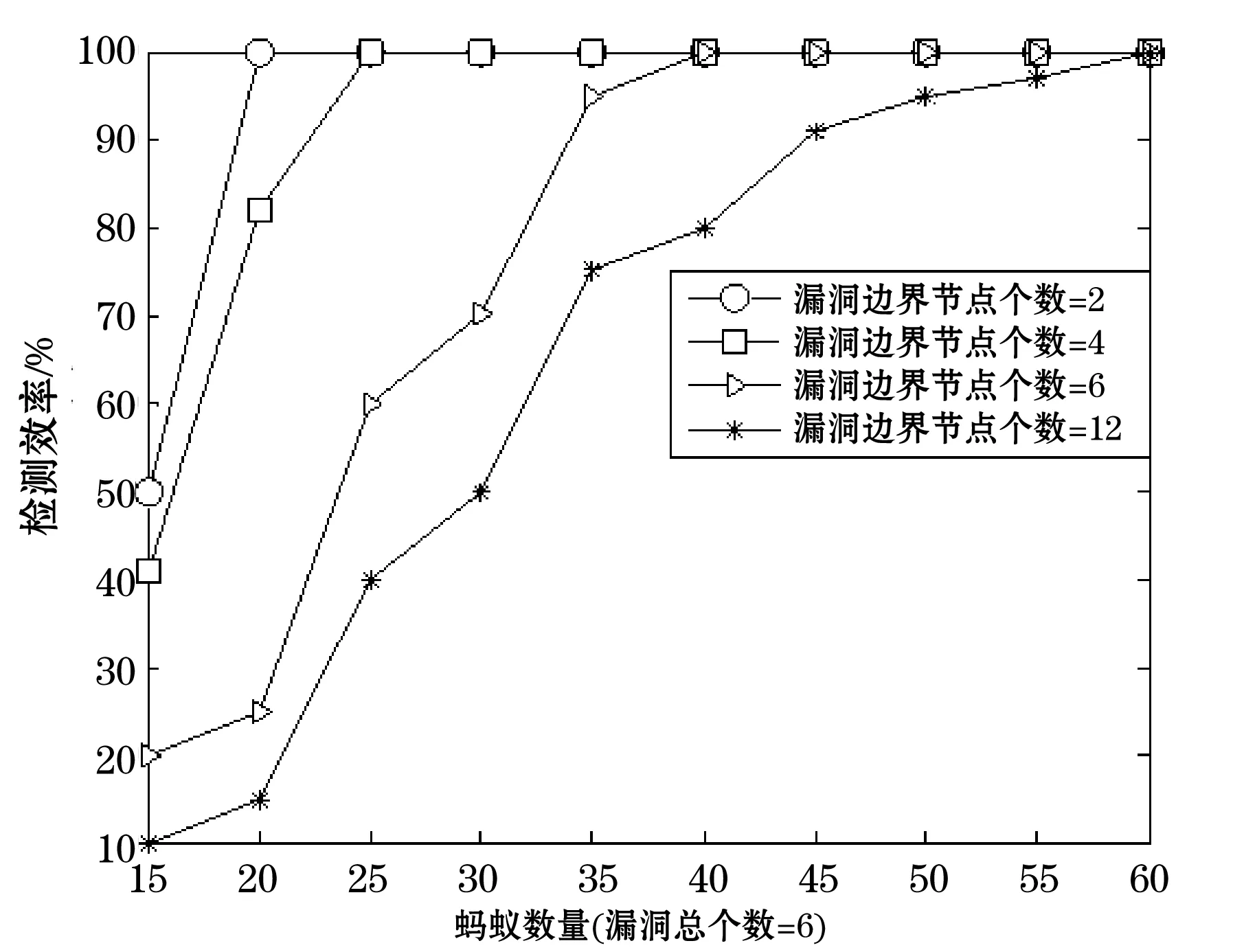
图4 蚂蚁数量和漏洞边界长度的效率比

6 结 语

本文采用通信方式，结合蚁群优化技术，针对无线传感器网络覆盖漏洞的问题做了一些研究：(1) 引入标签特征记录未被邻居节点覆盖的弧段数量；(2) 节点通过判断标签特征自发启动一组蚂蚁；(3) 利用蚂蚁的寻路特性获取漏洞边界的节点信息；(4) 利用泊松分布预估最大蚁群数量。实验结果证明：提出的算法能够以较低的复杂度高效精准地实现覆盖漏洞的定位。对于未来工作，可以利用本文设计的方法来开发解决无线传感器网络覆盖漏洞的问题。