架空输电线路地线滑车装置的构型设计与优化
2018-07-24谭永殿
谭永殿,马 俭,杨 鹏
(中国南方电网有限责任公司超高压输电公司百色局,广西 百色 533000)
0 前言
我国输电线路跨越了广阔的地域,在雷雨季节容易遭受雷击而引起送电中断,这是电力系统中发生停电事故的主要原因之一。布设架空地线是保护架空输电线路免遭雷闪袭击的重要措施,因此对架空地线的日常维护是一项非常重要的工作。
国内500 kV架空地线检修作业使用的滑车在现场适应能力欠佳,存在布设时间长、越障能力不足、综合移动性能差等诸多缺陷,同时也缺乏良好的安全防护措施。为响应现实需求,提出了一种形封闭锁合型、锥形导轮导向兼具刹车定位功能的地线滑车装置。
1 架空地线滑车装置的构型设计与分析
这种架空地线滑车装置的整机结构如图1所示,包括座板部件、锁合、越障导向和刹车机构(详见图2)。其中,座板部件用于承受高空作业人员的重量;形封板与横轴形成可拆卸的连接可使装置形锁合;两侧的越障导向轮则在地线上滑动导向,同时可越过防振锤等障碍;刹车机构用于定点作业时固定操作人员的位置。
越障导向与刹车制动是该装置的主要功能,越障导向轮的两端为圆锥体,通过中部的圆柱体连接。通常情况下,越障导向轮的圆柱部分在圆柱状的地线上滑动,两端的锥体则产生限位定心的作用,在越过大于圆柱部分宽度的障碍时越障导向轮圆锥部分便开始工作。刹车机构中驱动杆与槽型顶架之间采用螺纹连接,驱动杆上移时两侧的刹车臂便抱死架空地线,由此完成刹车功能。

图1 架空地线滑车的整机结构示意
2 地线滑车装置的主要性能分析
2.1 刹车机构运动学性能与相关性参数
刹车机构单侧刹车臂的运动如图3所示。该机构为驱动杆做平移运动的四杆机构,平移运动通过中间杆的平面运动后转化为刹车臂的定轴转动。

图3 刹车机构运动示意
由图3可以求得:

在ΔABC中运用余弦和正弦定理可得:

得出:

由此,在ΔAOC中可根据正弦定理求得lAO,lCO,O点为A点和C点的速度瞬心,可得:

再由υH/l4=υC/l3可求得刹车臂接触点的速度为:

对υH关于时间求导后可得:

2.2 刹车臂与接地线刹车接触力的计算
地线与刹车臂的前端存在正压力,在刹车臂与地线之间形成的接触力便是刹车力。带随机相位的双变量Weierstrass-Mandelbrot函数能仿真加权、随机重叠的隆起部状各向异性分形表面,该函数在直角坐标系下的表达式为:

式中:γ——分形粗糙面尺度因子;M——构造表面重叠隆起部的个数;n——频率指数;φm,n——在(0,2π)范围内均匀分布的随机相位;D——分形粗糙面分形维数;G——分形粗糙度;L——取样长度。
为简化计算,将本项目的圆柱状地线视为一个凸起,因此M=1,m=1,便可将式(9)变化为单自变量的函数:
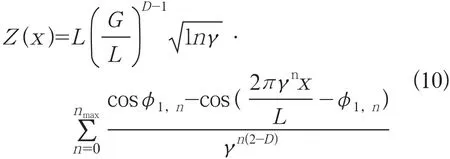
球体状凸体与刚性光滑平面的弹性接触如图4所示。
式中:r′——凸体微接触截面积的半径;r——凸体实际微接触面积的半径;E′——综合弹性模量; R——分形表面凸体顶端的曲率半径;δ——1个凸体顶端的变形量;pe——凸体所承受的法向弹性载荷。
1个凸体波形式的最长波长为2r,如果选择截止长度Ls=2r′,则此截止长度对应的频率指数的表达式为:

图4 地线与刹车臂的弹性接触

该函数的最大轮廓高度为:

对图4中的直角三角形利用勾股定理得:

由于δ远小于R,故:

将式(16)代入式(12)得:

1个微凸体实际微接触面积的半径为:

式中:E′——综合弹性模量。

由式(18)得:

1个凸体承受的法向弹性载荷也可写为:

根据式(20)和式(21)可得:

将式(16)代入式(22)得:

将式(23)代入式(20)中可得:

将式(17)代入上式中可得接触面的压力载荷为:

式(26)表明接触面的压力载荷与分形粗糙面尺度因子、分形粗糙度和综合弹性模量呈正相关关系,分形维数的增加不利于提高接触面的压力载荷。
2.3 越障导轮的越障能力分析
地线上安装的障碍物截面形状主要分为圆形截面(如防振锤)和方形截面,这2种截面与越障导轮的相对位置关系如图5所示。
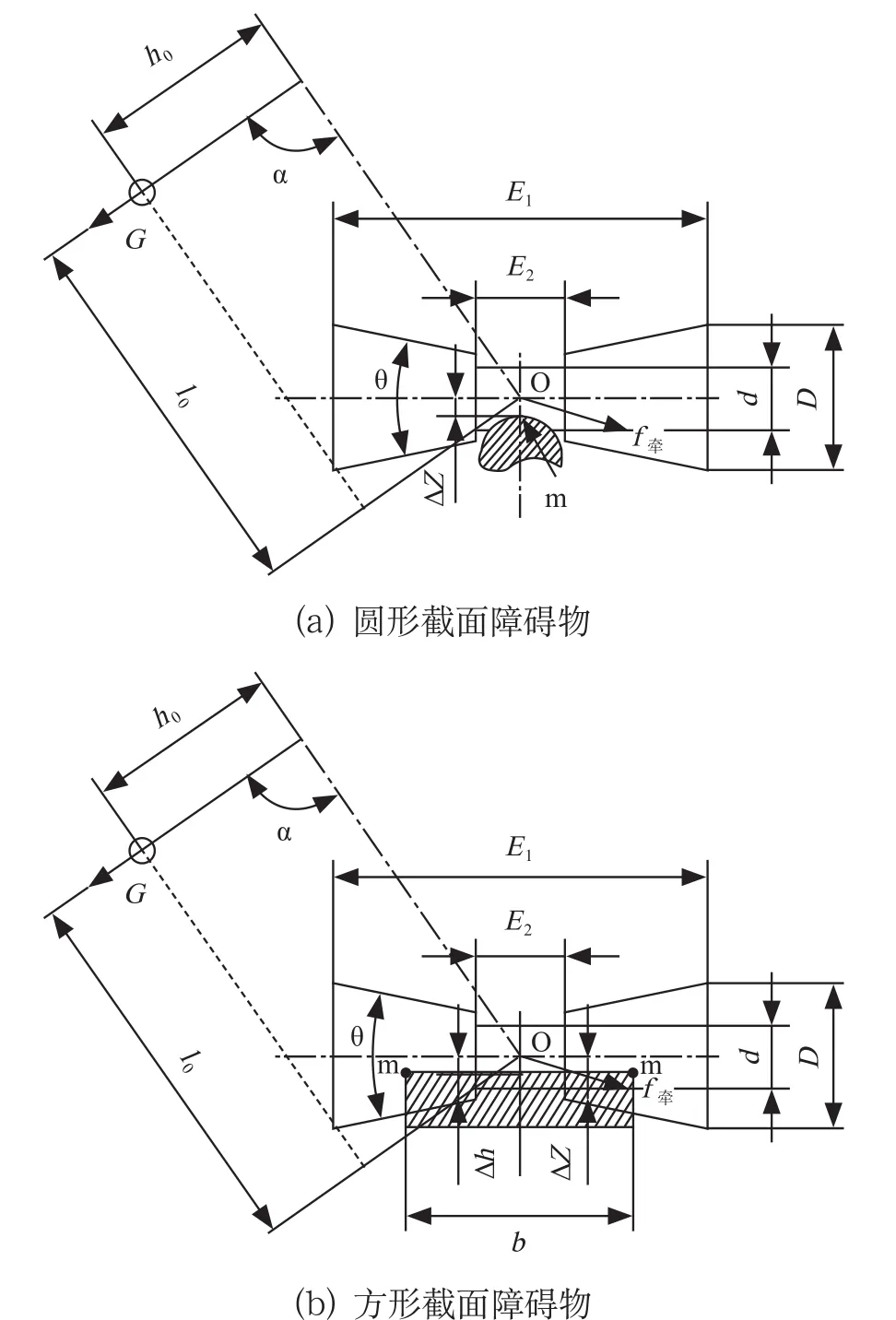
图5 障碍物与越障导轮的相对位置
其中:G——滑车及操作人员的重力;m——障碍物上的支点;f牵——水平越障牵引力,沿滑车前进方向与越障导轮垂直;Δz——牵引力的力臂;α——地线与重力方向的夹角。
滑车顺利越过障碍物需要满足:

对于图5中2种情况下滑车的越障原理相同,均分为如下2种情况:
① 当Δz≤d/2时,

则只要满足式(29),滑车便可顺利通过障碍物。

② 当Δz>d/2时,f牵的力矩方向与G相同:

综上所述,越障导轮中部柱体直径d与障碍物高度Δz间的关系是影响滑车越障能力的主要因素,只有满足Δz≤d/2时,滑车才能顺利通过障碍物。
3 地线滑车刹车机构运动仿真
3.1 建立虚拟样机
该项目包含的刹车机构是确保操作人员定点和安全作业的主要保证,各项性能指标均受结构的功能尺寸、材料、接触状况等的影响。结合现代仿真手段有助于快速深入地分析指标与影响因素之间的定量关系。由于刹车机构具有完全的空间对称性,且Adams本身自带的几何建模模块不够精准和逼真,所以根据机构运动简图建模时只能反映与运动特性有关的结构尺寸,仿真模型如图6所示。滑车刹车机构的约束类型如表1所示。

图6 刹车机构的实际结构与仿真模型

表1 滑车刹车机构的约束类型
3.2 仿真分析
调用ADAMS/Solver进行仿真分析获得各构件的运动特性。设置仿真时间end time为12,步数为500,驱动杆的移动函数为15sin(0.542×time),然后进行仿真。在仿真计算结束后,进入PostProcessor进行后处理。
3.2.1 刹车臂的运动性态与相关因素
刹车臂的运动性态主要体现为开合效率、闭合时对滑车稳定性的影响,其与主要因素之间的关系如图7,8所示。

图7 不同因素水平下刹车臂与地线接触点角加速度对比

图8 不同因素水平下刹车臂与地线接触点角速度对比
在图6中,brake_x和brake_y反映了刹车臂与驱动杆之间的距离,motion_x则体现了驱动杆的横向杆长,distance则显示了中间杆与刹车臂之间的铰接位置,图中计算了5个点位的目标值。由图7可知,brake_x和brake_y分别为152 mm和32.5 mm时刹车臂与地线接触点的角加速度值最低,目标值呈现下降趋势,distance和motion_x对目标值的影响规律相似,分别为60 mm和56 mm时目标值最低。从图7中可得出,增加刹车臂固铰点与驱动杆的之间的距离有助于提高刹车臂的平稳性。在4个因素中,中间杆与刹车臂的铰接位置对目标值的影响较为敏感。
图8中3条曲线呈现下降趋势,1条曲线呈现上升趋势。为提高刹车臂的开合效率,应减小brake_x,brake_y和distance,同时增加motion_x的值。
3.2.2 刹车臂接触力与相关因素关系及优化
刹车臂的接触力体现了滑车制动能力的大小,是关键功能参数之一。在驱动杆上施加35 N的向上牵引力,刹车臂与地线之间添加接触副,运行后得brake_x,brake_y,distance以及motion_x对刹车接触力的影响,如图9所示。

图9 接触力与不同因素水平的关系
以刹车接触力contact_Force最大为目标,设:
x1=brake_x,x2=brake_y,
x3=distance,x4=motion_x。
则优化模型为:

在图9的敏感性分析曲线中找到单因素下的各变量最佳值:
x0=[143 32.5 75 56]
以其为优化的设计变量初始值对仿真变量进行更改,随后进行优化,迭代曲线图10所示。
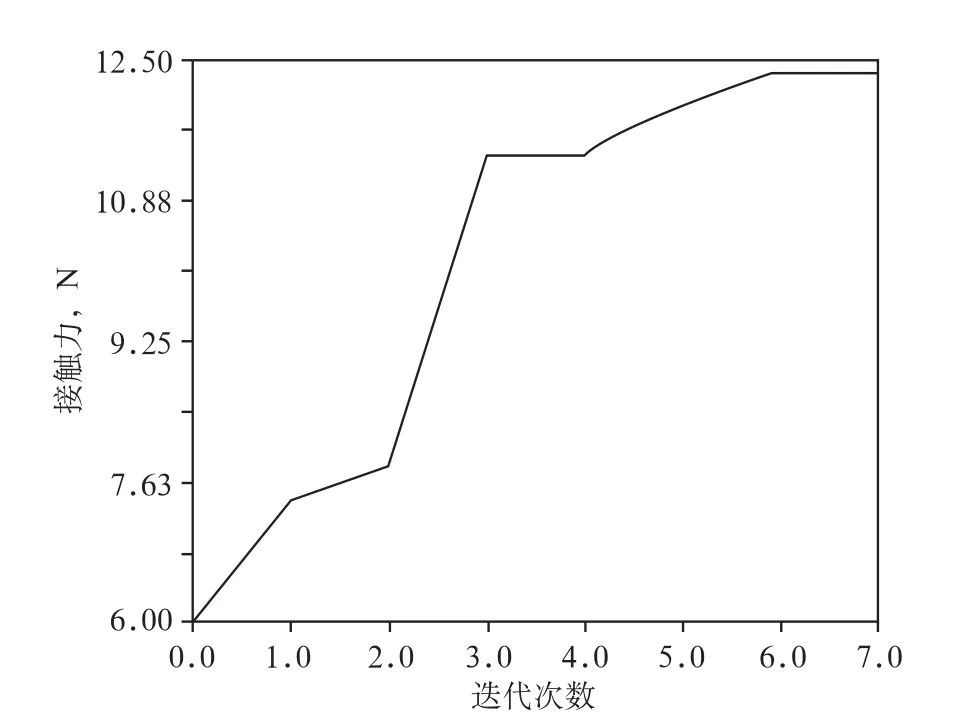
图10 刹车机构接触力迭代曲线
经过7次迭代后计算收敛,此时接触力达到12.36 N,较初始值提升2.06倍,优化效果明显。以驱动杆水平段长度为基准长度,可算得各杆的最佳长度比,即驱动杆∶中间杆∶distance=1∶1.86∶1.27。
4 结论
(1) 通过对装置的构型特征进行分析,表明本项目的机构具有形封闭的锁合能力,结构稳定性强,建立在制动能力上的定点作业适应性好。
(2) 通过计算可知,刹车机构的开合效率和平稳性与刹车臂长成正比,与摆角影响长度l3成反比,并且与中间杆、刹车臂安装位置和驱动杆长均有密切关系。
(3) 接触力的计算结果表明,分形粗糙面尺度因子、分形粗糙度和综合弹性模量均能正向影响接触面间压力载荷;改变接触面材料性质是增加接触力较直接的手段。
(4) 滑车越障能力分析表明,要使滑车顺利越过障碍物,需要障碍物的顶端低于越障导轮的滚动中心。
(5) 仿真分析表明,中间杆与刹车臂的铰接位置对刹车臂的速度、加速度影响最为显著。按如下配置刹车机构各杆的最佳长度比,即驱动杆∶中间杆∶distance=1∶1.86∶1.27有利于提高刹车臂与地线之间的接触力。
