一类超线性Schrödinger方程非平凡解的存在性

，，

随着科学技术的不断发展，非线性泛函分析能很好地解释自然界各种现象，已成为现代数学的重要研究方向.非线性Schrödinger方程来源于数学物理、数学生物和物理学等学科，目前研究[1,2]较为活跃.

本文研究下面超线性Schrödinger方程解的存在性

(1)

h(x,t):RN×R→R+是一个连续函数,并且满足

(h1) 当t≤0,h(x,t)=0;当t→0+,在RN中一致有h(x,t)=o(|t|);

(h4)在RN中,μ>2对∀t≥0有0≤μH(x,t)≤th(x,t)；

1 证明

显然 (1)的解是下面泛函的临界点

(2)

由于泛函I(u)在一般的Sobolev空间H1(RN)没有定义,所以我们进行如下变量变换

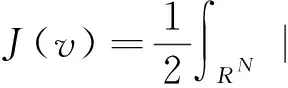
(3)

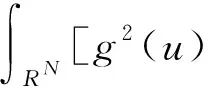
(4)

(5)

(6)

1.1 引理 1.1[3]

证明见文献[4].接下来，建立山路引理的几何条件[3].

1.2 引理 1.2 存在ρ0,a0>0,使得所有的‖v‖=ρ0,均有J(v)≥a0.

证明：令

则由(h1)(h2)和引理1.1得

(7)

(8)

因此存在常数C>0,使得

(9)

有

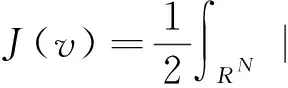
(10)

所以当‖v‖=ρ0时,选择很小的ρ0,结论成立.

1.3 引理1.3 存在v∈H1(RN),使得J(v)<0.

事实上,因为G-1(v)≤v,由(h4)和引理2.1,当t→+∞时,我们有

(11)

结论得证.

由引理1.2和1.3的结果，根据山路引理，对于常数

其中Γ={γ∈C([0,1],H1(RN)),γ(0)=0,γ(1)<0},存在一个关于c的Cerami序列{vn},即J(vn)→‖vn‖)‖J′(vn)‖→0.

有如下引理：

1.4 引理1.4

对于任意的c>0,J的任意Cerami序列有界.

证明设{vn}⊂H1(RN)是一个Cerami序列.用反证法，假设{vn}无界，且满足

J(vn)→c,‖vn‖→+∞,‖J′(vn)‖→0.

(12)

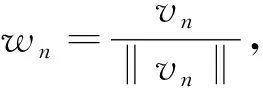
我们声明

(13)

否则,对于一些常数δ>0,我们有

(14)

因此,根据(h3)和引理1.1,我们可得

(15)

利用引理1.1和(15)，我们有

(16)

显然矛盾!所以(13)得到证明.

1.5 Lions集中紧引理

根据Lions集中紧引理,在空间Lr(RN)中,我们有wn→0,g∈(2,2*).

现在，我们定义一族线性泛函TnH1(RN)→R,如下

有

(17)

所以,{Tn}是一族定义在H1(RN)上的有界线性泛函.从共鸣定理知,{Tn}对n一致有界,即:存在与n无关的常数C>0,使得‖Tn‖(H1(RN))*

在(2.17)选择φ=wn，在空间Lr(RN)上有wn→0r∈(2,2*),可以得知

(18)

显然矛盾！因此原假设不成立，{vn}有界，引理1.4得证.

2 主要结论

(19)

因为{vn}是一个Cerami序列,根据引理1.4知{vn}有界，所以存在v∈H1(RN),使得H1(RN)vn→v.由Lebesgue 控制理论,得

(20)

所以，v是(1.1)的一个弱解.

下面证明v≡0,反证法：假设v=0,则对所有的R>0,有

(21)

即{vn}消失,通过Lions集中紧引理,对任意的r∈(2,2*),在Lr(RN)中vn→0,因为t=G(G-1(t))≤g(G-1(t))G-1(t),由引理1.1和(h1)-(h2),我们有

(22)

这意味着

(23)

由δ→0和q∈(2,2*)得

(24)

由

(25)

所以

(26)

由引理1.1,(24)和(26),当n→∞时,我们有

这样得到了一个矛盾结果J(vn)→c>0.所以,存在V(x),R>0和{yn}⊂RN,使得

(27)

所以推得