人字齿轮工艺空刀槽的设计方法

徐 瀚

（中国中车戚墅堰机车车辆工艺研究所有限公司，江苏 常州 213000）

人字齿空刀槽宽度的取值受到齿轮自身参数、滚刀参数、机床规格等众多因素的限制。如何在给定的外部条件下确定最优空刀槽宽度以及可行性，就成了设计人员和工艺人员关注的问题。本研究从滚齿空间数学模型出发，建立了最小空刀槽与外部影响因素的精确数学方程，结合滚齿工艺确定最优空刀槽宽度。

1 数学模型建立及方程求解

1.1 几何模型的建立设计

如图1所示，滚刀节线与被切齿轮节圆圆柱的切点p正好移动到空刀槽端面，此时滚刀并未完成这一端全部齿的切制，滚刀还需沿被切齿轮轴线继续移动超越量e才能完成该端齿的切制。建立坐标系o－xyz，o点该端空刀槽端面的轴心，z轴与被切齿轮轴线重合，x轴为o点与p点的连线，各轴方向如图1所示。坐标系o'－x'y'z'，o'点与p点重合，z'轴与滚刀轴线重合，轴与o点和p点的连线重合，各轴方向如图1所示。

图1 滚齿加工模型中各轴方向

设计工艺空刀槽的目的是为了在滚刀切制完成一端齿形后，退刀时不会与被切齿轮发生干涉，其干涉问题的几何模型就是轴线不平行的两圆柱体的相交问题，如图2所示，只要滚刀在完全退刀位置时，使空刀槽的端面不处于此时滚刀与被切齿轮产生的最大理论干涉区域中（滚刀足够长，与被切齿轮的干涉区域达到最大，图中空间相贯线内部阴影部分所示），则滚刀可以顺利完成退刀。从几何模型还可以得知，空刀槽下端面不与滚刀发生干涉的极限位置应该是下端面与相关线相切时，由此，若能准确求解出最大理论干涉区域即空间相贯线方程，就可为设计合理精确的空刀槽宽度提供理论依据。

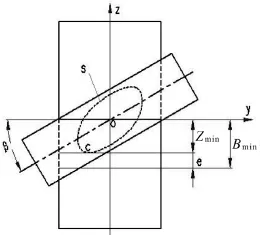
图2 滚刀与工件模型干涉区域的轮廓相贯线

1.2 滚齿退刀最小超越量e的计算

如图1所示，滚齿加工中，滚刀退刀时需要有一定超越量e，超越量是为使得滚刀与被切齿轮不再发生啮合即保证完全切削，超越量的最小值与齿轮参数和滚刀参数密切相关。现以左旋滚刀切削左旋齿轮为例分析退刀最小超越量。如图3所示，在滚刀法平面建立坐标系o－xy，根据斜齿轮的滚齿原理可知，被切齿轮与滚刀在法平面内相当于无侧隙啮合的齿轮和齿条，被切齿轮在法平面内为一椭圆，其平面方程为：

式中：rr为被切齿轮齿顶圆半径，β为被切齿轮分度圆螺旋角。

图3 滚齿加工时滚刀的位置模型

m'n'、mn为法平面滚齿啮合线，m'n'直线方程为：

式中：r为齿轮节圆半径、α为法面啮合角等于滚刀法面压力角αn。

滚刀顶线方程为：

式中：rr为齿轮顶圆半径、h为全齿高。

联立式（1）、（2）可以求得m'的x坐标为：

联立式（2）、（3）可以求得n'的x坐标为：

xn'=(r+h－rr)tanα

滚刀在法平面内的参与切削的长度一半为：

ln=max[｜xm'｜,xn']

由此可知，只要滚刀参与切削部分退到空刀槽上端面之下时，退刀完成可以保证完全切削，故最小超越量为：

emin=lnsinλ

式中：λ为滚刀安装角，λ=β±γ，γ为滚刀螺旋升角，“+”表示滚刀与齿轮旋向相反；“-”表示滚刀与齿轮同旋向相同。

1.3 最大干涉状态下最小空刀槽宽度的求解

如图1（a）坐标系所示，在o'－x'y'z'坐标系中滚刀顶圆圆柱方程为：

式中：rg为滚刀顶圆半径。

o－xyz坐标系中，被切齿轮齿顶圆柱方程为：

式中：rr为被切齿轮齿顶圆半径。

通过坐标变换可以求得滚刀顶圆圆柱方程在o－xyz坐标系中形式，o'－x'y'z'坐标系变换到o'－x'y'z'坐标系的转换式为：

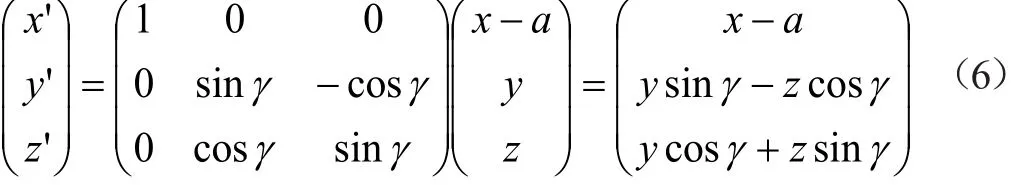
式中：a为滚切中心距a=rr+rg－h，h为全齿高，γ为滚刀安装角γ=β±λ，β为齿轮螺旋角，λ为滚刀螺旋升角。

通过（6）式代入（4）式中，可得滚刀顶圆圆柱在o-xyz坐标系中为：

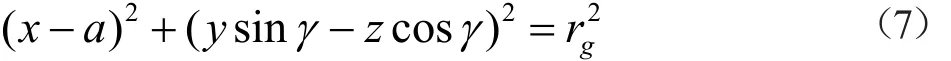
联立（2）、（4）可得滚刀顶圆柱与被切齿轮顶圆柱的相贯线方程为：

为简化求解，如图2所示，将模型向yoz平面投影，投影线与x轴平行，此时空刀槽端面不干涉的极限位置就是端平面在yoz平面上的投影直线与相贯线的投影曲线S相切时的位置，另外由于滚刀退刀时还有一段超越量e，所以理论可行的最小空刀槽宽度为切点c距y轴的距离加上超越量e，由图2分析可知，切点c也是相贯线的投影曲线z=f(y)的最小值Zmin所在点，由此可知最小空刀槽宽度为：

由（8）式可以写出相贯线在yoz平面的投影曲线S的方程为：

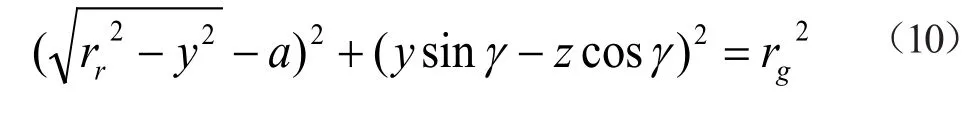
由图2（b）中坐标系可知：y'=ysinγ－zcosγ＞0，简化式（10）如下：

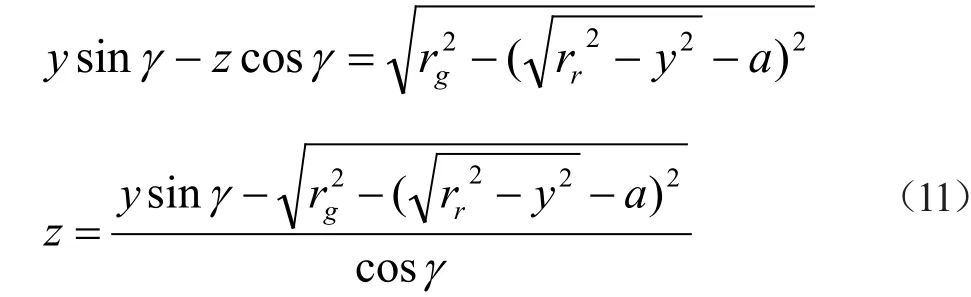
式（11）即为曲线S在第三象限的方程，z=f(y)取最小值应满足条件：f'(y)=0，式（11）对y求导得：

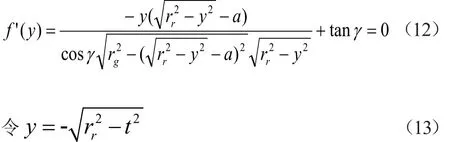
将式（13）代入式（12）中可得：

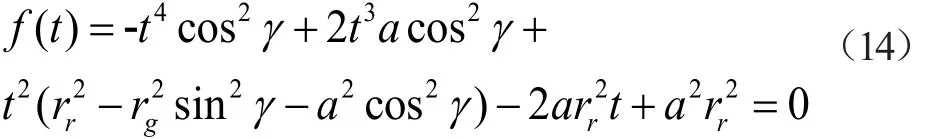
式（14）为关于t的一元非线性方程，可以使用MATLAB 7.0直接解出t，计算结果代入式（13）解出c点横坐标值cy，将cy值代入式（11）可以解出cz，再联合式（9）便可以求出Bmin。

1.4 非最大实际干涉条状态下最小空刀槽宽度的求解

存在另外一种情形，即滚刀长度有限使得实际干涉区域y方向的最小值小于最大干涉区域y方向最小值，滚刀与被切齿轮实际干涉区域如图4阴影部分所示。

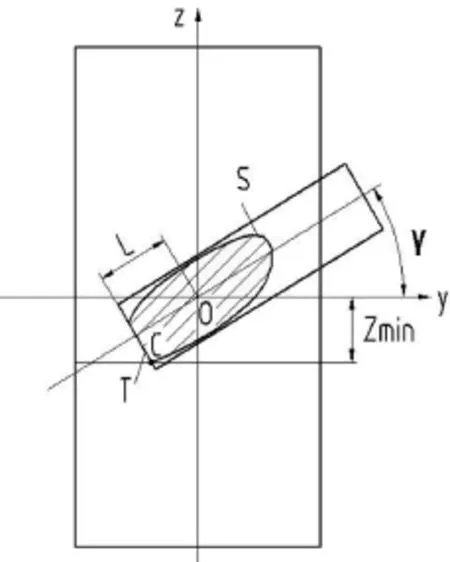
图4 滚刀与被切齿轮实际干涉区域

建立同图（1）坐标系，分析可知，此时Zmin等于滚刀端面投影直线T与相贯线投影曲线S的交点c'的纵坐标值c'z，滚刀端面投影T的方程为：

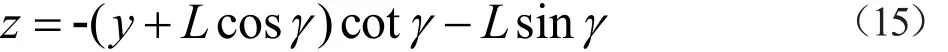
式中：L为滚刀端面距节点的轴向距离。

联立式（10）、（15），可求的交点c'的坐标，化简后为：

式（16）为z的一元非线性方程，通过MATLAB 7.0易解得c'（z舍去一个z值较大的点），将cz=c'z值代入式（9）便可求的Bmin。

1.5 滚齿干涉情形判别

设计滚齿空刀槽时，首先要根据滚刀、被切齿轮及其安装参数判断干涉类别，然后根据相应的计算公式进行计算，分析可知，临界条件为滚刀端面投影直线T'经过相贯线投影曲线S的z轴最低点c，此时临界直线方程T'满足下式：

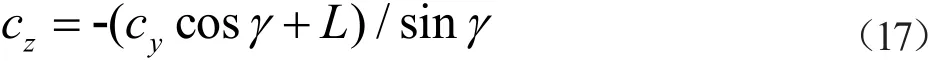
式中：cz、cy为1.1.3中计算出的c点坐标值。

故若 cz＞ -(cycosγ +L)/sin γ，表明实际滚刀端面投影直线T在临界位置下方，最小空刀槽按1.3情形计算；反之按1.4情形计算。

2 结语

（1）本研究根据滚齿的几何模型，提出了针对干涉区域的数值计算方法，并以此推导出了人字齿最小空刀槽的精确计算公式。

（2）研究理论是建立在精确数学模型基础上，尤其是对人字齿滚齿及磨齿的最小空刀槽宽度的计算精度极高，因此，文中理论及公式可直接应用于实际生产中人字齿空刀槽的设计。