基于能量回归滤波全变分图像自适应去噪算法

羊梅君

(华南理工大学广州学院 电子信息工程学院，广东 广州 510800)

0 引 言

图像作为取得信息的主要方法之一，信息的准确获取受图像质量的影响[1]。但是，在取得图像和传输图像的过程中因为设备、环境等外部因素的作用，图像内大多含有噪声[2]。噪声的存在会影响图像中有效信息的提取，所以分析图像前对图像进行去噪具处理具有十分重要的作用，因此，在图像处理领域内，图像去噪一直是一个研究比较多的热点课题。传统的基于图像局部方向特性的自适应全变分去噪算法[3]，存在速度慢、稳定性差的缺点，为了解决这些问题，本文提出了一种基于能量回归滤波全变分图像自适应去噪算法，结合了能量回归滤波能够保存图像边缘的特点，基于参数P与λ的全变分图像自适应去噪算法保存图像细节的优势，实现图像快速、稳定的去噪。

1 基于能量回归滤波全变分图像自适应去噪算法

1.1 采用能量回归尺度空间滤波法获取滤波图像

1.1.1 空间尺度滤波

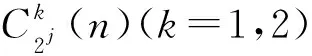
(1)

(2)

(3)

(4)

1.1.2 回归因子的选择

(5)

那么：

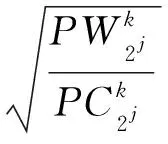
(6)

通过这种方法对源图像f(n)=f(n1,n2)实施尺度空间滤波计算时，尺度空间滤波算法就可以称为能量回归滤波算法[8]。

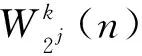
对能量回归滤波算法的具体过程进行总结：

对二维离散图像f(n1,n2)(1≤n1,n2≤N)及分解层数J(1≤J≤Iog2N)实施设置；

在不同尺度上对式(7)、(8)、(9)、实施运算；

C2j(n1,n2)=W2j(n1,n2)·*W2j+1(n1,n2)

(7)

(8)

(9)

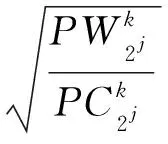
(10)

(11)

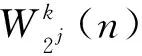
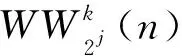
(12)

1.2 基于参数P与λ的全变分图像自适应去噪算法实现图像去噪

在使用能量回归滤波法获取到的滤波图像上实施基于参数P与λ的全变分图像自适应去噪算法，实现图像最终去噪。

首先，对滤波图像局部功率进行设置[9]：

(13)

1≤p≤2

(14)

与式(14)相应的欧拉-拉格朗日方程描述为：

(15)

(16)

将式(15)等号两侧都乘以u-u0-C后，于全部图像Ω局部内积分，能够得到：

(17)

式(17)内，Q(x,y)=(u-u0-C)通过式(17)实现的充分必要条件能够获取规整化可信度参数[12]：

(18)

通过式(18)能够对常量C进行求解∂CJ，得到：

(19)

规整化可信度参数λ(x,y)的表达式为式(18)。对噪声分布S(x,y)实施求解的具体过程为：预设噪声为加性高斯白噪声，含噪图像能够描述成：

u0=uc+uNC+un

(20)

式(20)内，uc、uNC、un分别表示轮廓图像、通过纹理和小尺度细节形成的残差图像以及加性高斯白噪声。那么残差图像uR能够描述成：

(21)

(22)

以上过程是基于参数P与λ的全变分图像自适应去噪算法运算原理分析部分，对基于参数P与λ的全变分图像自适应去噪算法实现图像去噪的具体步骤进行总结：

采用基于图像局部方向特性的自适应全变分去噪算法从含噪图像u0中分离出轮廓尺度图像u，获取的扩散迭代方程是：

λ(u-u0)

(23)

将获取的规整化可信度参数λ(x,y)代入基于参数P与λ的全变分图像自适应去噪算法运算原理部分，对含噪图像u0进行处理，获取最终的消噪图像，扩散迭代方程表示为：

λ(x,y)(u-u0)

(24)

2 实验分析

实验为了验证本文提出的基于能量回归滤波全变分图像自适应去噪算法的有效性，应用本文算法观察不同标准图像去噪后细节的保持情况，对不同标准图像去噪后的结果局部放大并与原含噪图像进行对比，对比结果如图1所示。

图1 APFTV去噪结果对比

通过对图1的分析可以得到：3个标准图像在使用本文算法进行去噪后，均实现了对噪声的消除，并且保留了更多的细节信息，说明采用本文算法能够有效的对图像进行去噪。

实验为了验证本文算法的去噪性能，使用包括本文算法和自适应非局部数据保真项和双边总变分的图像去噪算法在内的四种去噪算法对10个测试图像进行去噪试验[13]，并对去噪后的峰值信噪比进行对比，得到的结果见表1。

分析表1可以得到：与其他三种去噪算法相比较，使用本文算法对测试图像进行去噪后，峰值信噪比均高于其他三种算法。其中，对toys测试图像进行去噪时，使用本文算法得到的峰值信噪比比使用基于曲率差分的自适应全变分去噪算法高约0.5 dB[14]；对einstein图像进行去噪时，使用本文算法得到的峰值信噪比比使用基于自适应投影算法的分数阶全变分去噪算法高约1.9 dB[15]；对zelda图像进行去噪时，使用本文算法得到的峰值信噪比比使用自适应非局部数据保真项和双边总变分的图像去噪算法高约1.3 dB。实验结果表明，采用本文算法对图像进行去噪效果极佳。

实验为了验证本文算法的稳定性，采用“硬阈值”、“软阈值”和本文算法分别对噪声强度为30 dB、40 dB、50 dB的图像进行去噪处理，结果见表2。

经过对表2的分析能够得到：在噪声强度为30dB时，采用本文算法得到的峰值信噪比采用硬阈值算法高约1.7 dB；在噪声强度为40 dB时，采用本文算法得到的峰值信噪比采用软阈值算法高约1.8 dB；在噪声强度为50 dB时，采用本文算法得到的峰值信噪比采用软阈值算法和采用软值阈值的算法分别高约3.2 dB和0.5 dB。实验证明：采用本文算法对图像进行去噪，稳定性较高。

表1 不同去噪算法对10个测试图像去噪的峰值信噪比/dB

表2 不同阈值选择方法下三种噪声强度的图像去噪效果

实验为了验证本文算法的速度性能，采用本文算法及结合全变分的双边滤波图像去噪算法等4种去噪算法对8个测试图像进行去噪处理，将不同算法所用的时间记录下来并进行对比，对比结果如表3所示。

表3 不同去噪方法所花费的时间/s

通过上表能够看出，在对8个测试图像进行去噪处理时，与其他三种去噪算法相比较，采用本文算法去噪时使用的时间较短，则表明使用本文算法可以快速的对图像进行去噪处理。

3 结 语

文章提出了基于能量回归滤波全变分图像自适应去噪算法，很好的结合了能量回归滤波和全变分图像自适应算法，通过能量回归尺度空间滤波法获取滤波图像，在滤波图像的基础上采用基于参数P与λ的全变分图像自适应去噪算法最终实现图像去噪。解决了传统的基于图像局部方向特性的自适应全变分去噪算法在稳定性和去噪速度方面处在的问题，经实验证明本文算法能够快速、稳定的获取更高的风致信噪比，使人眼能够直观的感受到图像质量的提升,对于医学，工业及航天等诸多领域都有着极为重要的意义。