基于粒子滤波TBD的高机动目标检测技术

杨 帆,汪文英,王茹琪

(南京电子技术研究所，江苏 南京 210039)

0 引 言

高机动目标检测是高频雷达信号检测面临的难题之一。高频雷达采用相参体制、通过提高多普勒分辨率以改善强地海杂波和复杂外部电磁环境下的目标检测能力。对于相干积累时间内速度近似不变的空中目标，CIT的增加可有效提高目标信噪比；而机动目标在CIT内速度变化，其多普勒频率是时变的、回波信号相位非线性变化，相参积累后性能下降，表现为多普勒频谱展宽、信噪比降低[1]。目前针对弱机动目标的处理主要是将其建模为匀加速目标，采用匹配傅里叶变换法、多项式相位法以及多通道补偿法等检测。然而高加速、变加速等高机动目标，在相同的CIT内，自身的频谱展宽较弱机动目标要更为严重，信噪比损失更大，上述方法受模型失配以及算法鲁棒性等因素的影响，检测性能下降，需要结合新的信号处理技术减少积累损失，提高高机动目标发现概率。

检测前跟踪(TBD)技术是在低信噪比和复杂背景条件下对目标进行检测和跟踪的一种技术。高机动目标由于加速度导致信噪比积累损失，基于相参积累的检测方法性能下降。基于多帧积累思想的TBD技术利用目标运动的相关性对回波信号进行非相参积累，凸显目标信息的同时抑制杂波干扰，从而实现目标能量的有效积累、有效改善检测性能。本文将研究利用TBD技术解决高频雷达高机动目标检测问题。

1 粒子滤波TBD

检测前跟踪技术的主要算法为：动态规划法[2]、粒子滤波法[3]、霍夫变换法[4]等。其中粒子滤波TBD[3]技术对目标运动形式没有严格限制，适用于非线性、非高斯情况下的目标检测。针对本文所研究的问题，选择研究粒子滤波TBD算法在高机动目标检测中的应用。

1.1 粒子滤波器

粒子滤波是由英国学者Cordon,Salmond等于1993年提出来的，又称为序列重要采样法，是一种通过蒙特卡罗积分模拟来实现对贝叶斯滤波递推的技术[5]。检测方法是利用一序列随机样本(即粒子)的加权和表示所需的后验概率密度，并用新的量测数据来不断更新后验概率，得到状态的估计值。当粒子数很大时，此时概率估算将等同于后验概率密度，从而得到状态的估计值[5]。

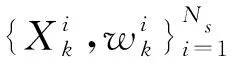
(1)

(2)

根据递归贝叶斯估计的思想，TBD问题被描述为：已知k-1时刻目标状态和目标存在状态的联合后验概率密度p(xk-1,Ek-1|Zk-1)，在得到最新观测数据zk的条件下，如何估计出k时刻的后验概率密度p(xk,Ek|Zk)。得到了后验概率密度函数p(xk,Ek=1|Zk)之后，目标的存在概率p(Ek=1|Zk)和目标的状态概率p(xk|Zk)都可以通过p(xk,Ek=1|Zk)的边缘概率密度计算得到。

1.2 标准SIR-TBD算法步骤

标准SIR-TBD(Sequential Importance Resampling-Track Before Detect, SIR-TBD)的核心是考虑将Ek变量加入所需估计的状态中去，参与状态估计过程，定义新的状态向量yk=[xkTEk]T。变量Ek表示目标是否存在，Ek∈{0,1}。目标的存在概率便可以通过这个指示目标存在与否的变量计算得到，即混合估计算法。算法具体流程如下：

a.粒子初始化

根据先验分布抽取N个随机样本，即粒子。

b.粒子的出生与死亡

假设第k帧有Na个粒子存活，随机选择NaPd个粒子死亡，将Ek置为零，选择(N-Na)Pb个粒子作为新出生粒子，Ek置1。

c.预测

第k帧新出生的粒子，进行如下抽样:

(3)

从第k-1帧存活下来的粒子，进行如下函数抽样：

(4)

d.更新

已经死亡的粒子，似然比函数值为1；

(5)

从k帧存活下来的粒子：

(6)

e.权值归一化

(7)

f.重采样

(8)

g.目标估计

目标状态估计公式为：

(9)

目标存在概率估计公式为：

(10)

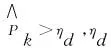
2 SIR-TBD检测高频雷达高机动目标

假设机动目标在距离-多普勒平面内运动，由于飞机目标速度变化快，因此考虑处理一个相干积累时间内的回波数据。将一个CIT内的数据分为多个小段数据，再进行分段相干积累，分成的数据段数根据雷达具体参数选择。假定每小段相干积累时间内目标速度近似不变(目标在该段时间内速度变化不超过5%)，各分段积累时刻间认为机动目标做近似匀加速运动，每个分段积累结果作为一帧观测数据。一般情况下变加速机动目标在一个相干积累时间内并不完全遵从变加速运动规律，同样假定它们在分段后的相干积累时间内速度近似不变，目标在分段积累时间段间做带有一定的加加速度扰动的匀变速运动，即可近似描述变加速目标的运动状态。

2.1 机动目标运动模型

假设某距离单元第k帧的目标状态为：

(11)

机动目标转移状态方程为：

Xk+1=FXk+EVk

(12)

其中：

(13)

(14)

2.2 观测模型

将分段相干积累所得到的K组数据作为K个连续时刻的观测数据：

(15)

3 实验结果

3.1 回波数据处理

图1为某帧回波数据频谱图和时频分析图，从该目标所在距离单元频谱图1(a)中可知其多普勒频谱有展宽，目标信噪比损失；此外结合对该数据的短时傅立叶变换分析图1(b)认为目标为机动目标，做近似匀加速运动，可以计算得出该机动目标平均加速度绝对值大于1 g，判断该目标为高机动目标。目标信噪比约为12 dB。

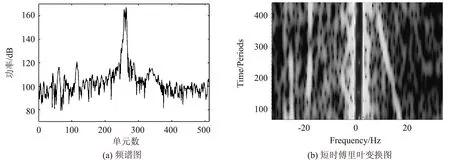
图1 某帧数据高机动目标分析图

图2 SIR-TBD对高机动目标的检测跟踪结果

从图2(c)可以看出，前两个时刻目标存在概率估计小于门限值0.6，其余时刻目标存在概率均大于ηd=0.6。检测结果出现时延是由于目标加速度太大，频谱展宽严重，信噪比有所降低引起的。多普勒及多普勒增量的估计理论值是根据时频分析的平均加速度计算所得，图2(a)中可见目标多普勒估计值与理论值基本相符，图2(b)中前几个时刻点多普勒增量与假定真实值存在少许偏差，但该偏差在允许范围之内。

根据SIR-TBD对该组回波数据的验证结果可知SIR-TBD受加速度范围的影响不大，对于信噪比满足一定条件、加速度值大于1 g的高机动目标具有较好的检测效果，同时能够较准确地估计出目标的运动参数速度和加速度，获取更为全面的目标信息。

3.2 检测性能曲线比较

为了更直观地比较粒子滤波TBD算法与常规机动目标处理的检测性能，考虑在回波数据中添加不同信噪比的机动目标，通过1000次蒙特卡罗实验得到虚警概率Pfa=10-3条件下，两种算法在相同虚警条件下的Pd-SNR关系曲线。其中常规机动目标处理采用性能较好的改进多通道补偿法。

SIR-TBD算法的检测概率Pd定义为：15个时刻内，目标估计概率大于门限ηd的时刻点数目大于等于10个，且目标检测时延小于等于3个时刻点的概率。图3为机动目标加速度a=10 m/s2，Pfa=10-3时两种算法Pd-SNR关系曲线。

图3 两种算法Pd-SNR关系曲线比较

由图3关系曲线对比看出，信噪比10 dB时，SIR-TBD算法获得的检测概率为87.5%，改进多通道补偿法获得的检测概率仅有9.7%。SIR-TBD算法受目标加速度范围影响较小，相比改进多通道补偿法可获得7 dB左右的性能改善，提高了高机动目标的检测性能。

4 结 语

本文针对高频雷达在高机动目标检测中存在的难题，提出基于粒子滤波SIR-TBD高机动目标检测算法。对回波数据的处理验证了该算法可成功检测加速度值大于1 g的高机动目标，并可获得较为精确的目标多普勒变化信息，有效抑制虚警。蒙特卡罗仿真表明，与常规机动目标检测方法相比，相同虚警概率条件下，SIR-TBD算法处理高机动目标可获得7 dB左右的性能提高。该方法经回波数据验证，具备一定的工程可行性。