基于PID和LESO的无人机控制

田 磊

(1.北京航空航天大学 自动化科学与电气工程学院，北京100191;2.北京航空航天大学 飞行器控制一体化技术国防科技重点实验室，北京100191)

0 引言

近年来，四旋翼无人机因体积小、质量小、易于操作等优点被应用于许多领域。视频拍摄、喷洒农药、消防灭火等都有无人机的身影，部分物流公司还提出无人机投放快递的构想，而对无人机控制方法的研究也一度成为控制领域的热点。

传统的PID控制方法设计简单，有一定的抗干扰能力，但当干扰较大时，实际值与期望值往往偏差较大，鲁棒性较差。滑膜变结构控制[1]具有很强的鲁棒性，能够克服系统的不确定性，对非线性系统具有很好的控制效果，但它的致命缺点是抖振现象，有时候会引起系统不稳定，甚至控制系统不可用。自适应控制[2]能够跟踪系统特性，感知系统变化，并实时修正控制参数，但其设计复杂，不易于实现。韩京清老师提出的自抗扰控制(ADRC)[3]既有PID的优点又结合了现代控制理论状态观测的优点。ADRC理论的核心是扩张状态观测器(ESO),可以估计系统所受到的扰动，并在控制器中进行补偿。而将非线性ADRC简化为线性，使ADRC的调整参数减少到3个，促进了ADRC 在工程上迅速推广和应用。

本文提出了一种基于PID和线性扩张状态观测器(LESO)的控制方法，将其应用到四旋翼无人机飞行控制中，并与传统PID控制方法进行对比，验证了自抗扰控制(ADRC)在无人机控制中有着抗干扰能力强、易于实现的优点。

1 四旋翼无人机的建模

如图1所示，四旋翼无人机通过4个电机带动4个旋翼提供升力，同时1、3和2、4这2对旋翼旋转的方向相反以平衡扭矩[4]。

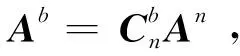
(1)

上述表达式明确了坐标系之间的转换关系，根据牛顿—欧拉方程，可以得到四旋翼无人机的动力学模型。

(2)

(3)

其中，F为机身所受的外力总和，m为机身质量，V为无人机在导航坐标系中的移动速度，记作[vxvyvz]T，M为机身所受到的力矩总和，Ω为机体坐标系下机体三轴角速度，记作[pqr]T，I为机身转动惯量矩阵，由于四旋翼无人机的对称布局特点可将其近似为一对角矩阵，记为I=diag[IxxIyyIzz]T。

若只考虑无人机自身的重力和旋翼产生的升力和扭矩，则

(4)

(5)

由文献[5]可知，四旋翼无人机的升力和扭矩与旋翼转速的平方成正比，即满足如下关系式：

(6)

其中，i∈{1,2,3,4}，分别代表编号1、2、3、4的4个旋翼，b为升力系数，d为扭矩系数。由此可知，四旋翼无人机的升力和扭矩可由控制旋翼的转速进行调节。因此系统的控制输入可定义为

(7)

由式(4)、式(5)可得

(8)

(9)

为了简化模型，将无人机在空间中的运动视为刚体运动，其在导航坐标系下的位置P定义为(x,y,z)，则无人机平动时的运动学方程为

(10)

而欧拉角Φ={φθψ}T与机体坐标系下机体三轴角速度Ω=[pqr]T之间的关系满足

(11)

将式(8)、式(10)代入式(2)，将式(9)、式(11)代入式(3)可得：

(12)

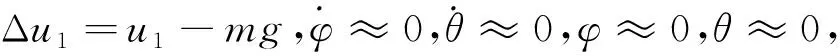
(13)

通过简化模型可得，高度z和欧拉角Φ={φθψ}T的控制实现了解耦，进而可以简化控制设计，在接下来的控制器设计中将以横滚角φ为例加以说明研究。

2 控制器的设计与仿真

若以横滚角φ为例，对于给定初始值φ0和扰动N，采用传统PID设计，系统结构图如图2所示。

其中，PID部分的数学模型[10]为

(14)

因为无人机的控制是通过调整旋翼转速实现的，所以控制改变的是角加速度，因此采用PD模型可以保证系统无静差，也不会出现积分环节I所带来的延时影响，将上述PID模型简化为PD模型，能够很好地满足控制要求。现采用在上述PID控制器的基础上增加LESO的设计方法[11-15]，可得系统结构图如图3所示。

其中，LESO部分的数学模型[16]为

(15)

A、B、C与被控对象中的取值相同，H为需要设计的观测器增益矩阵，参数化处理后，观测器的增益矩阵为

其中，ω0为观测器带宽。因此观测器的特征方程为

|sI-A+HC|=(s+ω0)3

(16)

可得特征方程的极点都配置在s=-ω0处，进而使LESO的设计变得简单。

取给定值φ0为如图4所示的正弦信号。

扰动N为如图5所示的平稳信号。

进而可得传统PID方法的仿真结果如图6所示，加入LESO的仿真结果如图7所示，其中实线代表横滚角给定值，虚线代表横滚角实际值。

由图6和图7可以明显看出，加入LESO后无人机横滚角曲线的跟随效果较好。由图8可知，传统PID方法的误差值一直在10°以内并随干扰上下波动。而由图9可知，加入LESO后的误差值可以缩小到2°以内，最终稳定到0.5°以内。综上所述，加入LESO的控制器使得无人机在飞行过程中抗干扰效果更好。

3 实际无人机飞行数据对比

上述仿真结果显示，加入LESO的抗干扰效果非常理想，进而在实际飞行中进行验证。分别收集采用PID控制方法和采用PID和LESO组合控制方法的无人机飞行数据，如图10、图11所示，其中实线代表横滚角给定值，虚线代表横滚角实际值。计算扰动后横滚角的误差值，如图12、图13所示。由图12可知，传统PID方法的误差值一直在10°左右；而由图13可知，加入LESO后的误差值可以缩小到2°以内，实际飞行与仿真得到的结论基本一致。综上所述，自抗扰控制(ADRC)用于无人机控制产生了非常良好的干扰抑制效果。

4 结论

本文基于传统PID控制方法，加入线性扩张状态观测器(LESO)，提出一种干扰抑制的改进方法，并将其应用在无人机飞行控制中。通过仿真和实际飞行验证，证明了该方法具有良好的干扰抑制特性，设计相对简单，效果理想，是一种可行并实用的控制方法。