一种基于动态挠曲误差估计的“速度+姿态”传递对准方法

任晓军，刘 冲，李海军，原 润，裴玉锋

(1.海军驻某院军事代表室，北京 100074；2.北京自动化控制设备研究所，北京 100074)

0 引言

舰艇主基准安装于舰艇船舱内的固定位置，安装位置离全舰安装的各型武器距离较远，输出信息无法准确表征武器所在位置的航姿信息，为了保证导弹武器系统能够利用准确的信息完成发射前的装订对准工作，就需要利用武器安装位置处的航姿基准(子基准)，以保证传递对准信息的可靠性及准确性。

由于子基准离舰艇主基准距离较远，舰艇的挠曲变形对主子基准之间的传递对准影响不可忽略，特别是对姿态匹配过程的影响，因此在早期应用中一般采用速度匹配方式进行传递对准。但是速度匹配缺点明显，误差收敛较慢，且短时间内无法估计对系统精度有较大影响的陀螺漂移误差，所以对姿态匹配算法的需求依旧十分迫切[1]。

因此，为了保证主子基准之间的传递对准精度，最大程度降低舰艇挠曲变形的影响，本文通过对舰艇挠曲角及挠曲角速率的建模分析，设计合理的误差模型即二阶马尔可夫过程，提高主子基准间安装误差及惯性器件误差的估计精度，进而提高姿态匹配精度[2]。

1 坐标系定义

1.1 坐标系定义

1)地理坐标系n

地理坐标系采用北天东坐标系，即n系ONUE。

2)导航坐标系n′

系统导航坐标系采用地理坐标系，计算导航坐标系记为n′系。

3)惯导体坐标系b

惯导体坐标系取为前上右坐标系，且X轴与X加速度计敏感轴重合，Y轴与X轴垂直指右且在X和Y加速度计敏感轴组成的平面内，Z轴与X、Y轴构成右手系，即b系OXbYbZb。

4)主基准体坐标系m0

假定主基准输出的航姿坐标也采用地理坐标系为导航系，主基准体系为m0系，即OXm0Ym0Zm0，其方向与惯导体坐标系大致一致。

5)虚拟主基准坐标系m

将主基准坐标系m0经过标校值转换到b系附近，得到虚拟主基准坐标系m。

6)舰艇基准坐标系J

舰艇基准坐标系定位为J系。该坐标系为要求子基准输出的坐标系，一般为舰艇艏艉线和水平基准面构成的正交坐标系，航向为艏向。如果要求子基准输出航姿到附近的基准平面镜和基准水平面上，则舰艇上基准坐标系为该基准平面镜法向和水平面构成的正交坐标系上。

7)子基准坐标系J1

子基准上的棱镜与内部水平基准面构成的坐标系J1，航向为棱镜法向方向。

1.2 坐标系间转换关系

1)地理坐标系n

2)J系到J1系

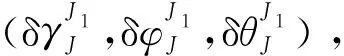
3)J1系到b系

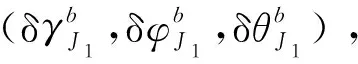
4)m0系到J系

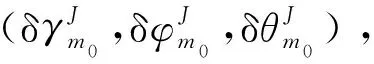
5)m0系到b系

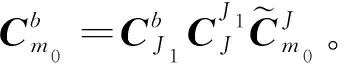
(1)

6)m系到b系

假设m系到b系的滚航俯安装误差角为(γerr,φerr,θerr)，其中安装误差角方向的定义与导航内部姿态角定义一致。于是可得m系到b系安装误差矩阵为

(2)

当其间安装误差角为小角度时，即为φa=[φaX

φaYφaZ]T，其中φaX≈γerr，φaY≈φerr，φaZ≈θerr，则式(2)可写为

(3)

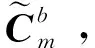
7)m系到n系

(4)

2 挠曲特性分析及建模

受运动方式、环境干扰等方面因素的影响。载体运动带来的挠曲变形是影响姿态匹配过程的重要因素。研究表明，舰艇结构挠曲变形可产生1°以上的失准角。

目前常用的速度匹配传递对准方法，受挠曲变形影响较小，但是速度匹配无法快速估计陀螺漂移误差，且误差估计精度稍差，无法满足高精度光学陀螺惯导系统的应用需求。

通过对挠曲变形的深入研究发现，载体的动态挠曲变形模型受载体类型、运动条件、参数、外在环境等诸多因素的影响，建立准确模型十分困难。载体挠曲变形是随机扰动量，与白噪声驱动的二阶马尔可夫过程类似。因此，选用二阶马尔可夫过程作为载体动态挠曲变形的模型，并且认为各个轴向的挠曲变形是相互独立的[4]。

挠曲变形的二阶马尔可夫过程公式如下：

(5)

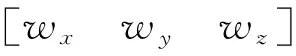
3 Kalman滤波误差模型

在现有“速度+姿态”匹配误差模型基础上增加6维挠曲误差量，包括3个挠曲角误差，3个挠曲角速率，误差量增加到24维，具体为

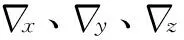
系统状态方程为

其中，A为系统矩阵，其表达式为

A1为依据误差模型确定的标准表达式，不再赘述。而A2表达式如下

A2=

其中：βx=βy=βz=2.146/τ，τ为时间常数，这里定为5.0。

与挠曲误差相关的状态估计阵P及噪声阵Q的初始值为

P0=diag[(0.1°)2、(0.1°)2、(0.1°)2、(0.1°)2、

(0.1°)2、(0.1°)2]

舰艇在风浪冲击条件下的挠曲角度及挠曲角速率均为小值，同时分析实际舰载试验数据，确定了一个较为通用的挠曲误差角的P阵初值[5]。

Q0=diag[Qx、Qy、Qz]

其中：

舰艇在不同风浪冲击条件下，挠曲变形的大小会出现细微差异，而通过实际舰载数据处理分析发现，舰艇的挠曲变形误差会随着舰艇角速度的变化而变化[6]。因此，为了提高误差模型对不同海域不同海情的适应性，将与挠曲误差对应的Q阵相应元素进行自适应调整，其值与舰艇角速度相关。同时为了消除随机误差的影响，计算出舰艇角速度的1s均值，而进一步分析发现，3个方向的挠曲误差量与3个角速度的合成量相关。通过对不同海域不同海情下的舰载数据分析，最终确定了Q阵元素的自适应调整方案[7]。

通过P、Q阵的合理设置能够利用Kalman滤波过程分离估计主子基准之间的挠曲误差，提高主子基准之间安装误差及惯性器件误差的估计及收敛精度，提高主子基准间传递对准精度，保证子基准系统输出信息的可靠性[8]。

4 舰载数据验证

为了验证动态挠曲误差估计方法的有效性及正确性，对实际系统的舰载试验数据进行仿真处理。

首先给出实际舰载试验过程中3个方向舰艇挠曲误差的估计曲线，如图1～图3所示。

从图中可以看出，挠曲误差为高频小量级的误差量，此类误差与随机游走误差类似，会严重影响零偏的估计精度与收敛效果[9]。通过在模型中增加挠曲误差模型，将有害的挠曲误差量隔离出来，增加惯性器件误差的估计精度与收敛效果[10]。

下面给出了有无挠曲误差模型条件下惯性器件误差的估计曲线，加表零偏估计曲线如图4所示(两种情况下天向加表零偏估计曲线基本重合)，陀螺漂移估计曲线如图5所示[11]。

从图4曲线可以看出，增加动态挠曲误差模型之前，在0～1000s估计出错误的水平加表零偏，而后又缓慢收敛到准确值[12]；而增加挠曲误差模型后，水平加表零偏不会出现异常发散，而且收敛曲线更加平稳，由此说明加入挠曲误差模型后水平加表零偏的估计效果明显提高。从曲线还可以看出，两种条件下天向加表零偏的估计曲线无明显变化[13]。

从图5曲线可以看出，增加动态挠曲误差模型之后，陀螺漂移估计值缓慢收敛到真值附近，而不会出现大幅振荡，收敛平稳性明显提高[14]。

从图4、图5曲线可以看出，加入挠曲误差模型之后惯性器件误差的估计效果明显提高。目前该方法已在多个项目中成功应用[15]。

5 结论

通过在“速度+姿态”匹配传递对准模型中增加动态挠曲误差模型，可以分离估计主子基准之间的挠曲误差，能够完成失准角的可靠修正，提高主子基准之间安装误差及惯性器件误差，特别是陀螺漂移的估计及收敛精度，提高主子基准间传递对准精度，保证子基准系统输出信息的可靠性。