利用多目标PSO优化的累积时延和信道容量联合优化的频谱切换算法

2018-07-23张煜培赵知劲郑仕链

电信科学 2018年7期

张煜培，赵知劲，郑仕链

张煜培1，赵知劲1,2，郑仕链2

（1. 杭州电子科技大学通信工程学院，浙江杭州 310018;2. 中国电子科技集团第36研究所通信系统信息控制技术国家级重点实验室，浙江嘉兴 314001）

目前频谱切换中多以单目标优化设计目标信道，为了满足大容量实时传输要求，需要综合考虑累积切换时延和有效信道容量。对此构建了目标信道设计的多目标函数，提出了求解离散多目标优化问题的粒子群算法（DMOPSO），给出了种群编码、更新方式离散化设计。仿真结果表明，所提出的频谱切换算法得到的最优信道访问解集能够兼顾网络的实时性和高吞吐率，算法复杂度较低。

多目标优化；频谱切换；累积时延；信道容量；粒子群优化

1 引言

无线设备的快速增长导致频带接入需求急剧增加，而美国联邦通信委员会（Federal Communications Commission，FCC）的调查表明，高达85%授权频谱未被充分利用[1]。认知无线电（cognitive radio，CR）是一种解决频谱利用率低下和日益增长的频谱接入需求之间矛盾的技术，认知用户（secondary user，SU）在空时变化的无线电环境中寻找频谱空穴，自适应调整自身参数，机会式接入未被主用户使用的授权频带[2]。为了不影响主用户（primary user，PU）通信，当认知用户使用的信道中突然出现优先级高的PU时，认知用户必须离开当前信道，寻找新的空闲信道，以保证通信的连续性，这一过程即频谱切换[3]。频谱切换是认知无线网络的关键技术之一[4]。

目标信道对频谱切换来说至关重要，因为目标信道是通信得以维持的希望。目前，按照目标信道序列的长度，可以将其分为3类：1个目标信道、2个目标信道和2个以上目标信道。参考文献[5]基于动态规划选择剩余空闲时间最长的一个信道作为目标信道。参考文献[6]提出一种混合主被动频谱切换的频谱切换算法，考虑非理想检测对切换的影响，选择累积切换时延最小的一个信道。参考文献[7]提出将保护信道作为备用信道，频谱切换时，如果有空闲信道就切换到空闲信道，否则切换到保护信道，以切换时延最短为衡量标准。参考文献[8]提出一种基于抢占式续传优先权//排队理论的频谱切换模型，以传输时间为评价标准。可是这些算法目标信道只有1个或2个，存在很大的切换失败风险。参考文献[9-10]选择多个目标信道，其中，参考文献[9]提出一种结合动态规划与二分法（DPB）算法，以降低能耗为衡量标准；参考文献[10]仿真了目标信道长度分别为5、6、7和8时的切换时延，提出按信道空闲时间排序，使得累积切换时延最小。

以上参考文献主要从单个角度衡量频谱切换性能，然而实际切换过程中，信道容量也是一个很重要的参考因素，即使切换次数很少，如果信道容量较小，也无法满足认知用户的通信需求。目前只有少数文献涉及这方面工作，参考文献[11-12]以最大化系统吞吐量为衡量标准，参考文献[11]只有1个目标信道和1个备用信道，仍存在较大的切换失败概率。参考文献[12]提出分组传输思想以最大化吞吐量，但未考虑平均累积时延的影响。参考文献[13]提出利用加权方式将信道容量和切换失败概率同时优化，但是它们对于权重或目标给定次序较敏感，并且权重并不能准确反映用户优化需求。

针对上述问题，本文在先应式感知频谱切换环境[12]中引入累积切换时延和有效信道容量作为频谱切换的评价标准，选择目标信道序列，以降低切换失败概率。这是一个多目标优化问题，传统穷举算法搜索所有目标信道排列，导致复杂度高。MOPSO[14]是一种经典的解决多目标优化的进化算法，但这种算法用于解决连续域优化问题，而本文的自变量是信道访问顺序，是离散的。因此本文提出离散多目标粒子群优化（discrete multi-objective particle swarm optimization，DMOPSO）算法解决本文构建的多目标优化问题，得到频谱切换算法。该算法复杂度低，能够兼顾网络的实时性和高吞吐率。

2 频谱切换优化模型

2.1 问题描述

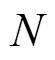
2.2 频谱切换失败概率

假设信道空闲时间服从指数分布[10]，信道空闲时间概率密度函数为：

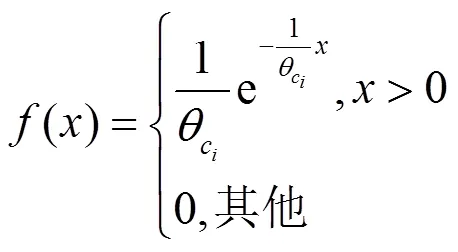
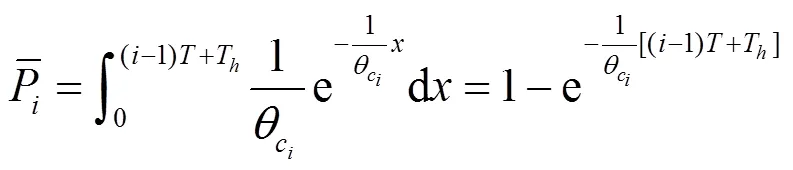
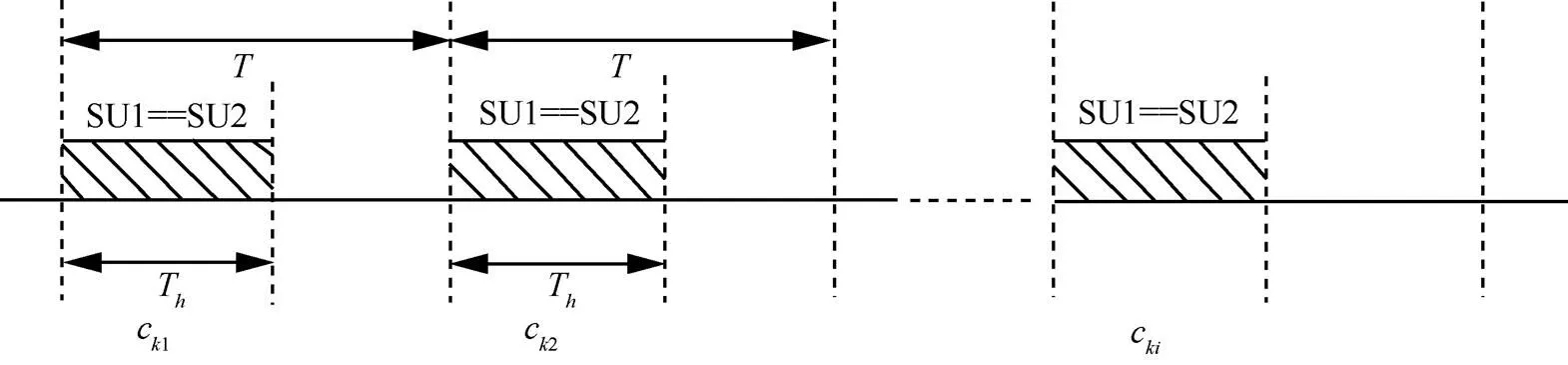
图1 频谱切换示意

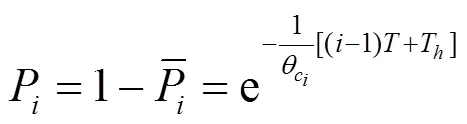
则本次频谱切换失败的概率为：

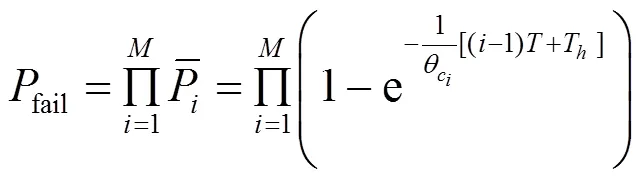
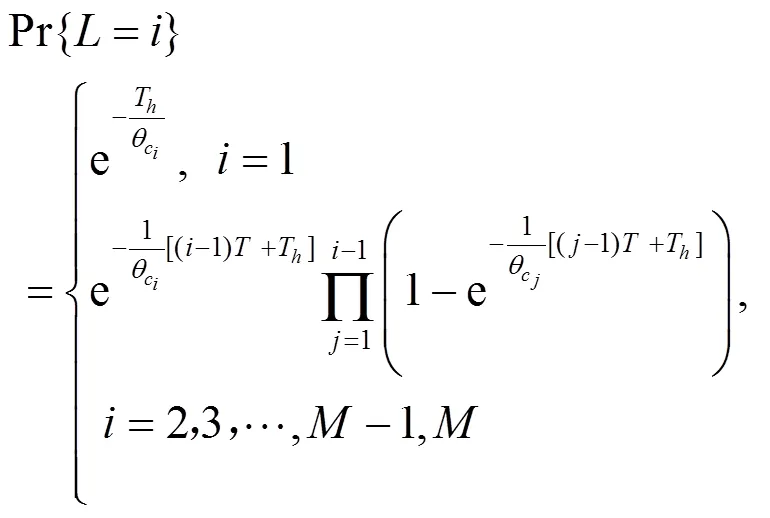
2.3 累积切换时延

由第2.1节和第2.2节的分析可知，累积切换时延（ACHD）由两部分构成，一部分是切换成功时产生的时延，另一部分是切换失败时产生的时延，其衡量本次切换过程中平均消耗时间，累积切换时延[6,10]为：

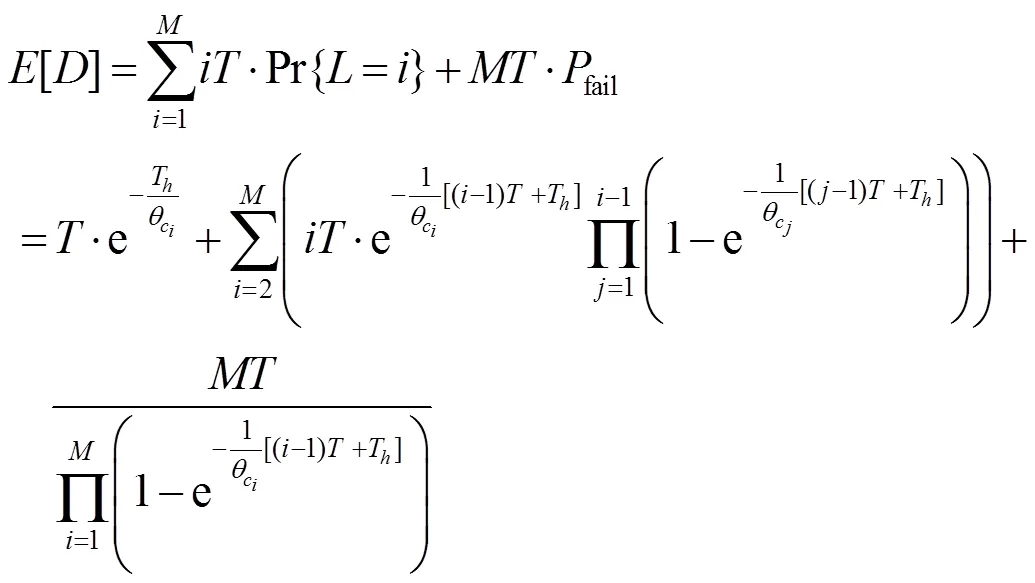
2.4 有效信道容量

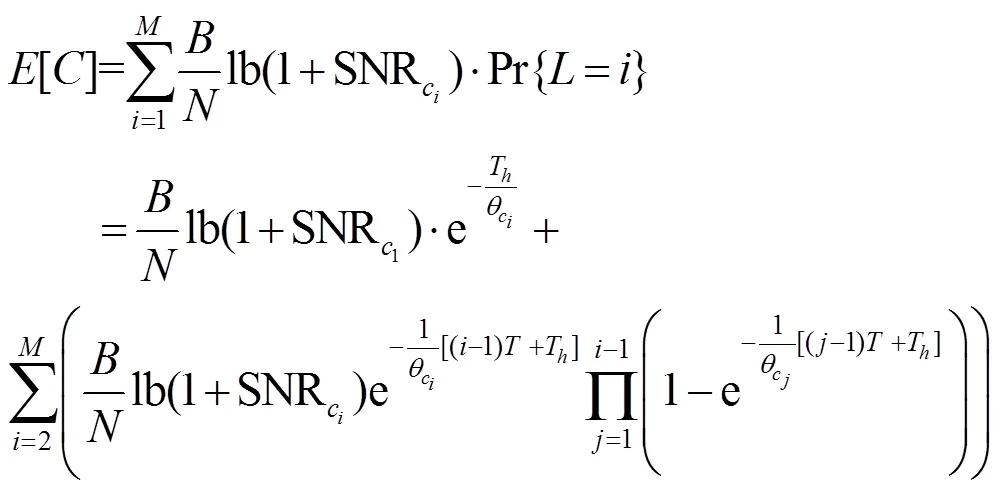
2.5 目标函数设计

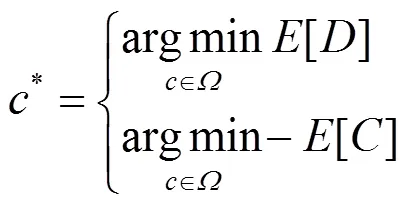
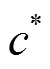
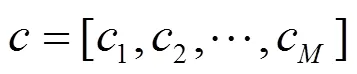
定义2 Pareto前沿（Pareto front，PF）：所有互不支配的信道解集构成Pareto最优解，这些最优解集在目标空间形成Pareto前沿。

3 频谱切换算法

3.1 MOPSO算法

Coello于2004年提出了经典的求解多目标问题的粒子群优化算法MOPSO，该算法引入外部档案Archive并应用自适应网格法维护Archive中的非支配解[14]，算法主要步骤描述如下。

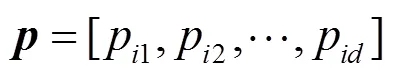
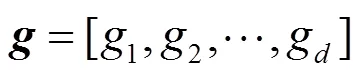
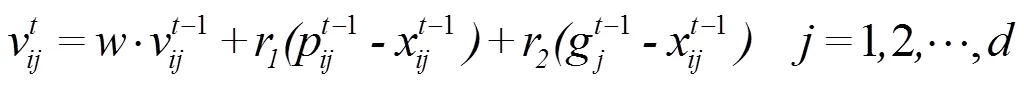
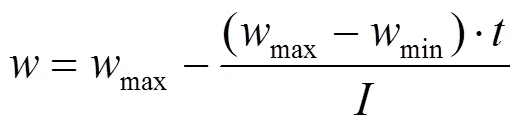
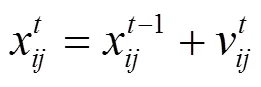
步骤4 计算每个粒子的目标函数值实现的更新。

步骤5 更新。根据粒子飞行过程中获得的当前解和上次的比较，若当前解支配，令当前解为；若二者互不支配，则从二者之间随机选择一个作为。

步骤6 如果终止条件成立，输出Archive集，否则转步骤2。

3.2 DMOPSO算法

由于MOPSO主要应用于连续域情况，本文自变量是信道访问顺序，是离散的，因此需要对编码方式和位置更新式离散化，以适用于频谱切换优化问题。

3.2.1 编码

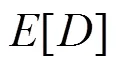
3.2.2 离散位置更新

由式（11）可知，在连续域中，位置更新是通过本次的速度值加上次的位置值实现的，但在本文中，位置值只能在“0”或“1”中选取，参考文献[16]提出利用Sigmoid函数进行位置更新，如式（13）所示，思想是将粒子速度作为其位置更新的概率，该函数表达式及图形如式（12）和图2（a）所示。

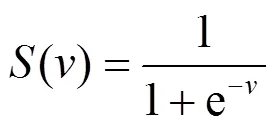
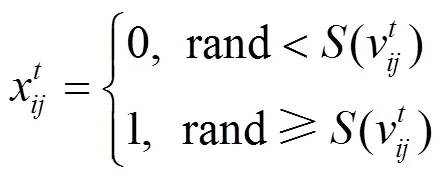
该函数虽然将位置值约束到[0,1]上，但当速度负向增大时，其位置改变的概率趋近于0，这不合常理，本文引入“V”型函数[18]，如图2（b）所示，该函数不仅将速度值约束到[0,1]上，而且满足当速度的绝对值较小时，其位置改变概率小，当速度绝对值较大时，其位置改变概率也较大。因此本文使用式（15）进行位置更新。

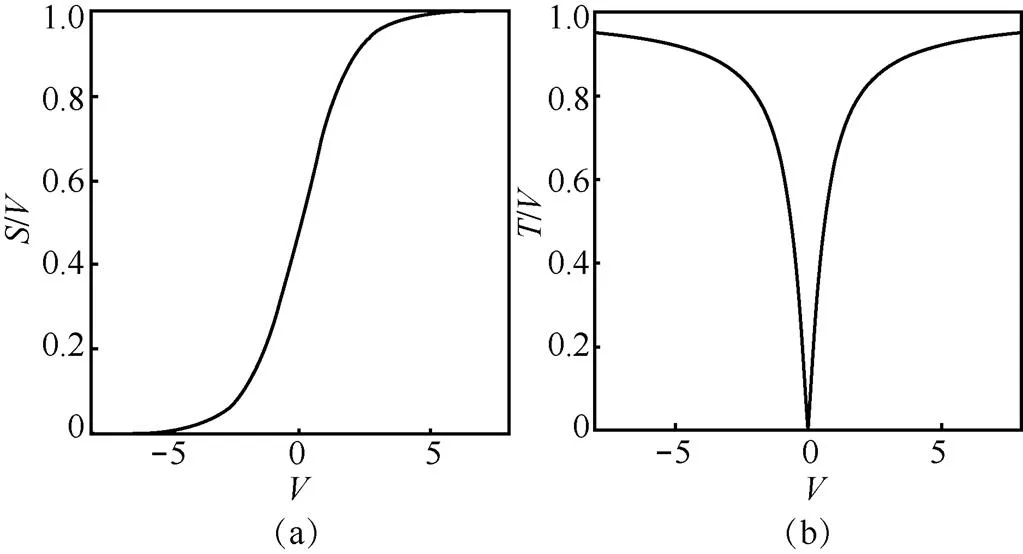
图2 Sigmoid函数和V型函数图像

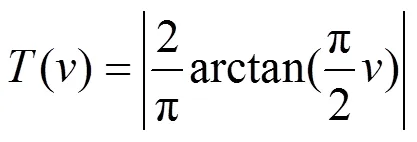
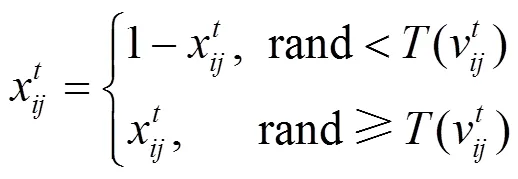
3.2.3 最优值更新

3.3 频谱切换算法主要步骤

将上述离散多目标优化算法应用于本文切换优化模型，就得到本文提出的频谱切换算法，仍记为DMOPSO，主要步骤描述如下。

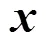
步骤6 输出Archive集中的非支配解集（PF前沿）作为结果集。

4 算法仿真与性能分析

4.1 参数设置

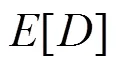
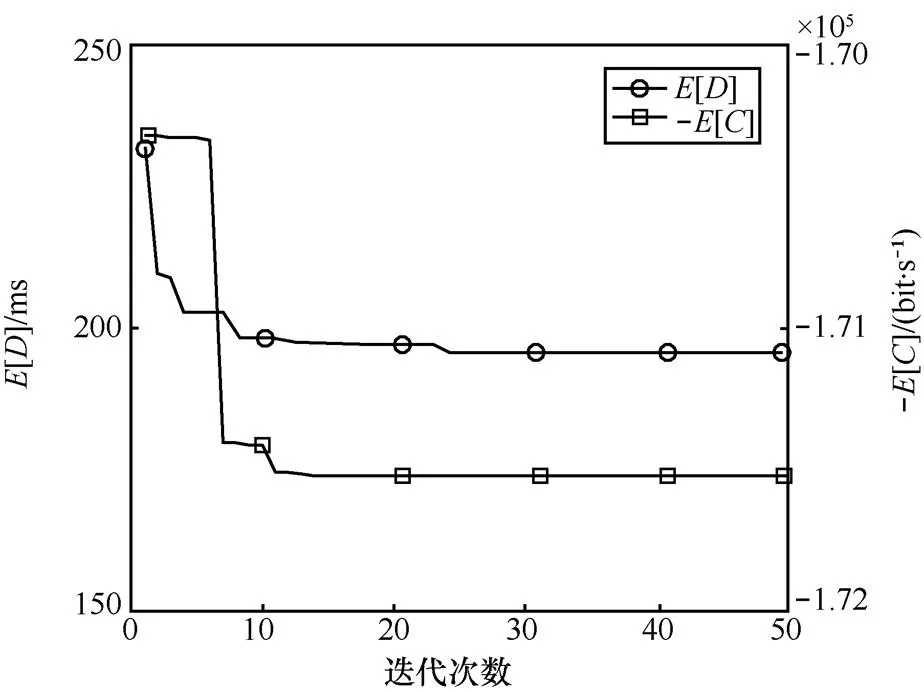
图3 和随迭代次数变换曲线

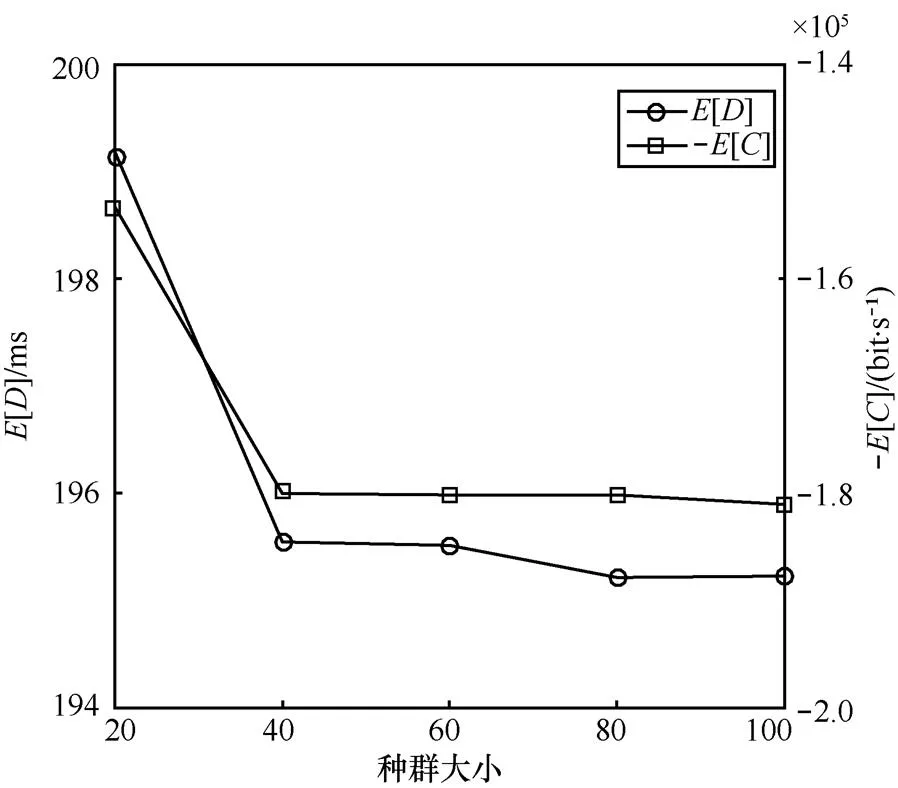
图4 和随种群大小变换曲线

4.2 频谱切换性能分析

4.2.1 寻优性能

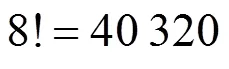
2种算法求解得到的Pareto前沿（PF）分别如图5和图6所示。标有“□”的表示错误的Pareto最优解。由于本文中目标函数不连续、不可微也不可导，因此得到的最优解集是零散的点，但是可以看出，2种算法能较好地逼近理论的Pareto前沿，说明2种算法应用于本文切换模型都是有效的。同时可以看出“V”型函数相较于Sigmod函数，增大了位置变化的概率，搜索能力更强。

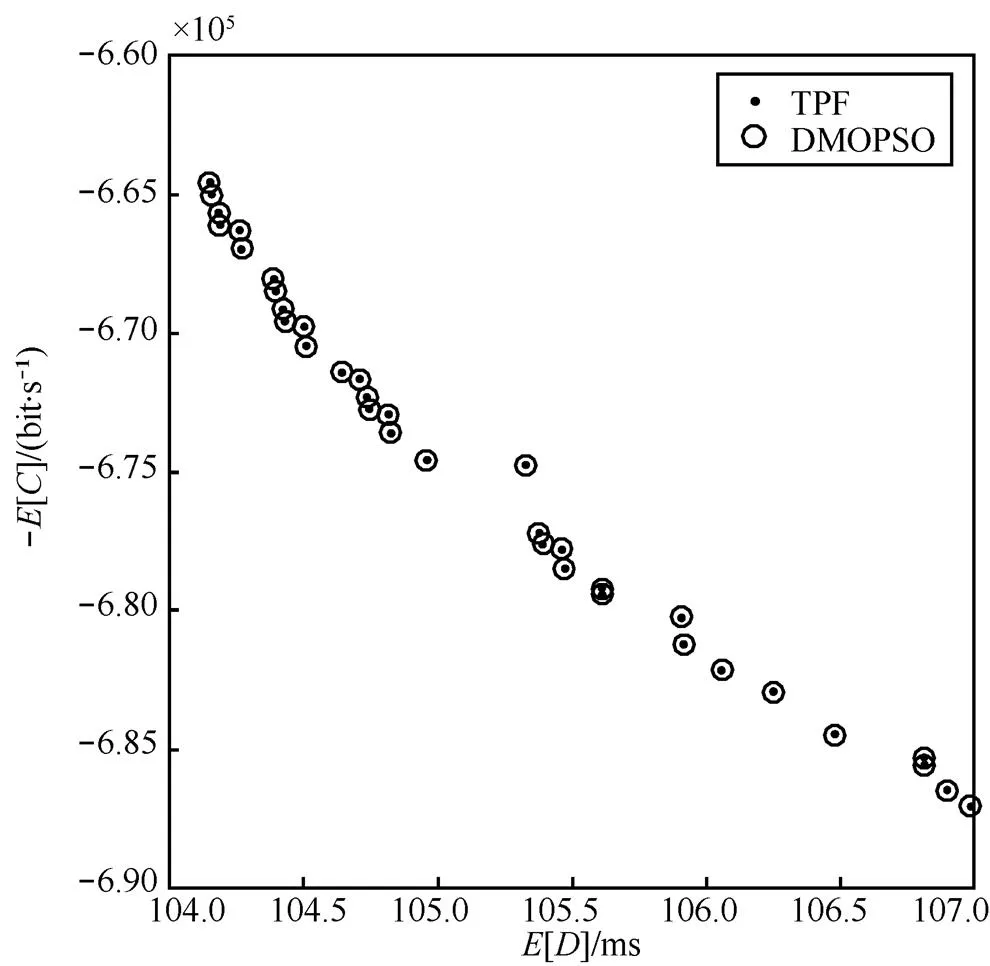
图5 DMOPSO算法求得的PF

图6 DMOPSO-S算法求得的PF

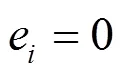
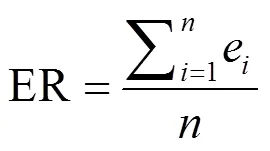
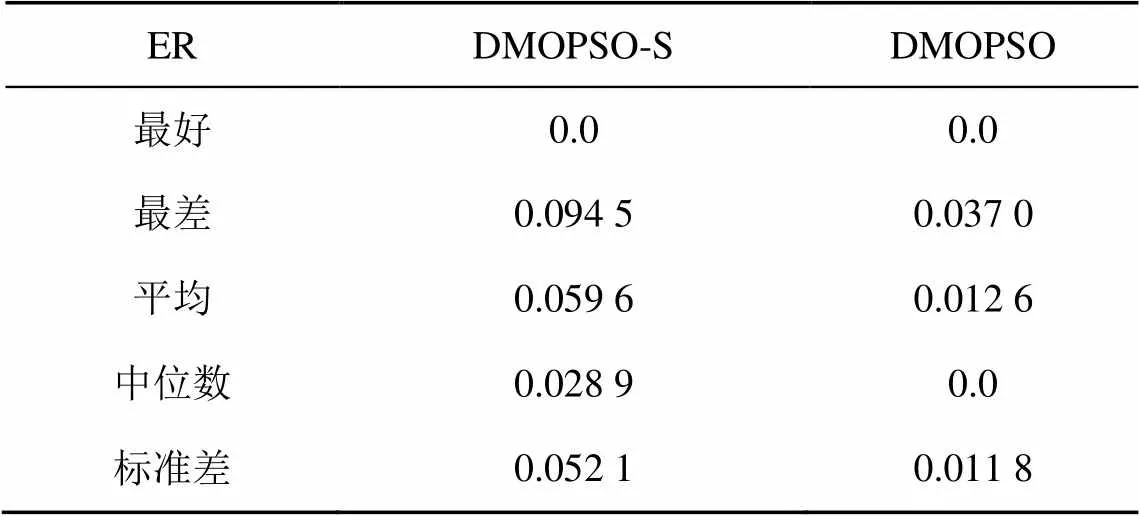
表1 两种算法的错误率

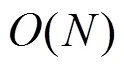
4.2.2 频谱切换性能

下面分析DMOPSO算法的频谱切换性能，并与最小切换时延算法[10]、基于最大信道容量算法[13]和随机顺序访问算法[17]进行比较。

图7给出了初始化的粒子群和DMOPSO算法得到的最优信道解集在目标空间的分布。由图7可以看出，初始化的粒子种群能够在目标空间内近似均匀地分布，这为寻找最优信道解集提供了保证。经过30次迭代后，本文算法最终得到的最优信道解集在图7的左下方，其中每个点代表了一种信道访问序列，任意的两个点都在一个目标函数上优于另一个点，而在另一个目标函数上劣于另一个点。为了方便以下讨论，将本文算法得到的最优信道解集依次编号为1～10。

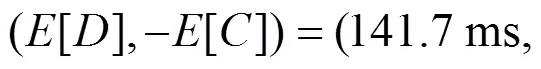
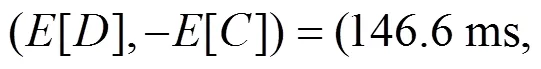
表2 DMOPSO相较于参考文献[10]在信道容量增加量和时延减少量百分比

表3 DMOPSO相较于参考文献[13]在信道容量增加量和时延减少量百分比

表4 DMOPSO相较于参考文献[17]在信道容量增加量和时延减少量百分比

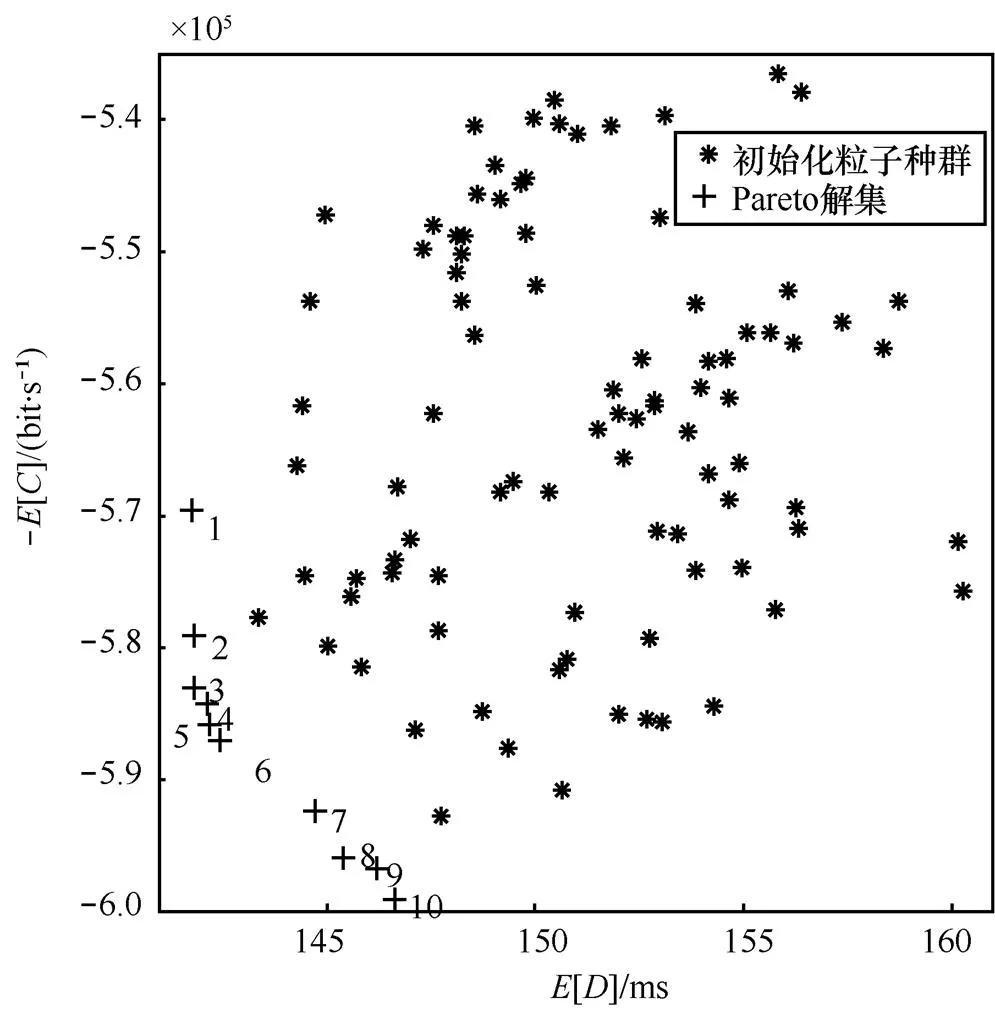
图7 Pareto最优解及初始化种群在目标空间的分布

为了衡量DMOPSO算法和随机顺序访问算法[17]性能，随机选取各信道空闲时间（）和信噪比（SNR），以参考文献[17]算法得到的结果为参考，图7中各个编号的结果与之对比，得到的目标函数值增减量见表4。随机顺序访问算法虽然时间复杂度很低，但是本文DMOPSO算法的信道容量高于其24%以上，时延降低8%以上。

分析DMOPSO、参考文献[10]、参考文献[13]和参考文献[17]4种算法的切换失败概率[15]。计算得到参考文献[10]、参考文献[13]和参考文献[17]的切换失败概率分别为0.004 7、0.005和0.011 8，DMOPSO算法的10个最优信道解集所对应的切换失败概率如图8所示，表5给出了参考文献[10]、参考文献[13]和参考文献[17]相对DMOPSO算法的10个最优信道解集的切换失败概率减小百分比（0表示二者切换失败概率相同）。

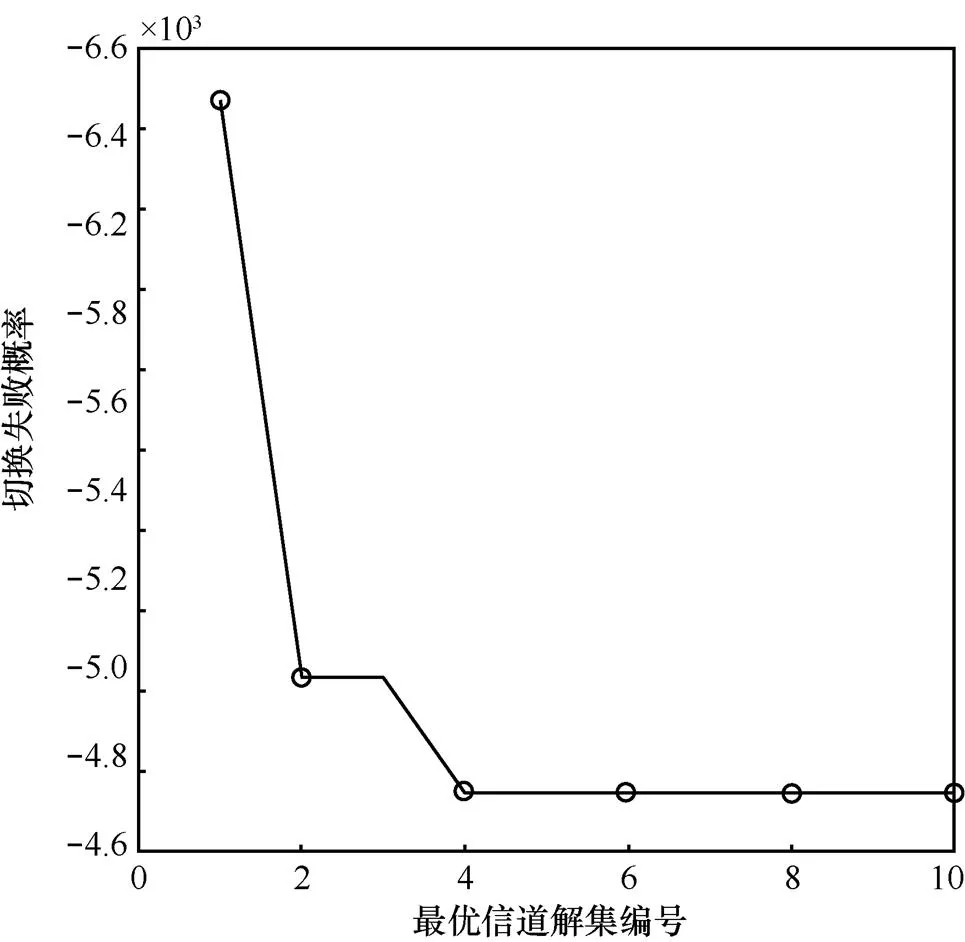
图8 最优信道解集对应的切换失败概率

由表5可知，参考文献[10]、参考文献[13]和DMOPSO算法的失败概率均较小，说明3种算法的有效性；参考文献[17]的随机顺序访问算法的失败概率较高；参考文献[10]算法虽然能达到最小的失败概率，但是该算法未考虑切换时延，而本文算法编号3以后的最优信道解集的访问顺序能达到和参考文献[10]同样低的失败概率；本文算法编号2以后的最优信道解集的访问顺序的失败概率都比参考文献[13]算法的小，而且参考文献[13]算法未考虑切换时延。所以相比较而言，本文算法能同时兼顾较小切换时延、较高信道容量和较低切换失败概率。

表5 DMOPSO算法的切换失败概率相对参考文献[10]、参考文献[13]和参考文献[17]减小百分比

5 结束语

频谱切换是主用户和认知用户维持自身通信质量的关键技术之一。目前频谱切换中目标信道的设计方法大多只引入单个切换性能度量，难以满足实际需求，为此，本文综合考虑信道容量和切换时延两个性能指标要求；同时为了降低复杂度，提出离散多目标粒子群算法。仿真表明所提算法能够很好地求解离散多目标优化的频谱切换问题，同时兼顾了网络的实时性和高吞吐率。

[1] LALA N A, UDDIN M, SHEIKHC N A. Novel hybrid spectrum handoff for cognitive radio networks[J]. International Journal of Wireless & Microwave Technologies, 2013, 3(1): 1-10.

[2] 冯岩, 孙浩, 许颖, 等. 动态频谱共享研究现状及展望[J]. 电信科学, 2016, 32(2):112-119.

FENG Y, SUN H, XU Y, et al. Review and prospect on the research of dynamic spectrum sharing [J]. Telecommunications Science, 2016, 32(2): 112-119.

[3] TIWARI K, RASTOGI A. Spectrum handoff in cognitive radio network[J]. International Journal of Advanced Research in Computer Communication Engineering, 2016, 5(4): 1025-1030.

[4] 张平, 李建武, 冯志勇, 等. 认知无线网络基础理论与关键技术研究[J]. 电信科学, 2014, 30(2): 1-13.

ZHANG P, LI J W, FENG Z Y, et al. Research on basic theory and key technology of cognitive radio network [J]. Telecommunications Science, 2014, 30(2): 1-13.

[5] ZHANG W, CHAI K Y. Sequential sensing based spectrum handoff in cognitive radio networks with multiple users[J]. Computer Networks, 2014, 58(1): 87-98.

[6] 马彬, 包小敏, 谢显中. 认知无线网络中基于混合频谱切换的最优目标信道选择算法[J]. 电子与信息学报, 2017, 39(1): 31-37.

MA B, BAO X M, XIE X Z. Optimal target channel selection algorithm based on hybrid spectrum handoffs in cognitive radio networks[J]. Journal of Electronics & Information Technology, 2017, 39(1): 31-37.

[7] ZAHED S, AWAN I, CULLEN A. Analytical modeling for spectrum handoff decision in cognitive radio networks[J]. Simulation Modelling Practice & Theory, 2013, 38(1): 98-114.

[8] 杨小龙, 谭学治, 关凯. 认知无线电网络中基于抢占式排队论的频谱切换模型[J]. 物理学报, 2015, 64(10): 108403.

YANG X L, TAN X Z, GUAN K. Spectrum handoff model based on preemptive queuing theory in cognitive radio networks[J]. Acta Physica Sinica, 2015, 64(10): 108403.

[9] YANG X, TAN X. Energy-efficient target channel sequence design for spectrum handoffs in cognitive radio networks[J]. China Communications, 2017, 14(5): 207-217.

[10] ZHENG S, YANG X, CHEN S, et al. Target channel sequence selection scheme for proactive-decision spectrum handoff[J]. IEEE Communications Letters, 2011, 15(12): 1332-1334.

[11] USMAN M, KHAN M S, VUVAN H, et al. Energy-efficient channel handoff for sensor network-assisted cognitive radio network[J]. Sensors, 2015, 15(8): 18012-39.

[12] KUMAR K, MISHRA G P, PRAKASH A, et al. A proactive spectrum handoff scheme with efficient spectrum utilisation for cognitive radio ad hoc networks[J]. International Journal of Internet Protocol Technology, 2017, 10(3): 160.

[13] 许蒙迪, 金明, 童景文. 一种基于切换失败概率和认知用户信道容量联合优化的访问策略[J]. 电信科学, 2016, 32(9): 82-88.

XU M D, JIN M, TONG J W. A channel visiting strategy based on joint optimization of probability of handoff failure and capacity of secondary user[J]. Telecommunications Science, 2016, 32(9): 82-88.

[14] COELLO C A C, PULIDO G T, Lechuga M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256-279.

[15] 郑仕链, 杨小牛. 认知无线电频谱切换目标信道访问机制[J]. 电子与信息学报, 2012, 34(9): 2213-2217.

ZHENG S L, YANG X N. Target channel visiting scheme for spectrum handoff in cognitive radio[J]. Journal of Electronics & Information Technology, 2012, 34(9): 2213-2217.

[16] KENNEDY J, EBERHART R C. A discrete binary version of the particle swarm algorithm[C]// IEEE International Conference on Systems, Man, and Cybernetics, October 12-15, 1997, Hyatt Orlando, Orlando, Florida, USA. Piscataway: IEEE Press, 1997: 4104-4108.

[17] SHOKRI-GHADIKOLAEI H, FISCHIONE C. Analysis and optimization of random sensing order in cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(5): 803-819.

[18] MIRJALILI S, MIRJALILI S M, YANG X S. Binary bat algorithm[J]. Neural Computing & Applications, 2014, 25(3-4): 663-681.

Spectrum handoff method by using joint optimization of cumulative delay and channel capacity based on multi-objective PSO

ZHANG Yupei1, ZHAO Zhijin1,2, ZHENG Shilian2

1. School of Telecommunication Engineering, Hangzhou Dianzi University, Hangzhou 310018, China 2. State Key Lab of Information Control Technology in Communication System of No.36 Research Institute, China Electronic Technology Corporation, Jiaxing 314001, China

At present, a single target optimization function is often used in channel design. While in order to meet the large capacity real-time transmission, it is necessary to consider the cumulative delay and channel capacity simultaneously. The multi-objective function of the target channel design was constructed, and discrete multi-objective particle swarm optimization algorithm(DMOPSO) was proposed to solve it. The discretization design of the population coding and updating was given. The simulation results show that the optimal channel set obtained by proposed spectrum handoff algorithm can take into account the real-time and high throughput of the network, while needing the low complexity.

multi-objective optimization, spectrum handoff, cumulative delay, channel capacity, particle swarm optimization

TN911

10.11959/j.issn.1000−0801.2018114

2017−10−09；

2018−02−27

赵知劲，Zhaozj03@hdu.edu.cn

“十二五”国防预研项目（No.41001010401）

12th Five-Year National Defense Advanced Research Program (No.41001010401)

张煜培（1995−），男，杭州电子科技大学硕士生，主要研究方向为认知无线电、频谱感知、频谱切换算法。