使用因素对滚动轮胎振动特性影响的有限元分析
2018-07-23张颖文王国林周海超
张颖文,王国林,周海超,杨 建
(江苏大学 汽车与交通工程学院,江苏 镇江 212013)
汽车噪声是交通噪声的主要来源之一。相关研究表明,乘用车和商用车速度分别高于40和75 km·h-1时,轮胎的振动噪声将成为车辆噪声的主要来源[1]。而结构振动噪声是载重子午线轮胎振动噪声的主要部分[2-3]。因此,研究轮胎振动特性及其影响因素对低噪声轮胎开发具有重要的意义。
轮胎振动噪声产生的机理是其结构的振动引起周围空气的扰动通过空气传播到人耳[4]。J.Lin等[5]采用结构模态分析方法分析了轮胎振动特性与辐射噪声之间的关系,结果表明,低阶模态对轮胎振动辐射噪声影响程度较大,并且峰值声压对应的频率往往在轮胎固有频率附近。Trong将轮胎简化为包含剪切应力和非线性效应的圆环,通过有限元分析验证了模型的准确性,并且用此模型分析了轮胎在非滚动和滚动状态下的特性,得到不同速度下轮胎的固有频率不同[6]。V.Q.Doan等[7]采用试验测试和有限元分析相结合的方法研究胎面振动加速度与轮胎噪声之间的关系,发现两者之间关系显著。包秀图等[8]提出一种轮胎在滚动时频域下的计算方法,将表面节点的振动速度转化为声学计算的频域边界条件,再利用声学边界元技术计算轮胎的低频振动噪声。蔡琼阳[9]研究了轮胎的振动特性,发现轮胎的振动模态影响其声辐射特性以及关系到车辆的多种性能。许志超等[10]采用试验方法研究了轮胎通过噪声与速度的关系,得到通过噪声声压级与速度对数呈线性关系的结果。国内外学者研究了轮胎结构部件的振动对噪声的影响,认为两者之间存在紧密的联系。因此,轮胎结构的振动特性可以成为振动噪声的主要评价指标,用于研究轮胎的振动噪声。
为了验证滚动轮胎有限元模拟分析方法的有效性,选取215/75R17.5载重子午线轮胎为研究对象,将试验和有限元仿真所得轮胎胎侧各测点时域下的振动速度进行傅里叶变换。在此基础上,研究轮胎使用因素对轮胎振动特性的影响,以期为解决轮胎在使用过程中遇到的噪声和振动问题提供指导。
1 滚动轮胎有限元分析
1.1 有限元模型的建立
利用文献[11]中的方法建立有限元模型,如图1所示。模型中轮辋和路面定义为解析刚体,橡胶部分采用CGAX3和CGAX4R单元模拟,钢丝帘线采用SFMGAX1和REBAR单元模拟。分析时,轮胎的载荷为10 000 N,充气压力为0.83 MPa。
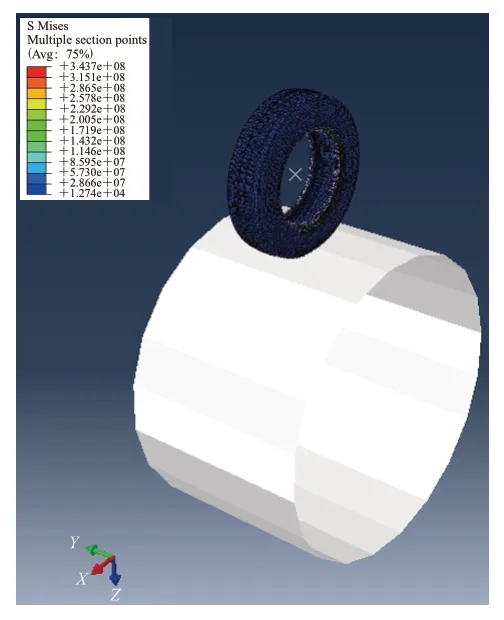
图1 轮胎三维有限元模型
橡胶的本构模型通过单轴拉伸试验获得,将测得的橡胶拉伸数据输入Abaqus中,利用其自带的Ogden,Neo-Hookean和Yeoh等橡胶本构模型分别进行拟合。以胎肩垫胶为例,其材料应力-应变曲线参照文献[12],在名义应变小于0.5时,Yeoh模型拟合的应力-应变曲线与试验结果吻合较好。因此,本研究选用Yeoh模型描述轮胎橡胶的力学特性。轮胎各部位的胶料参数由单轴拉伸试验数据拟合获得。
1.2 滚动轮胎数值仿真
利用Abaqus/Explicit模拟轮胎在30 km·h-1速度时的滚动过程。为分析滚动轮胎胎侧的振动特性,在胎侧上布置4个振动测试点,如图2所示。4个测点分布在与接触区域夹角为45°,135°,180°和315°的位置。测点1为接地后端,测点4为接地前端。有限元分析得到各测点时域下的振动速度如图3所示。
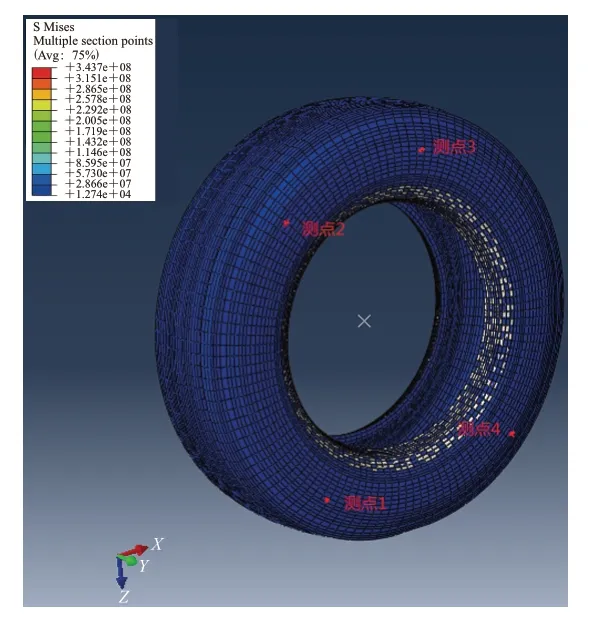
图2 有限元模型胎侧测点位置
从图3可以看出:测点与接地区域距离越近,振动速度幅值越大;接地后端的振动比接地前端剧烈。

图3 不同测点时域下的振动速度
2 滚动轮胎胎侧振动试验
2.1 轮胎振动响应试验
滚动轮胎胎侧振动特性试验是在转鼓试验台上进行的,如图4所示。试验时轮胎载荷为10 000 N,充气压力为0.83 MPa,测量速度为30 km·h-1。采用单点式多普勒激光测振仪测量轮胎胎侧的振动特性。为与有限元分析结果进行对比,振动测试点的布置与有限元分析一致。

图4 轮胎振动试验
试验时将多普勒激光测振仪固定在三脚架上,并将其通过数据采集器与电脑连接,如图5所示。三脚架距离被测轮胎大约50 cm,将激光束打到胎侧测点上,旋转调焦旋钮,当激光点最小、最亮时最佳,依次调节三脚架的位置分别对不同测点进行测量。

图5 多普勒激光测振仪
采样时间(ts)和频率(fs)分别设置为

式中,nF为频谱数,WB为带宽。测试时对每个测点多次测量,结果取平均值。为了方便与有限元分析结果进行对比,对试验数据进行滤波。滤波时采用Matlab中等波纹低通滤波器Firpm函数,其通过频率为20 Hz,截止频率为500 Hz。图6示出了随机测点滤波前后的振动速度对比结果。
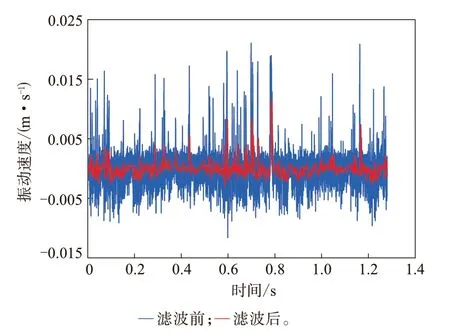
图6 测点滤波前后振动速度对比
从图6可以看出,滤波前后曲线的波动趋势大致相同,峰值分布也类似。
2.2 结果与分析
图7和8分别示出不同测点振动速度以及接地前后端测点振动速度的对比情况。
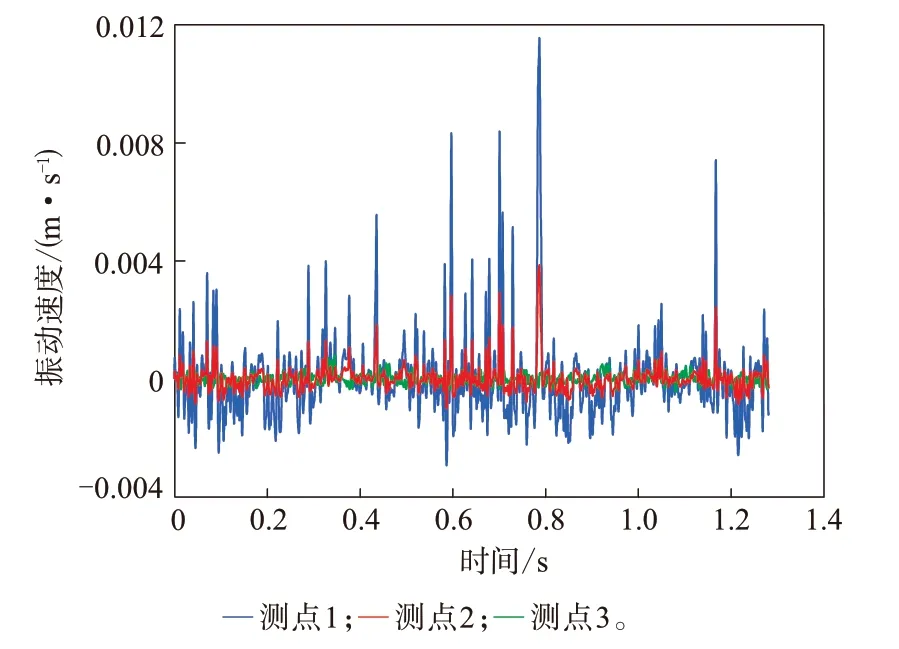
图7 不同测点的振动速度
从图7可以看出,在相同速度下,测点1,2和3的振动速度幅值呈递减的趋势,这说明越靠近接地区域,胎侧的振动越剧烈。这与文献[13]中靠近接地区域声能量分布高表明该区域振动剧烈的结论相一致。从图8可以看出,轮胎接地后端的振动响应大于接地前端,接地前端振动速度的峰值明显小于接地后端。文献[14]采用室内转鼓试验测试载重子午线轮胎近场噪声,结果表明,轮胎接地后端的振动噪声声压级大于轮胎接地前端的振动噪声声压级,而振动噪声声压级与振动剧烈程度呈正相关性,这一结果与试验结果相一致。
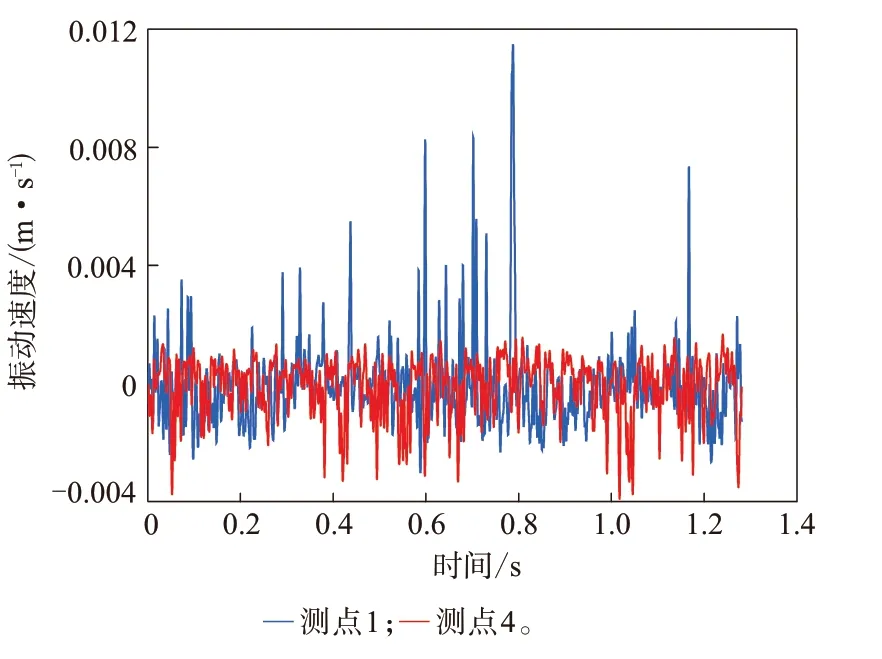
图8 接地前后端测点的振动速度
不同测点时域下实测结果与有限元仿真结果的对比情况如图9所示。
从图9可以看出,3个测点时域下的振动速度曲线变化趋势一致。为了更好地将实测值与仿真值进行比较,将时域下的信号进行离散傅里叶变换,得到频域下的振动速度曲线,结果如图10所示。可以看出,胎侧测点试验和仿真得到的振动速度在频域下的分布具有良好的一致性,证明所建滚动有限元模型有效。
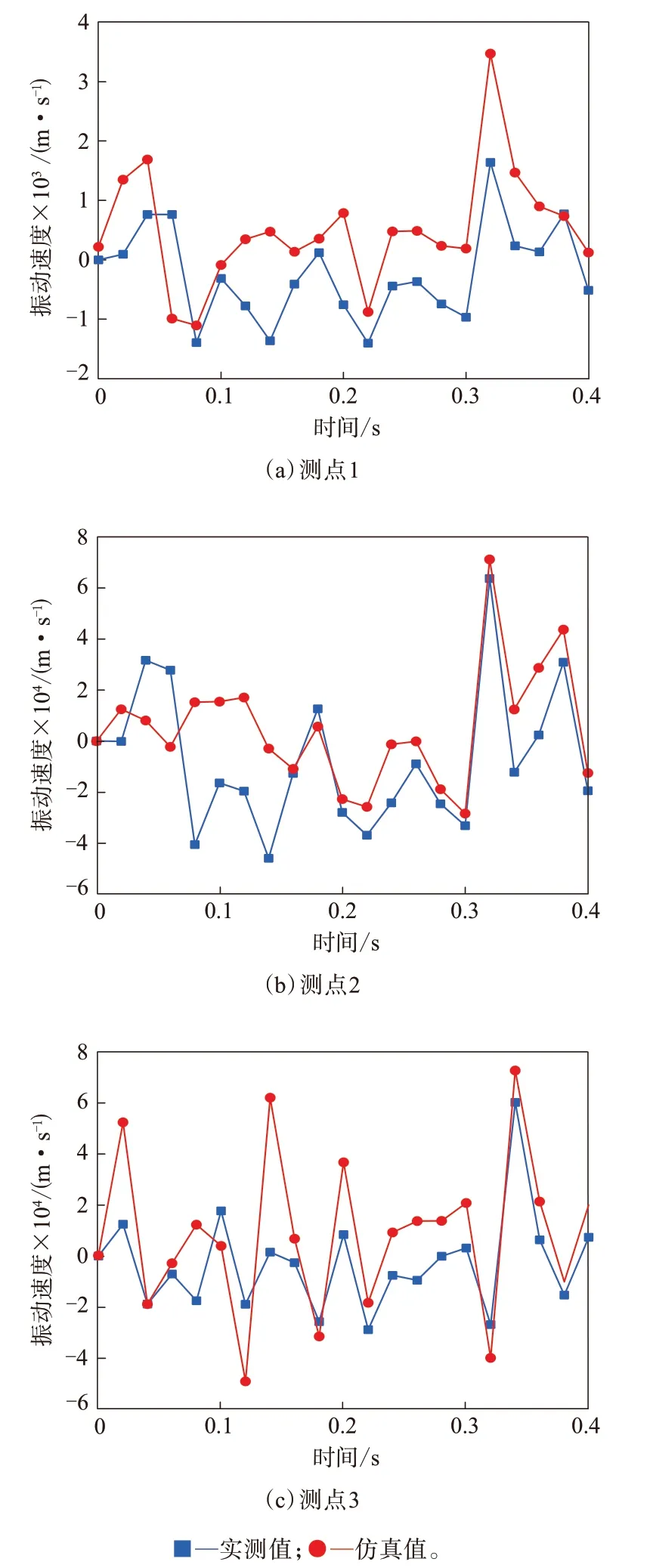
图9 不同测点时域下振动速度实测值与仿真值对比

图10 离散傅里叶变换后不同测点频域下振动速度实测值与仿真值对比
3 使用因素对轮胎振动特性的影响
为分析轮胎使用因素对振动特性的影响,采用单一变量法,研究速度、充气压力和载荷对胎面和胎侧振动特性的影响规律。
3.1 滚动速度
在轮胎充气压力和载荷均为额定值的情况下,研究不同速度下胎侧和胎面圆周上振动速度分布,结果如图11所示。

图11 不同速度下轮胎圆周上振动速度分布
图11中坐标轴原点代表轮胎上顶点位置,沿着X轴正方向为轮胎接地前端方向圆周区域,负方向为轮胎接地后端方向圆周区域,图形两边端点即为轮胎的接地中心点。从图11(a)可以看出:胎侧圆周振动速度分布近似关于原点对称;随着速度的增大,胎侧的振动速度也随之增大,在±169°的圆周上出现峰值,在-150°~150°范围内振动幅值较小,且趋于平缓。从图11(b)可以看出,随着轮胎滚动速度增大,胎面部分的振动速度也随之增大,不同速度下胎面振动速度总体波动较大,在±153°圆周点上出现峰值。胎侧、胎面接地后端的振动速度均大于接地前端的振动速度。
3.2 充气压力
在轮胎滚动速度一定(70 km·h-1)和载荷为额定负荷的情况下,研究不同充气压力下胎侧和胎面圆周上振动速度分布,结果如图12所示。
从图12(a)可以看出:胎侧圆周振动速度分布关于原点对称;随着充气压力的增大,胎侧的振动速度也随之增大,在±169°的圆周上出现峰值,在-150°~150°范围内振动幅值较小,且趋于平缓。从图12(b)可以看出:0.9倍额定充气压力和额定充气压力下胎面的振动速度大致相等,1.2倍额定充气压力下胎面振动速度最大;不同充气压力下胎面振动速度总体波动较大,在±153°圆周点上出现峰值。胎侧、胎面接地后端的振动速度均大于接地前端的振动速度。

图12 不同充气压力下轮胎圆周上振动速度分布
3.3 载荷
在轮胎滚动速度一定(70 km·h-1)和额定充气压力的情况下,研究不同载荷下胎侧和胎面圆周上振动速度分布,结果如图13所示。
从图13(a)可以看出:胎侧圆周振动速度分布近似关于原点对称;随着载荷的增大,胎侧振动速度变化量较小,在±169°的圆周上出现峰值,在-150°~150°范围内振动幅值较小,且趋于平缓。从图13(b)可以看出,胎面振动速度随着载荷的增大变化较小,但波动较大。胎侧和胎面接地后端的振动速度均大于接地前端的振动速度。
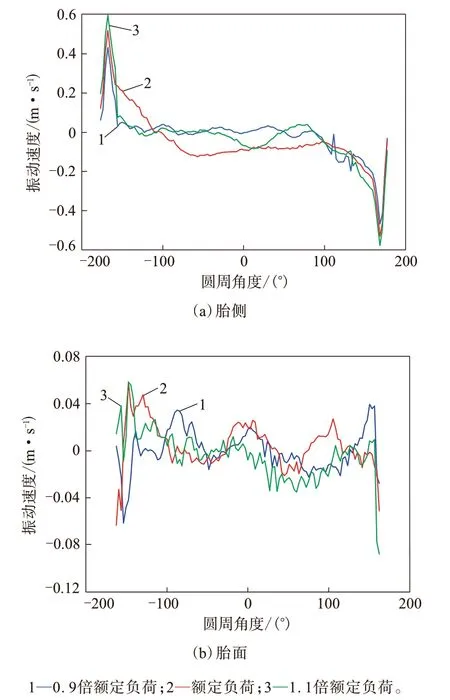
图13 不同载荷下轮胎圆周上振动速度分布
4 结论
(1)轮胎滚动有限元模型胎侧测点频域下的振动速度与轮胎转鼓试验时胎侧的振动速度具有良好的一致性,验证了轮胎滚动有限元模型的准确性。
(2)胎面的振动速度分布关于轮胎顶点对称,靠近接地区域振动速度幅值最大,接地后端振动速度大于接地前端;随着速度和充气压力的增大,胎面和胎侧的振动速度随之增大,载荷对胎面和胎侧振动速度的影响较小。
