橡胶等双轴拉伸十字形试样的设计与有限元分析

2018-07-23周华森杨晓翔

橡胶工业 2018年10期

周华森，杨晓翔，2*

（1.福州大学机械工程及自动化学院，福建福州 350116；2.泉州师范学院，福建泉州 362000）

为了精确地表征橡胶材料的力学性能，需要进行多种准静态力学试验，包括单轴拉伸、等双轴拉伸和平面拉伸试验等[1-2]。相比于单轴拉伸试验，等双轴拉伸试验没有相应的标准测试方法，研究人员采用了多种不同的试验方法[3-7]来获得橡胶材料的等双轴应力状态，其中通过十字形试样来进行平面双轴拉伸试验是目前研究的热点。该方法通过双轴拉伸试验机直接对十字形试样完成复杂加载，使试样的中心测试区呈现等双轴应力状态，最终得到其名义应力-拉伸比关系曲线。

十字形试样的设计与优化是双轴拉伸试验的关键环节，需针对不同的材料设计不同形状的十字形试样。Y.Hanabusa等[8]基于T.Kuwabara等[9]设计了臂上开缝型十字金属试样，采用有限元方法分析了试样的厚度、缝的数量、长度、宽度和倒角半径对中心测试区应力分布均匀性的影响，并结合双轴拉伸试验验证了有限元分析结果的可靠性。蔡登安等[10]基于双轴拉伸载荷下复合材料十字形试样的设计特点，对比分析了不同几何形状的十字形试样在不同厚度比和载荷比条件下中心测试区应力集中系数和承力系数的变化规律，并进行了不同载荷比的双轴拉伸试验验证。A.Makris等[11]通过有限元参数化建模与数值优化方法相结合对复合材料十字形试样的几何形状进行优化设计，优化后的试样中心区应变场均匀性得到明显提高。

本工作针对橡胶材料的等双轴拉伸试验，设计了4种不同形状的十字形试样，并通过Abaqus有限元软件进行仿真分析和比较，为橡胶等双轴拉伸试验提供参考。

1 超弹性本构理论

1.1 基础理论

橡胶是一种超弹性材料，当经历大变形时其应力-应变关系呈现出强烈的非线性特征。基于连续介质力学理论，一般认为橡胶材料是各向同性不可压缩的弹性体，它的本构关系可以通过3个主拉伸比的应变能密度函数（W）来表示[12]：

式中，λ1，λ2，λ3为3个方向的拉伸比。基于不可压缩条件（λ1λ2λ3＝1），只有两个方向上的主拉伸比是相互独立的，则应变能密度函数又可表示为

R.W.Ogden[13]给出了与主拉伸比相对应的Cauchy主应力（σ）的表达式：

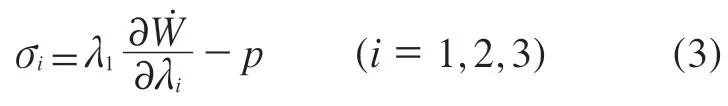
式中，p为静水压力，根据上式两两相减可消去，即

对于平面内的拉伸试验，垂直于平面方向的应力为0，即σ3＝0，代入式（4）和（5）可得：

根据名义应力Si＝σi/λi可得到名义应力与拉伸比的关系式为

对于理想状态下的等双轴拉伸试验

则式（2）的应变能密度函数又可以表示为

于是等双轴拉伸状态下名义应力（S）与拉伸比的关系式为

1.2 Ogden模型

Ogden模型是目前工程上应用最为广泛的超弹性本构模型之一，其应变能密度函数形式为[13]：

式中，μi和αi为材料常数，阶数N可根据实际情况调整。可见Ogden模型具有很大的灵活性，目前使用最多的是Ogden三阶模型。试验的种类越多，使用Ogden模型拟合试验数据越准确，通过式（10）即可得到Ogden模型在等双轴载荷作用下的名义应力-主拉伸比关系式为

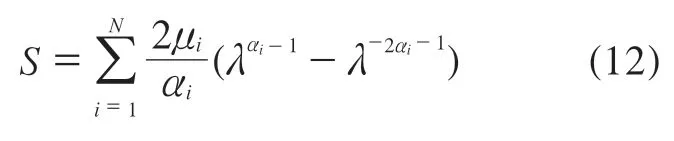
2 有限元模型的建立

2.1 等双轴拉伸试验方法

在实际的等双轴拉伸试验中，通过4个相同的夹具夹持住十字形试样每个臂的末端，设置相同的拉伸速率来实现对4个臂的同步加载，在试样的中心区域可以呈现出近似的等双轴变形状态，如图1所示。中心区域内的应力和应变的分布是相对均匀的。为了得到橡胶材料的名义应变数据，通常在试样表面的中心标记出一个正方形区域作为中心测试区，采用非接触式测量方法即可获得该区域的拉伸比数据[14]，计算公式如下：

图1 十字形试样等双轴拉伸示意

式中，L为拉伸变形后的中心测试区的长度，L0为其变形前的初始长度。在不考虑试验误差的情况下，由于受到试样几何形状的影响，理论上只有中心点能呈现理想的等双轴变形状态。因此，中心测试区的长度越小，测量的结果越准确，但实际很难测量小范围内的应变。对于不同几何形状的十字形试样，在进行等双轴拉伸试验时其中心测试区的应力场及其分布情况是不一样的。为了保证测量结果的准确性和有效性，要求所设计的橡胶十字形试样满足如下要求：（1）中心测试区尽可能接近等双轴变形状态；（2）中心测试区的应力和应变分布是均匀的；（3）中心测试区应能产生较大的应变。

2.2 有限元建模

设计了4种不同形状和尺寸的十字形试样，如图2所示，试样的厚度和夹持区长度分别为2和10 mm。A型和B型试样为最常规的十字形试样，与A型试样相比，B型试样减小了十字臂的宽度，增大了倒角半径。C型试样根据J.J.Hu等[15]的研究设计，而D型试样是基于单轴拉伸所用的哑铃形试样设计的。

图2 4种十字形试样的设计

相比于试验，有限元分析方法可以确定试样中心测试区上每一点的应力和应变状态，这为试样的设计提供了良好的帮助。本工作采用有限元软件Abaqus模拟橡胶十字形试样的等双轴拉伸试验。十字形试样的几何形状比较简单，直接使用Part模块中的相关工具即可完成。由于模型的对称性，为了节省计算时间，在有限元建模时只需建立1/4的试样模型。试验时试样夹持区的刚度远大于其他部位，因此建模时不考虑这部分区域。橡胶材料模型选用不可压缩的Ogden超弹性本构模型，其材料参数（N＝3）如下[5]：α12.033 6 MPa，μ1－ 0.990 0，α2－ 2.573 1 MPa，μ2－ 0.774 9，α31.620 0 MPa，μ31.691 0。

Abaqus/Standard中每一种实体单元都有其对应的杂交单元[16]，可用于分析不可压缩材料，本工作采用八节点线性六面体杂交单元C3D8RH划分十字形试样。以A型试样为例，在模型的左部和底部施加对称边界条件，在两个十字臂末端施加25 mm的均匀线性位移载荷，同时设置中心测试区长度L0＝10 mm，即OA＝AB＝5 mm，建立的有限元模型如图3所示。

图3 A型试样有限元模型

3 结果与讨论

根据建立的有限元模型，对4种试样进行等双轴拉伸试验模拟，并根据中心测试区的应力和应变分布状况对其进行评价。

3.1 名义应力-拉伸比关系曲线

由于模型和载荷的对称性，沿X轴方向和Y轴方向的应力和应变分布的规律是一致的。根据式（13），在Abaqus中提取AB边各节点沿X轴方向的真实应力和名义应变，求得其平均值并经过换算即可得到各试样的名义应力-拉伸比关系曲线，并与采用Ogden本构模型的理论曲线进行对比，如图4所示。由图4可以看出，在标记位置相同的情况下，通过仿真分析得到的A型试样名义应力-拉伸比关系曲线与理论曲线几乎完全吻合，其次是B型试样，说明中心测试区的选取位置是合适的。而C型试样随着拉伸比的逐渐增大，其曲线越来越偏离理论曲线，D型试样则只有在拉伸比为1.7左右时与理论曲线较接近。

图4 有限元模拟曲线与理论曲线对比

3.2 应力场分析

4种试样变形后的von Mises应力云图如图5所示。从图5可以看出，各个试样在加载端应力不均匀且均出现了不同程度的应力集中现象：A型、C型和D型试样在倒角处发生应力集中，而B型试样在拉伸臂的尾端出现应力集中，其中D型试样的应力集中范围最广。对于A型和B型试样，沿着中心点往拉伸臂的边缘应力逐渐增大，而C型和D型试样的应力则是先增大后减小，在较大载荷作用下容易引起拉伸臂中部破裂。相比于其他试样，A型试样的中心区域产生了较大范围的均匀应力场，且其整体的应力分布也最为均匀，而D型试样的应力分布均匀性最差。

图5 von Mises应力云图

3.3 应变场分析

应变场的分布规律与应力场基本一致，由于应变测量技术的局限性，为了得到理想的十字形试样，需要对各个试样的中心试验区的应变场进行评价。由于模型的对称性，只需考虑试样沿X方向的应变分布状态。在Abaqus中设置路径OA，提取路径上各节点沿X方向和Y方向的名义应变εX和εY，如图6所示。由图6可以看出，各个试样中心测试区的名义应变沿X方向和Y方向的变化趋势是相反的，εX随着距中心点距离的增大而逐渐增大，而εY则逐渐减小。其中，A型试样在中心测试区内沿X方向和Y方向的名义应变较大且变化幅度最小。

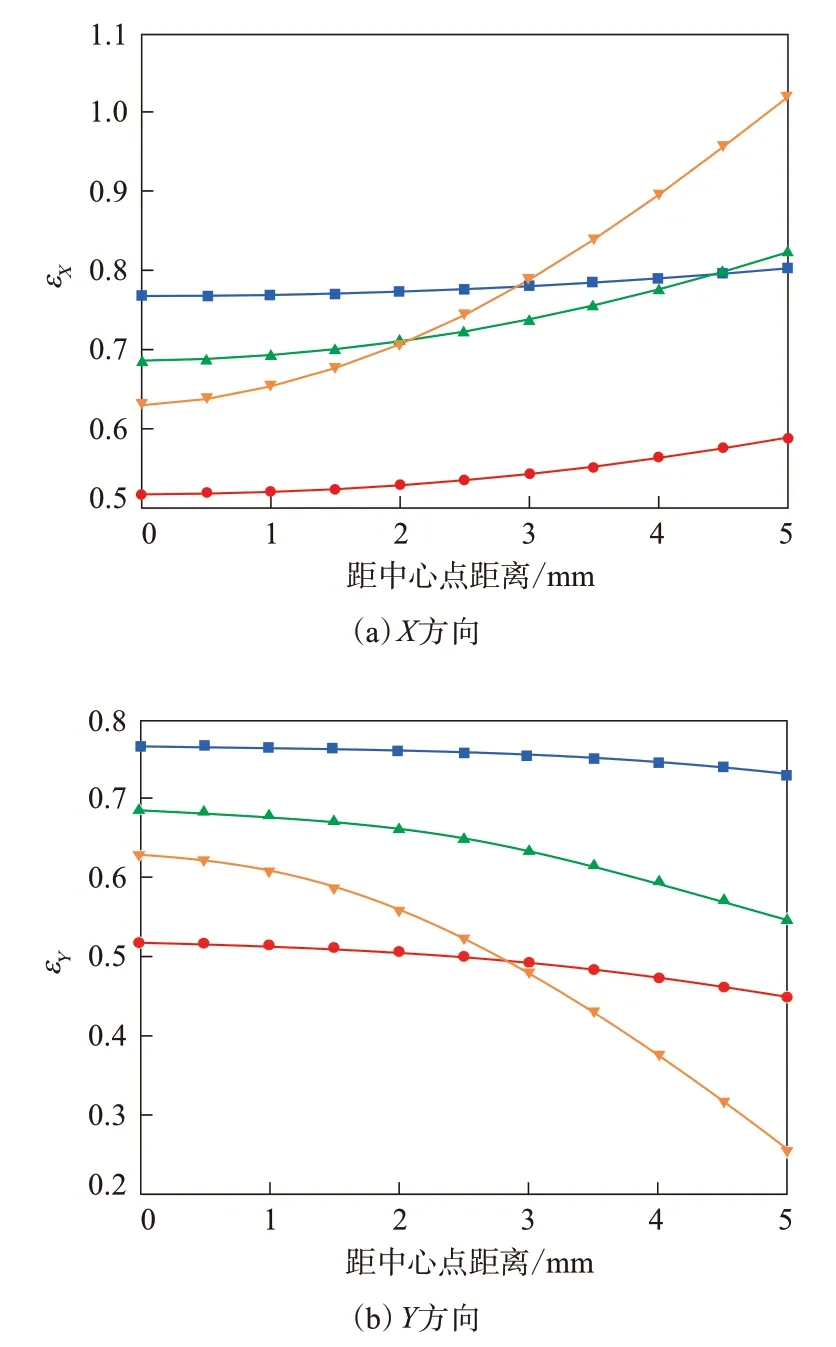
图6 沿路径O A的名义应变变化

根据设计要求，为了更直观地评价各个十字形试样的优劣，定义中心测试区的等双轴变形状态系数α和均匀性系数β分别为

式中，ε X0为中心点O沿X方向的名义应变。当α和β的值越接近于0，则说明试样的中心测试区接近理想的均匀等双轴变形状态。同样以路径OA为研究对象，计算该路径上各节点的α和β值，如图7和8所示。由图7和8可见，α和β均随着距中心点距离的增大而增大。其中，A型试样中心测试区内α和β均小于其他试样，且接近于0，说明A型试样最符合设计要求。同时，在测量条件允许的情况下，可以通过减小测试区域的大小，使其更接近理想的等双轴变形状态。