坦克稳态行驶动力性燃油经济性参数计算模型

王普凯， 韩立军， 康 琦， 董 意， 何盼攀

(陆军装甲兵学院车辆工程系， 北京 100072)

坦克集火力、机动和防护3大性能于一体,是现代战争中地面突击作战的主战装备。动力性和燃油经济性是坦克性能的重要指标，其对坦克机动性有重要影响，其中：动力性强，则坦克的战役战术机动性能好；经济性好，则有利于坦克长距离机动作战。为此，论证设计坦克时，必须把其动力性燃油经济性作为重要的参数来考虑。

研究坦克的动力性燃油经济性参数，可以采取实验[1]和计算[2-3]2种方法。然而，实验成本高，且无法详细研究发动机工况、驾驶员状态和环境因素对坦克动力性燃油经济性参数的影响；计算成本低，但目前常用的方法是将发动机特性作为已知条件计算[2-3],不能体现坦克动力性经济性参数与发动机工作的真实关系。

为此，笔者建立一种坦克稳态行驶动力性燃油经济性参数计算模型,以方便坦克动力性燃油经济性参数的计算。

1 计算模型

将柴油机工作模型和坦克行驶模型相结合，建立坦克稳态行驶动力性燃油经济性参数计算模型。

1.1 柴油机工作模型

图1为某型坦克所用的废气涡轮增压中冷柴油机的结构示意图。图2为利用GT-POWER建立的柴油机工作模型，利用该模型可计算得到不同工况下柴油机的动力性燃油经济性参数。

1.1.1 缸内热力过程模型

采用零维模型计算缸内热力过程[4]。由缸内热力系统能量守恒，可得缸内温度变化微分方程为

(1)

由缸内热力系统质量守恒，可得缸内质量变化微分方程为

(2)

理想气体状态方程为

pV=mRT。

(3)

式中：φ为曲轴转角；m为缸内气体质量；p、V、T分别为缸内气体的压力、容积和温度；Qb、Qw为与气体的交换热量；λ为过量空气系数；cv为气体定容比热；U为缸内单位质量气体对应的内能；H为缸内单位质量气体对应的焓；H2为流入气缸单位质量气体对应的焓；mb为缸内燃油质量；me为流经进气门的气体质量；ma为流经排气门的气体质量；R为理想气体常数。

1.1.2 进/排气管路气体流动模型

进/排气管路内的气体做有摩擦、有传热的一维非定常流动，采用“有限容积法”计算其热力参数及流动状态[5-6]。进/排气管路内的容积划分如图3所示。

描述进/排气系统内部流动的连续方程、能量方程和动量方程如下：

连续方程为

(4)

能量方程为

(5)

动量方程为

(6)

1.2 坦克行驶模型

图4为利用GT-DRIVE建立的坦克行驶模型。该模型考虑了大气温度、发动机转速、变速箱排挡、路面条件和弯转半径等因素的影响。

坦克直线行驶的总阻力Rr主要由纵向坡道阻力Rθ、空气阻力Ra和地面阻力Rf三部分组成[3]，即

Rr=Ra+Rθ+Rf。

(7)

典型路面对应的地面阻力系数如表1所示[7]。

表1 典型路面对应的地面阻力系数

坦克直线行驶总阻力矩为

Mr=ωRr；

(8)

若坦克匀速转向行驶，则会在Mr的基础上额外产生转向阻力矩Mμ[8]，即

(9)

式中：L为履带接地段长度；

为横向阻力和法向负荷比例系数[4]，其中μmax根据路面类型选定[4]，k为转向半径与履带中心距之比。

1.3 单缸循环供油量计算过程

将基于GT-POWER的柴油机工作过程模型和基于GT-DRIVE的坦克行驶模型相结合，建立坦克稳态行驶动力性燃油经济性参数计算模型，实现坦克动力传动的自动耦合计算。计算时，在已知柴油机转速、变速箱排挡、路面和大气环境参数的情况下，还需要输入合适的单缸循环供油量，以使柴油机的动力输出与所受载荷相等，即保证坦克稳态行驶。由此可见，单缸循环供油量的选择是实现坦克稳态行驶的关键，可采用迭代计算的方法得到，具体过程为：

1) 输入计算所需的已知条件和参数，包括柴油机结构尺寸数据、气体流动和摩擦损失试验数据，坦克车重、传动装置传动比、传动效率和主动轮半径，地面阻力系数、路面弯转半径、大气温度、柴油机转速和变速箱排挡。

2) 假定柴油机单缸循环供油量。

3) 根据柴油机工作过程模型计算柴油机有效扭矩。

4) 根据坦克行驶模型计算坦克行驶阻力。

5) 根据坦克行驶阻力、传动装置传动比和传动效率反推柴油机负荷。

6) 根据柴油机有效扭矩和负荷计算柴油机转速变化率。

7) 根据柴油机转速变化率、传动装置传动比计算车速变化率。

8) 判断车速变化率是否小于0.01 km/(h·s)，如果是，结束供油量迭代计算，输出计算结果；否则，调整单缸循环供油量，然后返回步骤3)。

1.4 柴油机工作过程模型精度验证

基于所调研的柴油机台架试验数据，验证所建立柴油机工作过程模型的精度。取大气压力为89.9 kPa，大气温度为28 ℃，油门开度为100%，柴油机转速分别为2 000、1 800、1 600、1 400 r/min，验证结果如表2所示。可以看出：柴油机有效功率、有效比油耗、压气机压比和压气机流量的最大相对计算误差为9.95%，这表明所建立的柴油机工作过程模型精度较高。

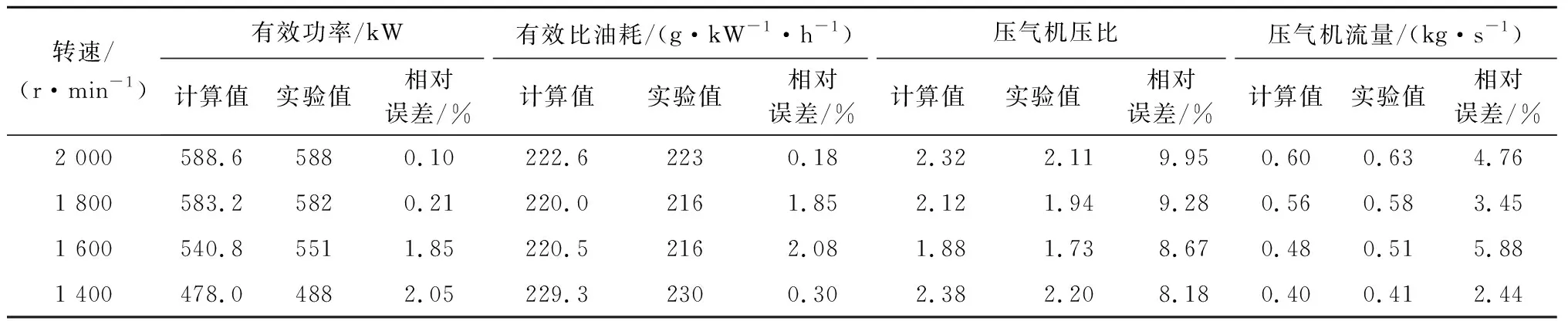
表2 柴油机工作过程模型精度验证结果

2 计算实例

取大气压力为101.3 kPa、大气温度为25 ℃，以某中型坦克为研究对象，计算柴油机有效功率、有效扭矩、有效比油耗以及坦克百公里油耗等参数随柴油机转速、变速箱排挡、地面阻力系数和路面弯转半径等因素的变化。其中，有效功率、有效扭矩、有效比油耗可由GT-POWER软件直接输出。对于采用四行程柴油机的坦克，其稳态行驶百公里油耗的计算公式为

(10)

式中：Be为百公里油耗(L/(100 km))；ne为柴油机转速(r/min)；ic为柴油机气缸数目；be为柴油机单缸循环供油量(mg)；u为坦克行驶速度(km/h)；rz为主动轮半径(m)；kz为总传动比；ρf为柴油密度，取值为860 kg/m3。

2.1 计算结果

2.1.1 柴油机转速

取变速箱排挡为4，路面为水泥路(地面阻力系数为0.044 5)。迭代计算得到坦克稳态直线行驶时,柴油机的单缸循环供油量、有效功率、有效扭矩、有效比油耗和坦克百公里油耗随柴油机转速的变化曲线，如图5所示。可以看出：柴油机的单缸循环供油量、有效功率、有效扭矩、有效比油耗和坦克百公里油耗均随柴油机转速的升高而增大。

2.1.2 变速箱排挡

取柴油机转速为2 000 r/min，路面为水泥路(地面阻力系数为0.044 5)。经迭代计算，得到坦克稳态直线行驶时柴油机的单缸循环供油量、有效功率、有效扭矩、有效比油耗和坦克百公里油耗随变速箱排挡的变化曲线，如图6所示。可以看出：柴油机的单缸循环供油量、有效功率、有效扭矩随变速箱排挡的增加而增大，有效比油耗和坦克百公里油耗随变速箱排挡的增加而降低。

2.1.3 地面阻力系数

取柴油机转速为2 000 r/min，变速箱排挡为1。经迭代计算，得到坦克稳态直线行驶时柴油机的单缸循环供油量、有效功率、有效扭矩、有效比油耗和坦克百公里油耗随地面阻力系数的变化曲线，如图7所示。可以看出：柴油机的单缸循环供油量、有效功率、有效扭矩和坦克百公里油耗均随地面阻力系数的增大而增大，而有效比油耗随地面阻力系数的增大而降低。

2.1.4 路面弯转半径

取柴油机转速为2 000 r/min，变速箱排挡为3，路面为水泥路(地面阻力系数为0.044 5)。经迭代计算，得到坦克稳态转向行驶时柴油机的单缸循环供油量、有效功率、有效扭矩、有效比油耗和坦克百公里油耗随路面弯转半径的变化曲线，如图8所示。可以看出：柴油机单缸循环供油量、有效功率、有效扭矩和坦克百公里油耗均随路面弯转半径的增大而减小，而有效比油耗随路面弯转半径的增大而升高。

2.2 结果分析

随着柴油机转速、变速箱排挡和地面阻力系数的增加，坦克行驶总阻力增大，需要的柴油机单缸循环供油量增加，使得柴油机有效功率和有效扭矩增大；随着路面弯转半径的增大，坦克行驶总阻力减小，需要的柴油机单缸循环供油量减少，使得柴油机有效功率和有效扭矩减小。

有效比油耗正比于柴油机单缸循环供油量和有效扭矩之比。随着柴油机转速的升高，车速增加，由于只是空气阻力增加，因此总阻力增加不明显，使得有效扭矩增大不多，而单缸循环供油量则增加明显，因此有效比油耗升高；随着变速箱排挡的升高，车速增加，使曲轴的阻力矩增幅明显，即有效扭矩增幅明显，且增速大于单缸循环供油量，因此有效比油耗降低；随着地面阻力系数的增大，坦克总阻力增加明显，但有效扭矩比单缸循环供油量增速快，因此有效比油耗降低；随着路面弯转半径的增加，坦克总阻力减小明显，使得有效扭矩比单缸循环供油量减速要快，因此有效比油耗增加。

由式(10)可知：坦克百公里油耗正比于柴油机单缸循环供油量和总传动比。随着柴油机转速的升高，单缸循环供油量增加，因此坦克百公里油耗升高；随着变速箱排挡的升高，单缸循环供油量增加而总传动比降低，但总传动比降速更快，因此坦克百公里油耗降低；随着地面阻力系数的增大，单缸循环供油量增加，因此坦克百公里油耗升高；随着路面弯转半径的增大，单缸循环供油量减小，因此坦克百公里油耗降低。

3 结论

基于GT-POWER的柴油机工作过程模型和GT-DRIVE的坦克行驶模型，笔者建立了坦克稳态行驶动力性燃油经济性参数计算模型,通过台架试验数据验证了模型精度，并通过案例进行了计算分析，结果表明：该模型精度较高，能够实现柴油机工作和坦克行驶的耦合计算，为坦克稳态行驶动力性燃油经济性参数的计算提供了一种系统、便捷的方法。下一步，将研究坦克动态行驶动力性燃油经济性参数计算模型的建立方法。