基于信息熵的师级装备保障机构编配能力评价

王 帅， 李 婷， 崔 静

(陆军工程大学石家庄校区信息工程系， 河北 石家庄 050003)

开展信息化条件下装备保障机构编配模式能力评估研究，是提高装备保障效率和指挥质量，确保装备保障指挥模式成功转型的重要保证[1]。苏凡囤等[2]对工程装备维修机构能力评估进行了研究，王琦等[3]对弹药维修机构维修能力评估进行了研究，但有关装备部门的机构编配能力研究还较少。笔者以师级部队为研究背景，以装备保障机构编配模式为研究对象，对装备保障机构层级进行了划分，并将实体及其相互之间的关系抽象为节点与边，实现了装备保障机构编配模式的数学描述，应用信息熵理论建立了装备保障机构编配模式能力评价模型，对不同编配模式下的装备保障机构的保障能力进行了评估，为装备保障机构编配提供了量化依据。

1 装备保障机构编配模式及其数学描述

1.1 装备保障机构编配模式

目前，装备保障机构的编配模式主要有2种：按照装备专业方式编配(模式1)和按照装备保障行动方式编配(模式2)。当按照模式1进行编配时，师级装备保障机构可划分为战勤科、装甲科、军械科、工化科、轮式车辆科和直政科等，这是传统部队的编配模式。当按照模式2进行编配时，师级装备保障机构则划分为战勤科、管理科、储供科和直政科等。

模式1的优点是各科室之间分工明确，不同类型装备的业务由对口的装备科室来处理，各科室之间协调起来也很方便，相互之间和冲突和矛盾；缺点是各科室较为独立，科室之间沟通不多。

模式2的优点是各科室按职能分工，装备保障关系顺畅，便于提高相关业务的熟练程度，若部队列装新型武器装备，则不需要成立新的科室；缺点是各科室间职责界线划分困难，业务易重叠、冲突。

1.2 编配模式的数学描述

为简化模型，首先，假设模式1、2中都编配了战勤科和直政科，并视二者作用等同，因此建模时可同时略去，以降低保障机构节点的关联度，有助于简化计算。其次，现有装备保障机构指挥的装备保障分队具有2种编配形式：按装备种类编配和按装备构成编配，前者可编配各种类型的装备保障分队，如军械、装甲、工化、轮式车辆等分队，后者可编配装备各组成模块的保障分队，如履带(轮式)底盘、上装、特装等分队。本文中，装备保障分队的编配形式采取按装备种类来编配，由此得出装备保障机构编配模式的组织结构。

当按模式1编配时，师装备保障机构各科室通过装备管理、装备维修、装备储供和信息管理职能来指挥各装备保障分队，此时装备保障机构的组织结构如图1所示。将各科室抽象为节点，各科室之间的联系抽象为边，则其组织结构抽象图如图2所示。

当按模式2编配时，师装备保障机构各科室直接指挥各个装备保障分队，此时装备保障机构的组织结构如图3所示，其抽象图如图4所示。

2 编配模式能力评价模型

笔者采用信息熵理论[4-5]，以装备保障机构的组织结构中各种信息的流通和交互情况为研究重点，采用时效性来衡量指挥信息获取和传递的不确定性，即流通时效维度的有序度,采用质量性来衡量指挥信息在传递过程中出错概率，即信息准确维度的有序度，然后将二者综合起来衡量装备保障机构的整体能力。引入信息熵来评价装备保障机构的整体能力，其时效性和质量性分别采用装备保障机构的时效熵和质量熵来度量。

2.1 装备保障机构的时效性评价模型

设Lij为节点i、j(i≠j,i,j=1,2,…，N,N为装备保障机构中节点的总数)间的最小距离，且为数值，不具备方向性，则

(1)

式中：n为节点i、j间的中转次数。

(2)

为组织结构中关联节点i、j间实现转移的概率。则自上而下任意2个节点间的时效熵

(3)

装备保障组织结构的总时效熵

(4)

Ht越低，表明该组织结构的有序化程度越高，结构越合理。

根据文献[4]，定义组织结构的总时效熵达到最大时为该组织结构的最大时效熵，即

(5)

式中：Ω为装备保障机构中所有可能的编配模式集合。

系统时效熵与最大时效熵的比值可反映组织结构的无序程度，因此定义时效性

(6)

用以反映组织结构的有序度。在实际应用中，R越大，说明该组织结构越合理。

2.2 装备保障机构的质量性评价模型

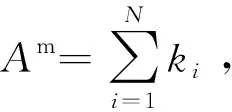
(7)

其可从本质上反映某一节点的出错概率。

与时效熵类似，分别定义装备保障机结构的总质量熵与最大质量熵如下:

总质量熵为

(8)

Hm越低，表明该组织结构的有序化程度越高，结构越合理。

最大质量熵为

(9)

系统质量熵与最大质量熵的比值也可反映组织结构的无序程度，因此定义质量性

(10)

用以反映组织结构的有序度。在实际应用中，Q越大，说明该组织结构的有序度越高，结构越合理。

2.3 装备保障机构的整体能力评价

装备保障机构的整体能力(E)由时效性和质量性综合决定，则E=ω1R+ω2Q，E越大，表明组织结构的有序度越高，整体保障能力越强。其中ω1、ω2(ω1+ω2=1)分别表示系统内部信息流通的时效性和质量性对系统结构有序性的影响程度：若时效性的影响更大，则ω1的取值就越大；若质量性的影响更大，则ω2的取值就越大[6]。

3 实例分析

当装备保障机构采用不同的编配模式时，其组织结构亦不同，对系统内部信息流通的时效性和质量性要求也不同。本文中，设时效性和质量性对装备保障机构编配模式整体能力的影响大致相当，即E=(R+Q)/2。

3.1 2种编配模式下装备保障机构的时效性

以模式1为例，由图2可知，其组织结构中关联长度为1的节点有36个，对应的节点序号为：1-2、1-3、1-4、1-5、2-6、2-7、2-8、2-9、3-10、3-11、3-12、3-13、4-14、4-15、4-16、4-17、5-18、5-19、5-20、5-21、6-22、7-22、8-22、9-22、10-23、11-23、12-23、13-23、14-24、15-24、16-24、17-24、18-25、19-25、20-25、21-25，时效关联总长度为36。关联长度为2的节点有32个，对应的节点序号为：1-2-6、1-2-7、1-2-8、1-2-9、1-3-10、1-3-11、1-3-12、1-3-13、1-4-14、1-4-15、1-4-16、1-4-17、1-5-18、1-5-19、1-5-20、1-5-21、2-6-22、2-7-22、2-8-22、2-9-22、3-10-23、3-11-23、3-12-23、3-13-23、4-14-24、4-15-24、4-16-24、4-17-24、5-18-25、5-19-25、5-20-25、5-21-25，时效关联总长度为64。关联长度为3的节点有16个，对应的节点序号为：1-2-6-22、1-2-7-22、1-2-8-22、1-2-9-22、1-3-10-23、1-3-11-23、1-3-12-23、1-3-13-23、1-4-14-24、1-4-15-24、1-4-16-24、1-4-17-24、1-5-18-25、1-5-19-25、1-5-20-25、1-5-21-25，时效关联总长度为48。因此，模式1下装备保障机构的时效关联总长度At=36+64+48=148，关联长度为1的pij=1/148；关联长度为2的pij=2/148；关联长度为3的pij=3/148。

3.2 2种编配模式下装备保障机构的质量性

在模式1下，不存在关联数为1和3的节点；关联数为2的节点有16个，对应的节点序号为6、7、8、9、10、11、12、13、14、15、16、17、18、19、20、21，质量联系总数=32；关联数为4的节点有5个，对应的节点序号为1、22、23、24、25，质量联系总数=20;关联数为5的节点有4个，对应的节点序号为2、3、4、5，质量联系总数=20。因此，模式1下装备保障机构的质量关联总长度Am=32+20+20=72，关联数为1对应的pi=2/72；关联数为4对应的pi=4/72；关联数为5对应的pi=5/72。

3.3 2种编配模式下装备保障机构的整体能力

综合模式1和模式2的时效性及质量性计算结果，得出2种编配模式下装备保障机构的整体能力评价结果，如表1所示。

表1 2种编配模式下装备保障机构整体能力评价结果

由表1可知：装备保障机构按模式1编配时，其时效性更优；按模式2编配时，其质量性更优；当时效性和质量性取相同权值进行整体能力评估时，模式2更优。由此可见：按装备保障行动编配机构所得整体能力更优，该种编配模式下每个机构对所有装备保障分队履行相应的保障职能，业务熟练、节约资源、效率更高，符合数字化部队模块化编组的思想，便于完成信息化条件下部队装备保障任务，可以作为部队装备保障机构编配的参考依据。

4 结论

针对当前缺乏部队装备保障机构编配模式研究的现状，笔者引入信息熵理论，从定量化的角度对装备保障机构编配模式进行了研究,建立了2种师级装备保障机构编配模式能力评价模型，并进行了比较，结果表明：装备保障机构按保障行动来设置，所得机构整体能力更高。需要指出的是，本文的研究是建立在时效性和质量性同等重要的基础上，而在实际应用中，二者的影响应该根据具体情况有所不同，下一步将对合理量化二者的影响因子展开深入研究。