摆锤杠杆式海浪发电装置摆锤杠杆结构的有限元分析

沈永辉， 王 涛

(河北工业大学， 天津 300130)

1 研究背景

进入21世纪，随着传统能源如天然气、石油和煤炭等资源的日益枯竭，据保守估计，按现在的消耗规模，全球煤碳还能开采100年,天然气还够使用55年，而石油只能使用40年[1]，而且这些能源不仅可以作为能源使用还可成为工业原料，应用到各种产品中，如在塑料、药品、化肥等都有应用，单作为能源使用非常可惜[2]。并且人类对能源的需求与日俱增，传统能源已无法满足人类生活生产的需求，这就要求人类必须开发新型能源[3]。为了解决能源供应在社会生产实践中的重要问题，全球各国都在努力寻找可替代的再生能源。海洋能在新能源中因其占有巨大的蕴藏量而备受关注。随着世界各国对海洋能发电的不断研究和实验，大量不同种类的波浪发电装置涌现了出来[4]。海洋能主要包括:潮汐能、波浪能、海流能(潮流能)、海水温差能和海水盐差能[5]。而其中波浪能因其研究时间早和基础理论的条件支撑，使它的开发和利用是目前研究最多的可再生能源和清洁能源之一[6]。利用波浪发电技术对波浪能进行开发和运用，将会在一定程度上缓解当前的能源危机。

世界各国已经研制出来的海浪发电装置多达数千种，一些国家不但有很多的关于波浪能量转换技术的专利，而且能够将这些先进的波浪发电装置投入到使用中，比如北美、日本和西欧一些国家。典型的波浪能量转换的装置有：Salter的“点头鸭”式、摆动式、聚波水库式和Russell 整流器式等[7]。以上几种波浪能量的转换的装置虽然在实际中有较好的稳定性,应用较多,但该装置的转换效率不高，投资费用却比其他同类装置贵，因此，只适合在欧洲、日本这些波浪能量较集中的国家。

我国沿海地区面积广阔，海洋资源丰富，开发海洋能对提高我国能源供应有巨大的好处[8]。为保障社会可持续性和能源安全以及环境问题的顺利解决，我国有必要建立更稳定的能源供应，寻找持续可再生能源和实行多元化能源供应，以减少对化石能源的依赖[9]。我国波浪能发电技术研究始于70年代末期，但从目前波浪能发电量来看，世界领先国家已经达到104kW级的水平，而我国波浪能发电量仅保持在100 kW的应用上[10]。

基于以上原因，本文将研究一种具有较高转换效率、较低成本而且简单实用的新型波能转换装置——摆锤杠杆式海浪发电装置[11]。

2 摆锤杠杆式海浪发电装置原理

对于海浪能的开发利用，本文能量转换的主要思路是将不规则运动的波浪能吸收转换成稳定连续的直线往复机械能，利用直线发电机转换成电能，再经电能的交变处理输出，最后并网发电。其中主要过程有波浪能的吸收和转换两个环节，实现这两个环节的关键是海浪发电装置机构的设计和能量转换系统的设计。

图1为海浪发电装置的结构示意图，主要由电气箱、摆锤浮球、直线发电机、固定支架、固定锚，整流器、蓄电瓶和逆变器等组成。为了适应海水水位高度不断变化的情况，装置设计了浮球升沉机构，当海平面升高或降低时，该机构的连杆将浮球提升或降低至海水水面。该装置的连杆与转盘套装，可以使得浮球能够随着波浪的变化360度自由摆动，从而保证其发电效率。固定锚可以防止装置随波浪力的冲击而漂流，实际情况下，海面位于摆锤浮球的中间位置。海浪的来回摆动，使摆锤浮球跟着摆动，通过连杆带动直线发电机发电，然后经电缆连接输送到整流器中，经整流后，输送到蓄电瓶中储存，需要时可用逆变器逆变后输出电能。

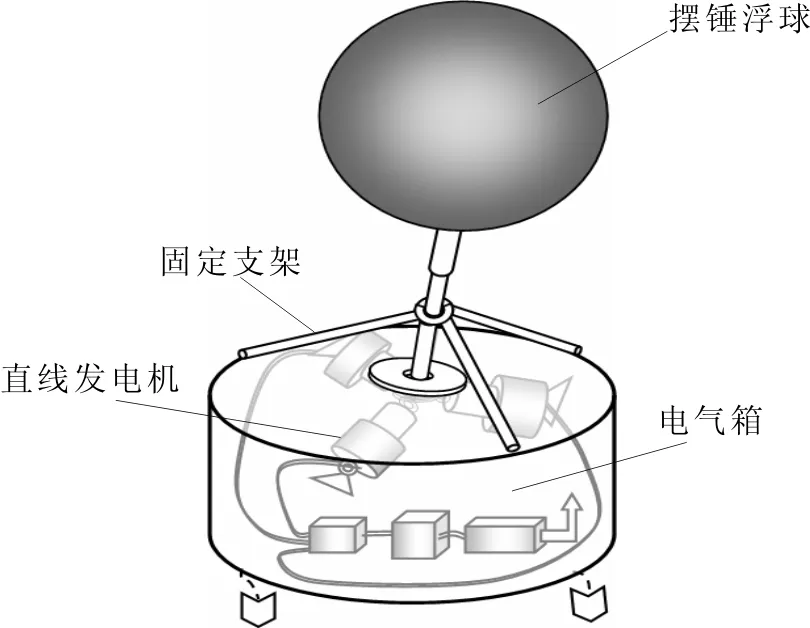
图1 海浪发电装置的结构示意图

3 摆锤杠杆在海浪中的受力分析

摆锤杠杆的运动状态与电机的各参数和波浪的高低之间存在复杂的关系[12]。本文从摆锤杠杆的受力分析人手,根据摆锤对海浪的响应,分析各参数之间的关系。

摆锤所受的浮力由自身的体积和波浪的波形决定。海浪波形受外界很多因素影响,至今仍没有任何数学模型能够精确模拟海浪波形。在一定程度上各种波浪理论只是对实际现象的简单近似，在实际工程中多应用微幅波理论作为其理论基础。

3.1 摆锤杠杆在海浪中的受力

本文选择球形体作为摆锤吸收海浪能的装置，图2为球状摆锤在海浪中的运动简图，摆锤浮球可以在一圆形区域内自由摆动，当海水受到潮水的影响，水面上升或下降时，摆锤浮球能自动竖直上升或下降，其中摆动直径的最小值为D(mm)，竖直移动的距离为L(mm)，锥形角为α(°)。以海浪发电装置的顶盖为圆心O，杠杆为z轴建立直角坐标系，则摆锤浮球形心运动轨迹在摆动直径为最小时数学模型为：

(1)

摆锤浮球形心在波浪中上升或下降运动轨迹的数学模型为：

(2)

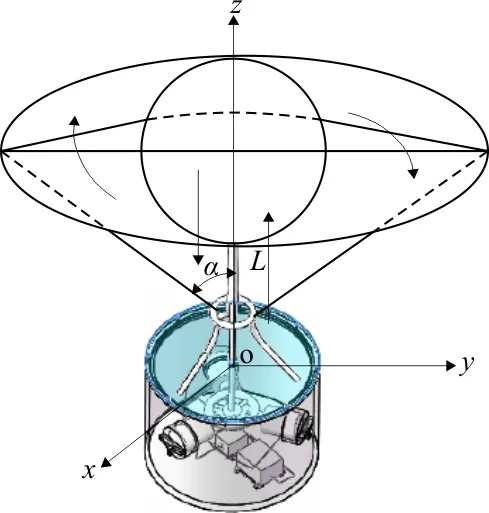
图2 海浪发电装置球状摆锤在波浪运动的轨迹

图3中虚点划线是浮球投影在yoz面上的运动轨迹，这里坐标系沿z轴上移L0(mm)，坐标原点是浮球的球心。设球形半径为R，静吃水深度为H，动出水深度为h(t)(mm),海浪的波面函数为U(y,z)，质量为G(kg)，则有：

(3)

(4)

由公式(1)～(2)得出摆锤浮球形心在yoz面上运动轨迹的对应函数分别为:

(5)

(6)

式中：ρ为海水密度，kg/m3；g为重力加速度,m/s2。

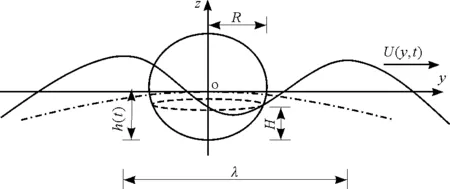
图3 球状摆锤在海浪中漂浮简图

假设某一时刻，摆锤杠杆式海浪发电装置在海浪推动下处于额定功率发电，摆锤杠杆受到海水的浮力为F浮(N)，摆锤杠杆受到的发电机的电磁阻力为F阻(N)，则摆锤杠杆受到的合力[13]∑F有：

∑F=F浮-F阻-G

(7)

为了简化计算难度，这里设其摆锤受力的合力点在摆锤形心O，且有海水的浮力F浮、发电机的电磁阻力F阻和摆锤自重G在yoz平面上，其矢量图如图4所示。

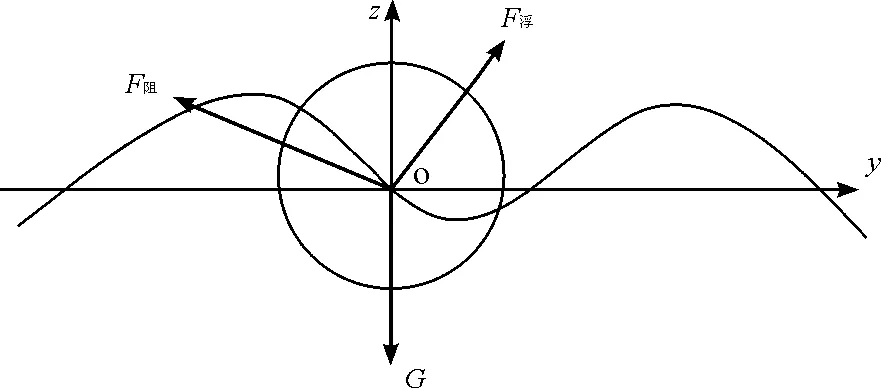
图4 球状摆锤受力简图

3.2 摆锤浮球受到海水的浮力

根据弗汝德—克雷洛夫(Froude-Krylov，简称F-K)假定法，假设摆锤浮球在海水中受到浮力是随时间t变化的矢量函数F浮=F浮(t)，它的大小和方向都随着时间的变化而变化，为了计算简便，把它正交分解，其值分别为Fy浮(t)和Fz浮(t)。分解如图5。

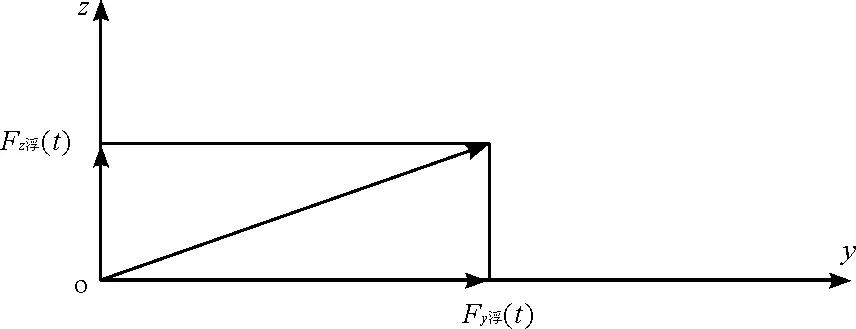
图5 波浪浮力的分解

由图5可知，摆锤浮球受到波浪竖直方向浮力Fz浮(t)和水平方向浮力Fy浮(t)，这是因为摆锤浮球沉入波浪中的部分受到海水的浮力和冲击力造成的。其中竖直方向为浮力，水平方向为冲击力。根据图4计算竖直方向的浮力有:

(8)

式中：V排(t)是摆锤浮球沉入水中部分随时间变化的函数；CV为垂直绕射系数；PZ为潜体表面任一点上未扰动入射波的波压强在垂直方向上的分量。在海浪中动态体积函数非常复杂，无法使用常规函数表达式表达，而且，在实际环境中，海浪波长远远大于摆锤浮球的半径，即λ≫R，可以把海浪波面与浮球的相交面近似成平面。为了便于计算，这里引入球坐标(R，φ,θ),则在球的表面上任意一点的球坐标为：

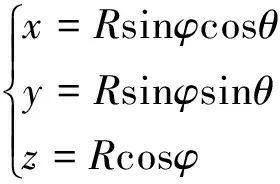
(9)

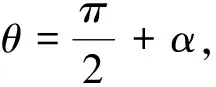
2J2(kRsinφ)cos2α]cosωt-

[2J1(kRsinφ)sinα]sinωt}

(10)

式中:h为海水深度，m；k为波数；J0(kRsinφ)、J1(kRsinφ)、J2(kRsinφ)分别是零阶 、 一阶和二阶的第一类的贝塞尔函数[15]。

分别将上式的P和 dS=R2sinφdφdθ代入公式(8)进行球面积分，得到作用在球状浮体上的垂直波浪力为：

Fz浮(t)=FV

(11)

摆锤浮球水平方向受到海浪的冲击力，一定质量(m水)(kg)的海水以一定速度(V水)(m/s)冲击浮球，单位时间的水平方向浮力(冲击力)Fy浮(t)(N)有：

(12)

式中：CH为水平绕射系数；Px为一潜体表面任一点上未扰动入射波的波压强在水平面x方向的分量。

将上式的P和dS=R2sinφdφdθ代入公式(12)进行球面积分，便得到作用在球状浮体上的水平波浪力为：

(13)

3.3 摆锤杠杆受到发电机的电磁阻力

海浪发电装置的核心部件是3台安装在电气箱侧壁的直线发电机，发电机之间的夹角为120°，分别通过螺栓与转盘连接。摆锤浮球吸收的能量先传递到杠杆上，杠杆以电气箱顶盖为支点，把能量传递给直线发电机。相反，发电机反作用杠杆一个电磁阻力F阻。图6为摆锤杠杆受到发电机的电磁阻力。

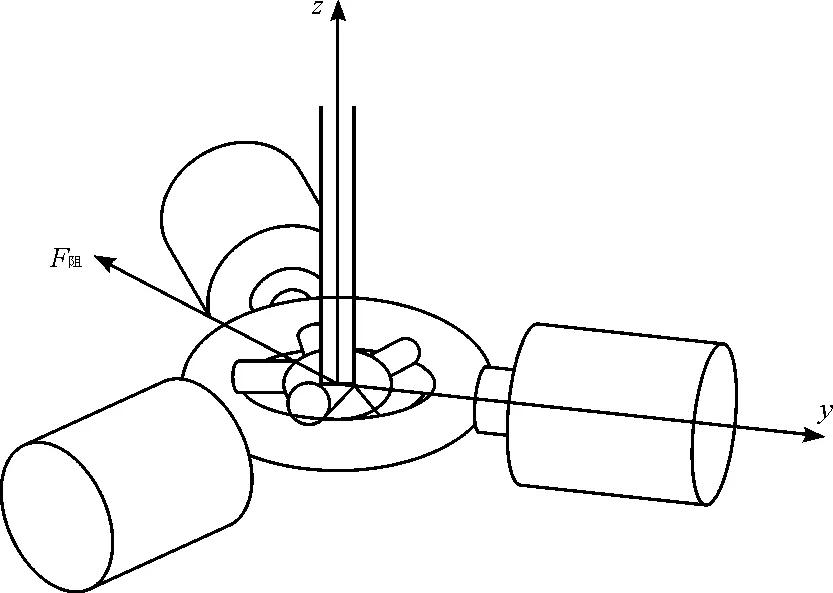
图6 摆锤杠杆受到发电机的电磁阻力

电磁阻力F阻是3台直线发电机的合力，其计算公式为：

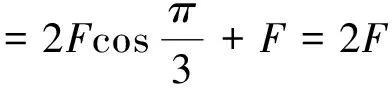
=2NBILsinθ=2NB2L2Vsinθ

(14)

式中：θ为电流与磁场方向的夹角；N为所有槽的总导体数；B为电机气隙平均磁感应强度，T；L为槽中导体的长度；V为直线动子的速度，m/s，且与摆锤浮球的切向速度成比例。

4 有限元模态分析

所谓的模态分析就是为了方便求出整个系统的模态参数，通过把线性的定常系统的振动微分方程组中的物理坐标转换成模态坐标，使得方程组实现解耦， 成为一组相互独立的方程[16]。对于模态分析，其中的振动频率ωi还有模态φi是通过下面的方程计算求出的：

(15)

式中：[K]是刚度矩阵； [M]是质量矩阵。

4.1 有限元模型的建立

在Solidworks2012创建高精度的参数化海浪发电装置模型，去除螺纹孔、圆角、倒角等对分析结果影响较小的特征[17]，然后接口导入ANSYS 软件中处理分析。由于海浪发电装置的主体结构电气箱、支撑杠杆以及保护架直接浸泡在海水中，因而使用不锈钢材料，其密度为7 750 kg/m3，杨氏模量为1.93×1011Pa，泊松比取0.31，以保证摆锤浮球正常使用。工作装置采用自由网格划分方法和四节点四面体实体单元进行网格划分，共计75 563个单元，198 323个节点[18]。

4.2 静力学分析

在静力载荷作用下分析结构的等效应力、应变等响应称为静力学分析。因海洋环境剧烈的气候条件令在陆地上使用的结构无法正常使用，对结构进行静力学分析就显得非常必要。安装在远海的摆锤杠杆式海浪发电装置的球形摆锤受到波浪力的冲击，连接摆锤的杠杆应力、应变强度必须达到许用应力、应变。摆锤、杠杆在波浪力、电磁阻力、自身重力作用下的受力过程可简化为静力平衡过程，则可以用静力学分析来求解。摆锤、杠杆受力情况随波浪力的变化而变化，在最大波浪力下施加约束和载荷。在电气箱下底面施加Fixed support固定约束，摆锤下半球面施加pressure载荷，杠杆与顶盖的接触面上施加force载荷。由于使用了轻质不锈钢合金，重力可以忽略不计，电磁阻力为系统内力。在载荷作用下求解摆锤、杠杆的应力、应变云图，如图7～8所示。

由图7得知，结构的最大应力位于杠杆靠近顶盖处和上面部分，最大应力为36.334 MPa，远小于材料允许应力 220 MPa。由图8可知，等效应变的变形量很小，不会影响装置的使用，而且，摆锤在最高工作压力下承受最大波浪力处于安全状态。

4.3 固定结构模态分析

模态分析是结构动力学分析的基础，用来求解有限自由度无外部载荷施加且无阻尼条件下运动方程的模态矩阵。这里为了使设计的摆锤杠杆式发电装置能够稳定、持续的工作，有必要对其固定结构进行模态分析，避免共振现象的发生。

用ANSYS workbench软件建立摆锤杠杆式海浪发电装置结构系统的有限元模型，分析过程使用子空间叠代法计算固有频率和振型，通过计算可得摇臂各阶模态参数，并提取前6阶模态。表1为前6阶模态频率f，图9为分析得到的结构前6阶模态振型图。

由表1可知，装置结构的最小模态频率超过100 Hz，远高于海洋波浪的振动频率，故在正常情况下装置与波浪不会发生共振现象。由图9所示振动云图知，固定支架比整体的结构刚度要小，更容易发生扭曲振动，随着阶次的增大，顶盖的振动幅度增大，装置的结构设计符合要求，能够满足远洋波浪发电。

4.4 发电装置系统模态分析

用ANSYS软件建立摆锤杠杆式海浪发电装置结构系统的有限元模型并进行模态分析。分析过程使用子空间叠代法计算固有频率和振型，提取前10阶模态[19]。前10阶固有主振型及固有频率如图10和表2所示(x轴为正视方向，y轴为纸面右侧方向，z轴为机身竖直方向)。

图7等效应力云图图8等效应变云图

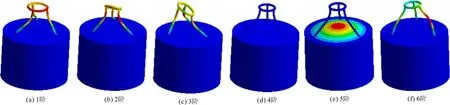
图9 结构模态前6阶振型云图

阶次12345678910频率/HZ0.180.390.401.917.867.8878.178.785.485.7

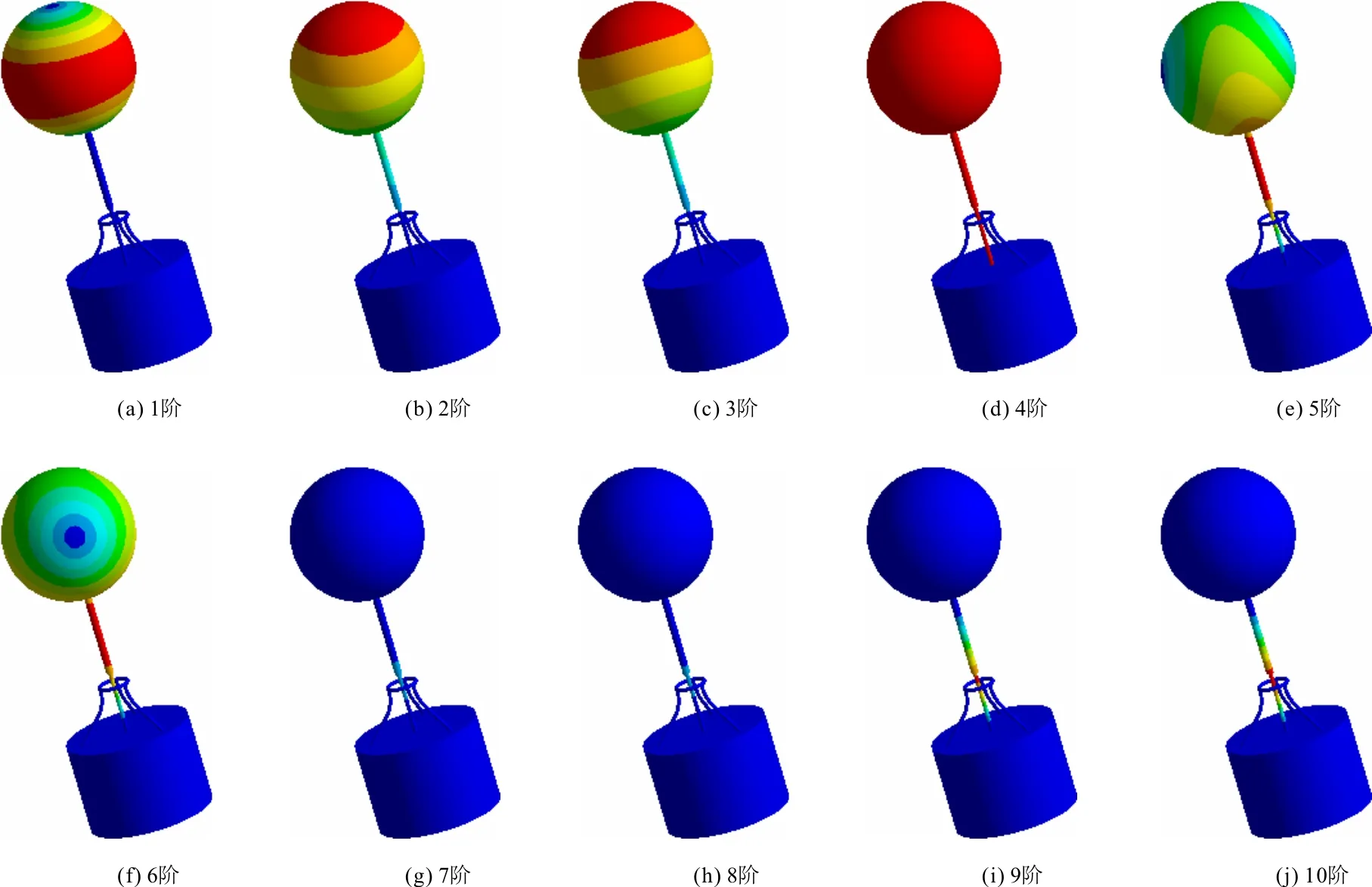
图10 摆锤杠杆式海浪发电装置整机理论模态前10阶振

由图10模态分析可以看出，真正影响摆锤杠杆式海浪发电装置的频率集中在前 6 阶上， 且前6阶固有频率都在10 Hz 之内，满足海浪发电要求。

4.5 摆锤杠杆式海浪发电装置动态谐响应分析

通过模态分析得到了摆锤杠杆式海浪发电装置结构的低阶固有频率，为了解各阶频率对结构动载荷的响应情况，需对结构进行谐响应分析。谐响应分析用于确定线性结构在承受持续周期载荷时的周期性响应，预测结构的持续动力学特性，验证其设计能否成功克服共振、疲劳及其他受迫振动引起的有害效果。当海浪冲击力的频率达到装置的某几阶固有频率时，就会使得装置在此发生共振，响应幅值显著增大。本研究使用模态叠加法，对海浪发电装置摆锤浮球表面施加海浪冲击力，频率范围在0～100 Hz 下的正弦载荷，分为50步，获得随频率变化的结构响应曲线，图11表示摆锤浮球在不同频率下的位移——频率响应曲线，图12表示摆锤浮球在不同频率下的应力——频率响应曲线。

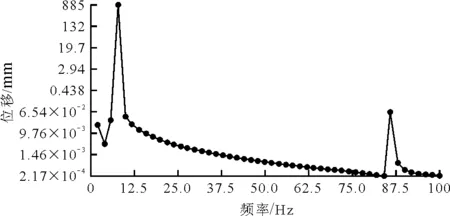
图11 摆锤浮球在不同频率下的位移响应曲线

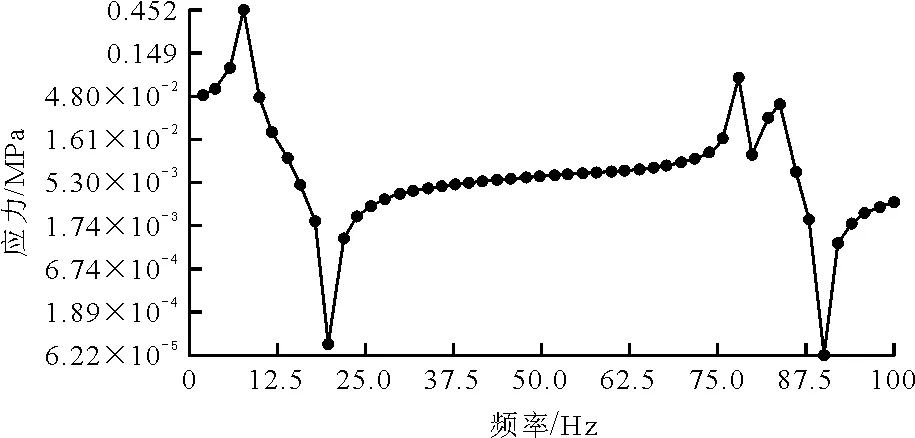
图12 摆锤浮球在不同频率下的应力变化曲线

由响应曲线可得，在不同激振频率的动载荷作用下，位移——频率响应最大峰值出现在第6阶模态频率(f=7.88 Hz )，故第6阶频易引起摆锤浮球的共振，同时应力响应值发生剧烈变化，比其他阶次的固有频率处的应力响应值大，而且此频率恰好在海浪振动频率的范围内，增大了装置吸收波浪能的效率。计算表明设计合理，符合发电要求。

5 结 论

本文在对国内外波浪发电的技术现状进行分析总结的基础上，结合海洋工程中常用的微幅波理论，提出了一种新的漂浮式波浪发电装置-摆锤杠杆式海浪发电装置，对该发电装置进行了结构设计和动态分析，并用有限元仿真软件ANSYSworkbench进行了模态分析和谐响应分析。

(1)建立摆锤杠杆式海浪发电装置三维模型，通过数学建模和有限元分析，验证了其结构设计的可行性。

(2)利用弗汝德-克雷洛夫假定法对摆锤浮球进行了动态受力分析，建立了摆锤浮球的数学模型和在海浪中运动的运动轨迹，确定了摆锤浮球的基本几何参数。

(3)利用静力学分析、模态分析、简谐振动响应分析确定了影响摆锤杠杆式海浪发电装置结构静态以及影响摆锤杠杆式海浪发电装置动态性能的关键模态频率，验证了波浪发电装置能够满足发电要求。