基于灰色局势决策和组合赋权法的再生水评价

吴梦烟， 杨 侃， 刘 朗， 梁永静， 杨 堃， 朱子唯， 卞 雨

(1.河海大学 水文水资源学院， 江苏 南京 210098； 2.句容水利农机局， 江苏 句容 212400)

1 研究背景

随着国民经济的迅猛发展，水资源消耗不断增加，水污染问题日益加剧，水资源短缺已然成为众多地区经济发展的瓶颈[1]。非常规水资源中的再生水指将污水进行适当处理并达到一定水质标准后可进行有益实用的水，是国际公认的解决城市水资源短缺的“第二水源”[2]。传统的再生水评价多集中在效益、水质和风险等单方面评估。例如，范育鹏等[3]构建了再生水利用生态环境效益评价体系，并基于此估算了北京市再生水利用的生态环境效益；汪妮等[4]建立了再生水水质评价模型, 并对西安市北石桥污水净化中心再生水水质进行评价与分析；李金娜等[5]构建了再生水风险综合评价指标体系，并以天津市纪庄子再生水厂为例进行了风险评价。但是这些评价指标体系只反映了再生水利用中某单方面的特性，指标体系单一，没有对整个再生水综合利用过程进行评价。为全面评估不同地区的再生水综合发展能力，亟待构建涵盖多种因素的综合评价指标体系。

自灰色系统理论[6]创立以来，已有众多学者将该理论中的灰色局势决策法应用于农业、环境、经济、军事和化工等诸多领域的评价研究，均取得良好结果。如曾林等[7]将灰色局势决策用于云南省中北部粳稻区域的水稻新品种综合评价；郭巍等[8]采用灰色局势决策-综合指数方法对渭河干流陕西段的水环境质量进行综合评价；王娟[9]将灰色局势决策运用于企业战略决策过程；黄贡献等[10]利用灰色局势决策法优选炮兵火力方案；经建芳等[11]基于灰色局势决策法建立了金属切削液配方决策模型。但目前还未见有学者将其应用于再生水评价中，故本文提出运用灰色局势决策法评价再生水综合发展能力。传统灰色局势决策法的白化函数存在未能覆盖所有实测值、可能丢失有用信息以及使评价结果出现误差的问题。针对该问题，本文引入指数型白化函数替代传统白化函数，对灰色局势决策法进行改进。未碧贵等[12]和马艳琴等[13]曾用指数型白化函数改进灰色聚类关联分析法，证明其可有效拓宽白化函数的覆盖范围，极大提高数据利用率。为克服传统决策权计算法只反映客观性的缺陷，采用AHP法和熵值法相结合的主客观组合赋权法确定指标权重。本文在传统灰色局势决策原理基础上，改进其白化函数和决策权的计算方法，构建了基于改进的灰色局势决策法和组合赋权法的再生水综合发展能力评价模型，并通过实例对该模型的合理性进行验证。

2 再生水综合评价指标体系

为描述再生水综合发展能力，本文结合实际情况并综合考虑水量、水质、技术、社会、效益和风险等多方面因素，建立了如图1所示的“压力-条件-影响”再生水综合评价指标体系。

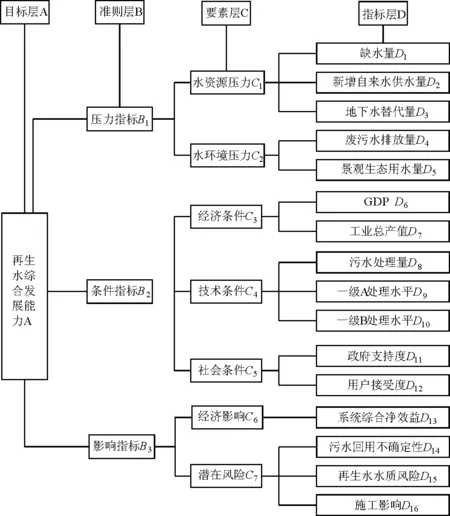
图1 “压力-条件-影响”再生水综合评价指标体系

该指标体系中，压力指标体现了现阶段开发利用再生水的需求程度；条件指标描述了现阶段再生水开发利用的经济、技术及社会条件；影响指标描述了开发利用再生水给整个社会带来的经济效益及潜在风险。

部分指标含义如下：缺水量D1指在现有供水水平下无法满足的社会需水量；新增自来水供水量D2指开发利用再生水所能增加的自来水供水量；地下水替代量D3指为解决供水不足现状而增加的地下水供水量；一级A、B处理水平D9、D10指污水处理厂所能达到的水质处理标准；系统综合净效益D13指再生水工程运行后所能取得的系统效益；污水回用不确定性D14指现有污水回用项目在运行中面临的风险和不确定性大小；再生水水质风险D15指经处理后的再生水水质的潜在风险；施工影响D16指再生水工程项目实施对周边环境造成的负面影响。在各指标中，D1～D13为正向指标，D14～D16为负向指标。其中除了D11～D12和D14～D16为定性指标外，其余皆为定量指标。

3 改进的灰色局势决策和组合赋权法的再生水评价模型

3.1 灰色局势决策法

设有n个事件a1,a2,…,an，每个事件都对应有m个决策b1,b2,…,bm，Sij表示第i事件ai用第j个对策bj处理的局势，则构成了n×m个局势，局势矩阵可表示为：

(1)

决策时运用的准则或标准即灰色局势决策中的目标可记为:T={t1,t2,…,tp}。

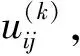
(2)

在再生水综合发展能力评价模型中，以不同地区的再生水评价作为事件i、不同发展能力等级作为对策j、不同评价指标作为目标k，计算所得的最佳决策对应的再生水综合发展能力等级即为对应地区的评价结果。

3.2 改进的白化函数

传统的白化函数为“降半梯形”结构，这种结构的函数仅考虑了相邻两个等级间评价值的关系，如果评价值在相邻等级以外，其白化函数值便会为零，这样无形中提高了相邻等级的权重，可能造成有用信息丢失，为避免出现该问题，本文引入了指数型白化函数，利用曲边代替“梯形结构”的直边，对传统的白化函数进行改进。改进的指数型白化函数曲线是平滑的，可覆盖所有范围内的实测值，从而有效解决了零权重问题[12]。传统的和改进后的白化函数分别如图2、图3所示。

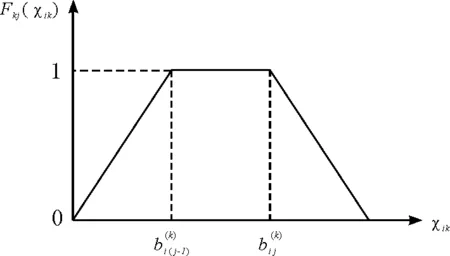
图2 传统的白化函数

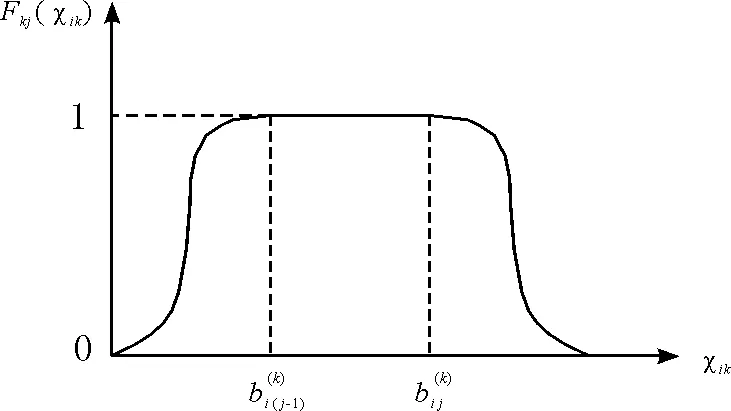
图3 改进的白化函数

当j=1时，白化函数为：

(3)

当2≤j≤m-1时，白化函数为：

(4)

当j=m时，白化函数为：

(5)

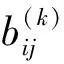
3.3 效果测度矩阵

灰色局势决策法中有3种效果测度：对正向指标使用上限效果测度，对负向指标使用下限效果测度，对中性指标即希望局势效果是在某个固定值附近的指标使用适中效果测度[7]。计算公式为：

(1)上限效果测度：

(6)

(2)下限效果测度：

(7)

(3)适中效果测度：

(8)

经上述公式标准化后，可得各目标的一致效果测度矩阵为：

3.4 组合赋权法

考虑到传统的决策权计算方法存在客观赋权法的缺点，权重计算不合理，故本文选取AHP法与熵值法计算各项指标权重，再引入距离函数对二者计算的权重结果进行组合赋权[14]，以规避两种方法各自的缺点，使最后得到的综合权重既能反映决策者的主观意向，又能合理利用客观实测数据[15-16]。

3.4.1 AHP法 根据指标体系中各指标的重要性大小对其进行评分，构造指标间两两对比的判断矩阵，通过计算，可得各指标的AHP法权重w1(k)。

3.4.2 熵值法 熵值法计算权重的步骤如下：

(1)计算不同事件i中，第k项指标下第j等级效果测度值的比重：

(9)

(2)计算不同事件i中，第k项指标的熵值：

(10)

(3)计算不同事件i中，第k项指标的熵值法权重：

(11)

3.4.3 组合赋权得综合权重 不同事件i中，第k项指标的综合权重可通过线性加权得到：

(12)

式中：α、β分别为AHP法与熵值法权重的分配系数，α+β=1。

(13)

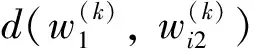
(14)

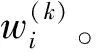
3.5 综合效果测度矩阵

由各目标的效果测度和组合权重可得不同局势Sij的综合效果测度：

(15)

所有目标下的综合效果测度矩阵R可表示为[7]：

(16)

3.6 改进的灰色局势决策和组合赋权法的再生水评价模型

模型计算和评价的过程如下：(1)基于改进的白化函数计算各指标的效果白化值；(2)计算各指标的效果测度，进而得效果测度矩阵；(3)计算各指标的AHP法和熵值法权重，引入距离函数计算综合权重；(4)计算综合效果测度矩阵；(5)根据综合效果测度值评价不同地区的再生水综合发展能力。图4为基于改进的灰色局势决策和组合赋权法的再生水评价流程图。

图4 基于改进的灰色局势决策和组合赋权法的再生水评价流程图

4 实例应用

4.1 数据收集

本文以云南省3个城市K、Y、L为实例来验证前文建立的再生水综合评价模型。各市基本情况如下：K市为地区政治、经济、文化中心，GDP及工业总产值高，缺水量大，废污水排放量大，污水处理技术较好，总之该市对开发利用再生水有较大需求且开发条件好，再生水发展能力高；Y市经济水平中等，但工业总产值占GDP比重大，工业快速发展需要大量用水，废污水排放量较大，总之该市对开发利用再生水的需求较大且开发条件较好，再生水发展能力较高；L市为以旅游业为主的城市，经济实力较差，缺水量较小，废污水排放量较小，用户接受度低，利用风险较高，总之该市对开发利用再生水的需求小且开发条件差，再生水发展能力较低。根据实际情况，3个城市再生水发展能力水平依次为：K市>Y市>L市。

收集3个城市各项定量指标数据(资料来自3个城市2016年的统计年鉴与环境统计年鉴)，定性指标由经验丰富的专家打分或问卷调查等方法定量化处理。

表1为3个城市再生水发展能力各评价指标实测值。

通过查阅相关资料、咨询专家，最终确定3个城市再生水评价各项指标的分级标准，见表2，每个指标都划分为五个等级，一级为最优，五级为最差。

表1 3个城市再生水评价指标实测值

表2 评价指标分级值

4.2 数据处理

步骤1：先用3.2节中改进的白化函数公式计算各指标对应不同等级的白化函数值，根据指标特性，用3.3节中的上限效果测度公式计算D1～D13的效果测度值，用下限效果测度公式计算D14～D16的效果测度值。计算结果见表3。

步骤2：分别计算各指标的AHP法权重w1(k)和对应3个城市的熵值法权重wi2(k)；再根据距离函数求出分配系数α、β，对w1(k)和wi2(k)进行线性加权，求得3个城市各指标的综合权重wi(k)，此处i=1,2,…,3，k=1,2,…,16,计算结果见表4。

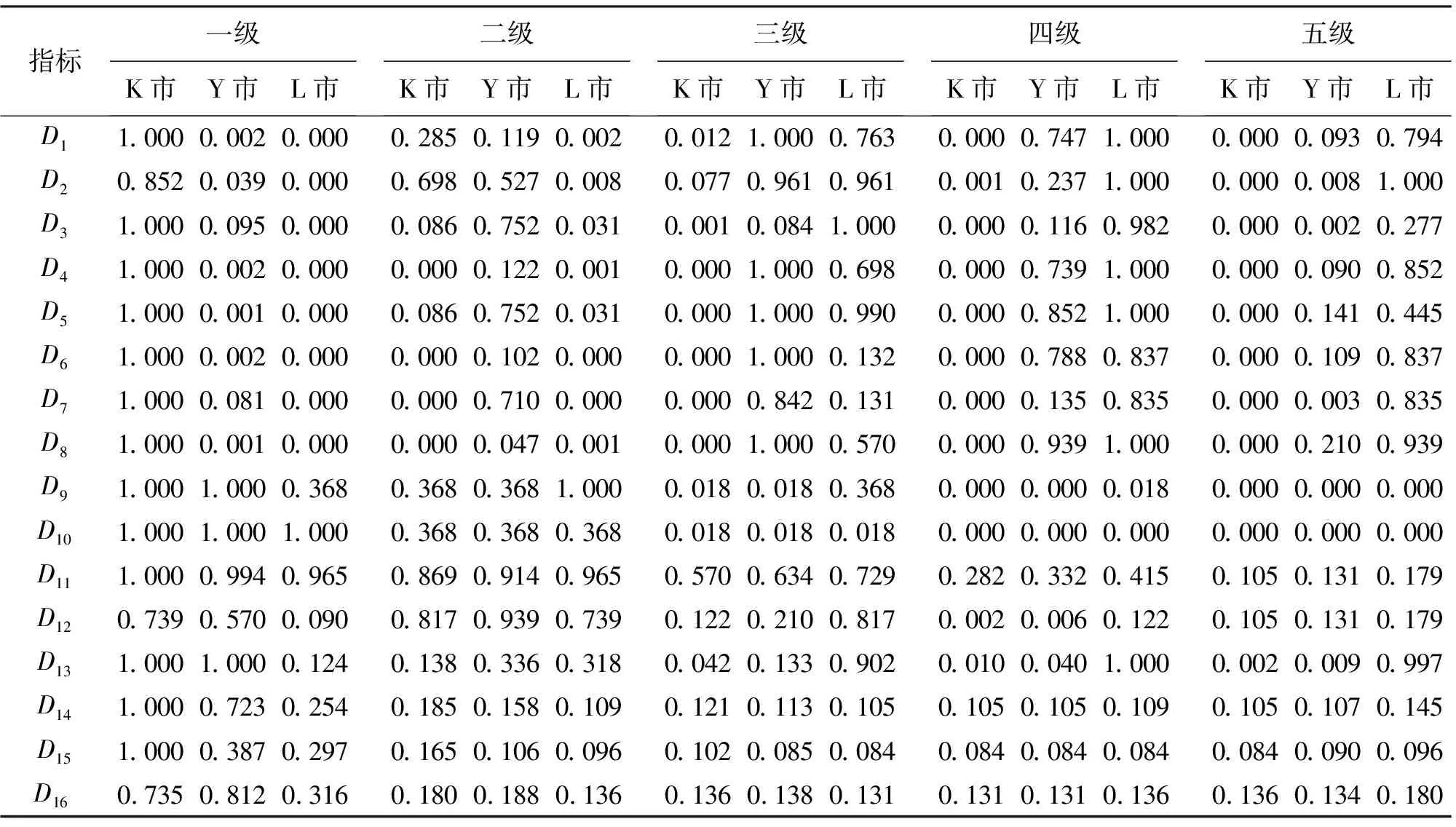
表3 3个城市各指标效果测度

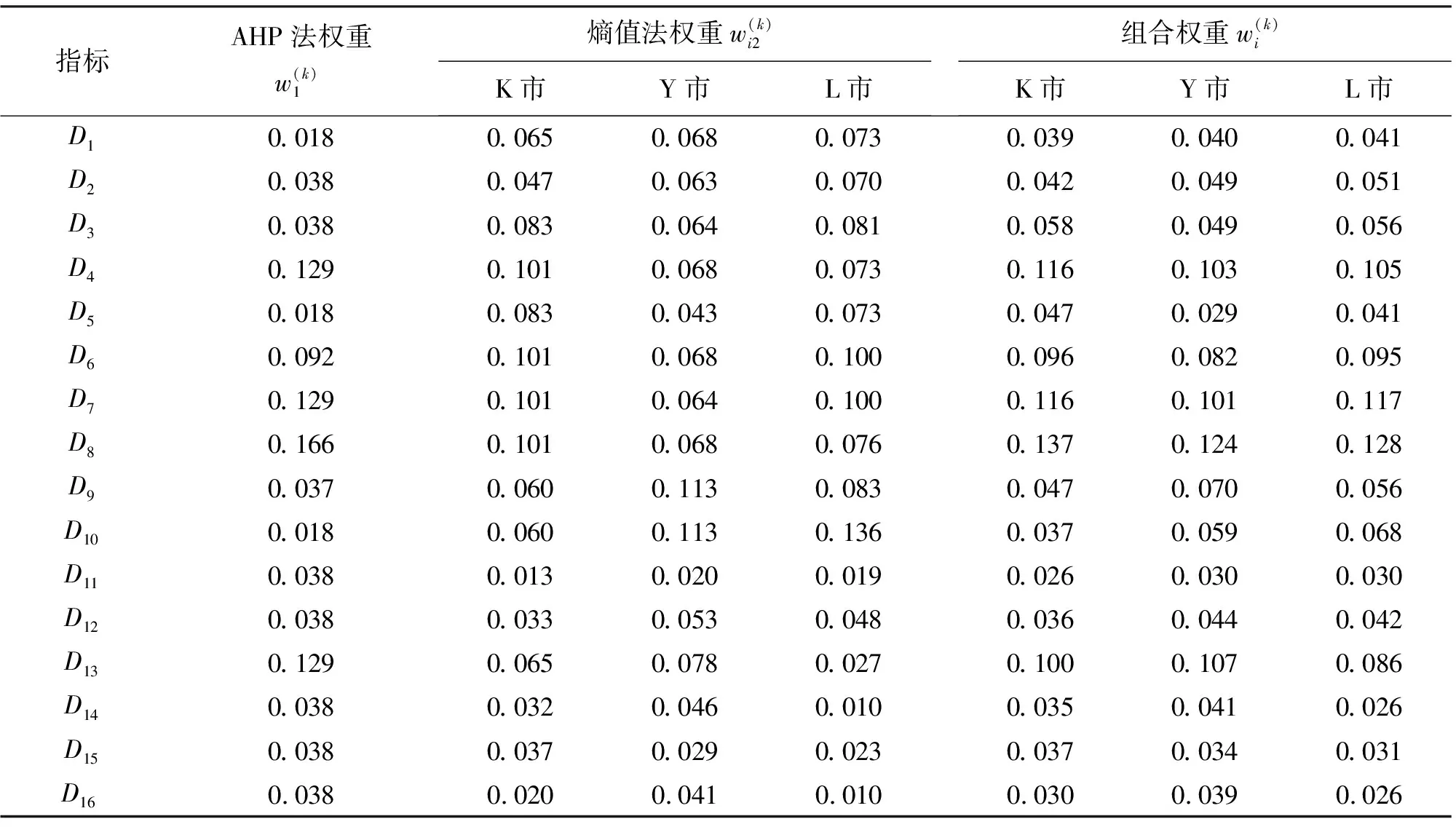
表4 3个城市各指标组合权重

步骤3：根据公式(15)计算各市的综合效果测度，结果见表5。

4.3 结果分析及建议

根据最佳效果准则，由表5可知，K市的再生水综合发展能力为一级，Y市为三级，L市为四级。计算结果表明K市再生水综合发展能力最强，其次为Y市，L市的再生水发展能力最弱，这与各市的实际情况一致，说明本文构建的基于改进的灰色局势决策和组合赋权法的再生水综合评价模型具有合理性，能够正确反映各市再生水利用的综合发展能力。

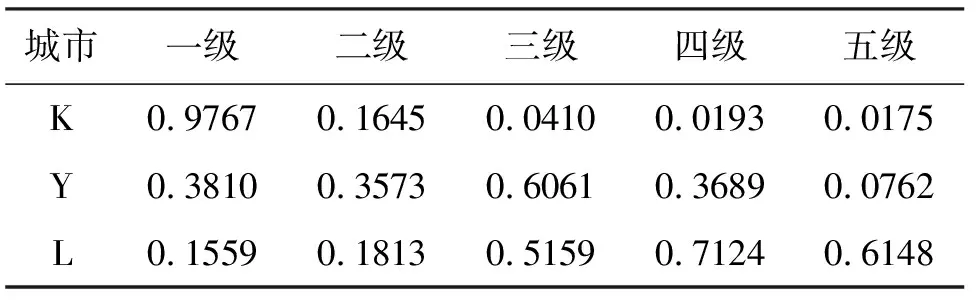
表5 3个城市再生水综合评价结果

进一步对各市的16项指标值进行分析，K市不仅缺水情况最为严重，而且废污水排放量达5.38×108t，远大于其他城市，且经济和社会条件俱佳、污水处理水平高，再生水综合发展能力高，达到一级水平，故建议该市优先发展利用再生水；Y市水资源压力和经济技术水平都小于K市，再生水综合发展等级处于三级，但由于该市大力发展工业，废污水排放量较大，水环境压力大，且综合实力不弱，故建议Y市也可逐步发展利用再生水；L市的用水、水环境等各方面压力与其它二市相比皆较为缓和，经济技术条件还有待提高，用户接受度低，且受技术水平限制，开发利用再生水还存在较大的潜在风险，故再生水综合发展力等级为四级，建议现阶段可先不着重于发展再生水。

5 结 论

(1)建立的再生水综合发展能力评价指标体系克服了目前再生水评价模型中存在的评价指标单一的缺点。

(2)首次提出将灰色局势决策法应用于再生水评价，并引入指数型白化函数对传统的“降半梯形”白化函数进行改进，有效解决了可能出现的白化函数值为零、易丢失有用信息的问题。

(3)采用主客观相结合的组合赋权法计算各项指标权重，解决了传统决策权计算方法过于依赖实测数据，权重计算不够合理的问题。

(4)建立起基于改进的灰色局势决策和组合赋权法的再生水综合发展能力评价模型。

以云南省K市、Y市、L市的再生水综合发展能力为例开展计算分析，3个市的再生水综合发展能力大小为K市>Y市>L市，计算结果与实际相符，表明本文构建的指标体系完整，模型正确，计算分析方法可行，在再生水综合发展能力评价方面具有实际可行性和有效性。