库水位缓变作用下高陡边坡变形及稳定性分析

余志刚，蒋博林，莫勇刚，阴 可

(1.重庆工程职业技术学院建筑工程学院，重庆402260；2.重庆大学土木工程学院，重庆400045；3.山地城镇建设与新技术教育部重点实验室，重庆400045)

0 引 言

库岸滑坡主要是由于水位升、降引起边坡所受到的水力条件频繁变化而产生的。水库蓄水后，水位升、降对边坡的失稳有显著影响。MORGENSTERN[1]报道了16起土坝迎水面由于水位骤降引发的滑坡；ROOSEVELT湖附近地区1941年～1953年发生的滑坡表明[2]，49%发生在1941年～1942年的蓄水初期，30%发生在水位骤降10～20 m期间，21%发生在其他时间(小型滑坡)；在日本，约40%的水库滑坡发生在库水位上升期间，包括初期蓄水，60%发生在水位骤降期间。对库水位升、降引起的边坡失稳机理及稳定安全系数变化特征的研究表明，库水位升、降对边坡稳定性影响较大[3]，对水-岩循环作用的研究都反映出其对岩体有较大弱化作用[4]，水位的升、降对岸坡渗流场及浸润线分布变化有显著的影响[5- 6]。现虽以“库水升、降作用”命名的相关文献较多，但几乎都是在假定降水前边坡状态一致的前提下计算初始应力场的，而涉及某一因素，如渗透系数[7]、土-水特征曲线[8]在升、降水全过程中对岸坡变形及稳定性的影响的研究很少。

研究水位缓变时岸坡变形及稳定性主要优点在于充分考虑了时间效应的影响。为此，本文选用Geo-Studio系列有限元软件 SLOPE/W、SEEP/W及SIGMA/W 进行耦合模拟，分析升、降水全过程条件下近似平行坡面裂隙及渗透系数对边坡变形位移及稳定性的影响效应，以及单独升、降水条件下渗透系数对边坡稳定性的影响规律。

1 地下水位升、降函数的影响因素

根据包辛涅斯克(Boussinesq)非稳定渗流运动的微分方程，可采用简化方法推导得到边坡岩体距离库岸水平位移x位置处在t时刻的地下水位升、降函数[9]，即

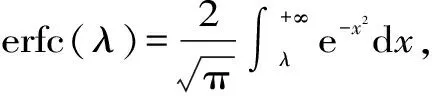
上述结论只有在升、降水前，岸坡浸润线及岩体力学状态都一致的条件下才能成立。虽仅考虑浸润线的位置一致，不考虑岸坡岩体力学状态是否一致不符合工程的实际情况，但从较宏观角度，对库水升、降作用相关研究仍有较大借鉴意义。分析可知，库水位上升时，对边坡的稳定有利可以改变以下条件：增大V或μ、减小k或H。库水位下降时，对边坡的稳定有利可以改变以下条件：减小V或μ、增大k或H。

2 数值试验方案设计

2.1 数值模型

某水库最大坝高约109 m。坝址处属深切中山地貌，为左陡右缓不对称的“U”形河谷，左坝肩陡崖绝，存在2条主要近似平行坡面的裂隙X1、X2，裂隙X1倾角75°～85°，张开达15～35 cm，局部粘土充填；裂隙X2最大宽度约45 cm，基本无充填。数值模拟计算模型见图1。岩体物理力学参数见表1。

图1 数值模拟计算模型

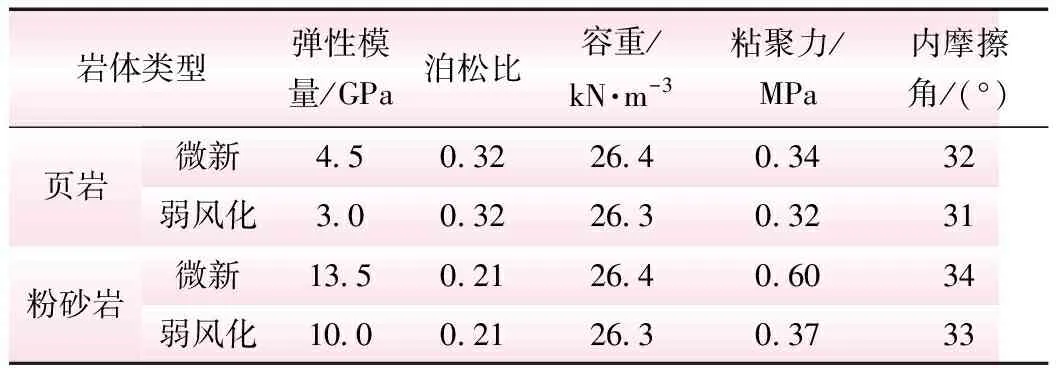
表1 岩体物理力学参数

2.2 升、降水速度

库水位升、降速度见表2。计算水位基面采用库底位置处作为计算水位的零点，最高上升水位为98 m。虽然岸坡水位在53、98 m持续365 d内因水位高度不变而提供的坡面应力不变，但考虑岸坡岩体存在一定的渗流力的作用，故将此阶段变形看成近似蠕变。

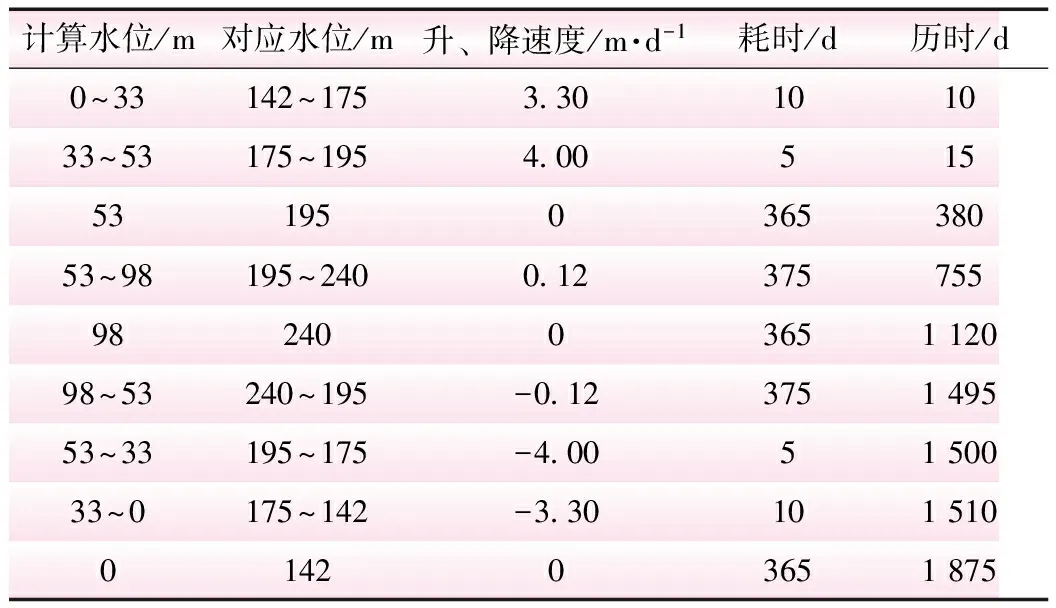
表2 库水位升、降速度

2.3 模拟条件

数值模拟条件见表3。表中，Ci-S为缓变时第i种条件，i=1、2、3、4、5。统一取值指的是岩体渗透系数都取1×10-4cm/s；分区域取值指的是弱风化线底界线以上的岩体渗透系数取1×10-2cm/s，弱风化线底界线与弱透水层顶界线之间的岩体渗透系数取1×10-3cm/s，弱透水层顶界线以下的岩体渗透系数取1×10-4cm/s。

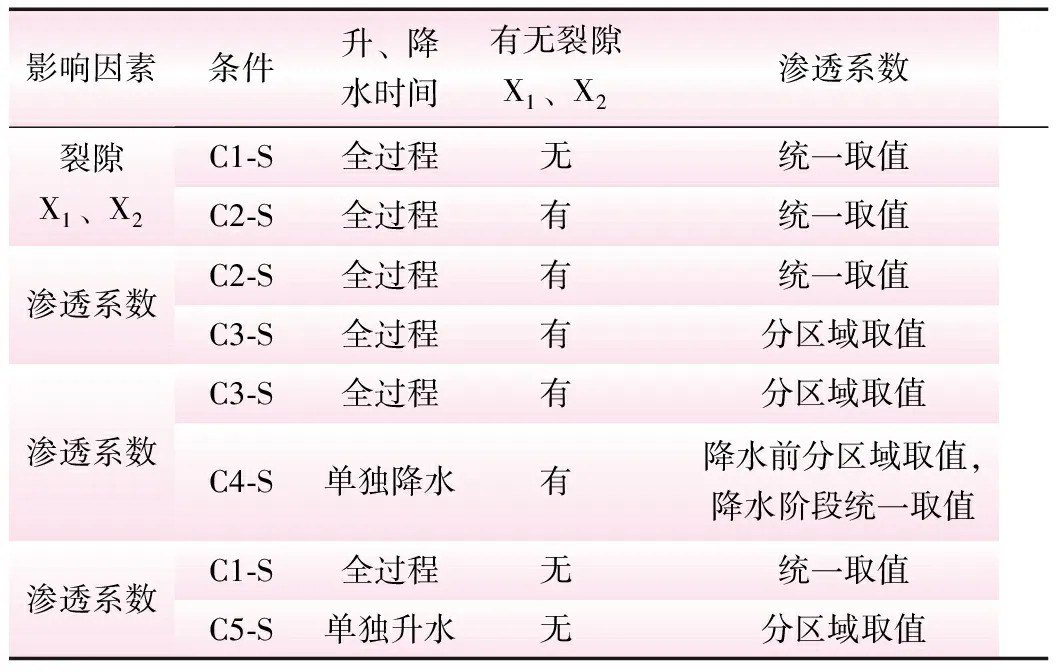
表3 数值模拟条件

2.4 观测点

在整个边坡坡面，按高度划分坡面上部1/3高度、坡面中部1/3高度及坡面下部1/3高度3个部分进行位移观测，每个部分从高到低依次选取14个观测点进行编号：第1～14观测点，相邻观测点高差约4～5 m，裂隙X2左侧及右侧从高到低依次取8、7个观测点，相邻观测点高差约8～9 m。坡面中部1/3高度内观测点布置见图2。

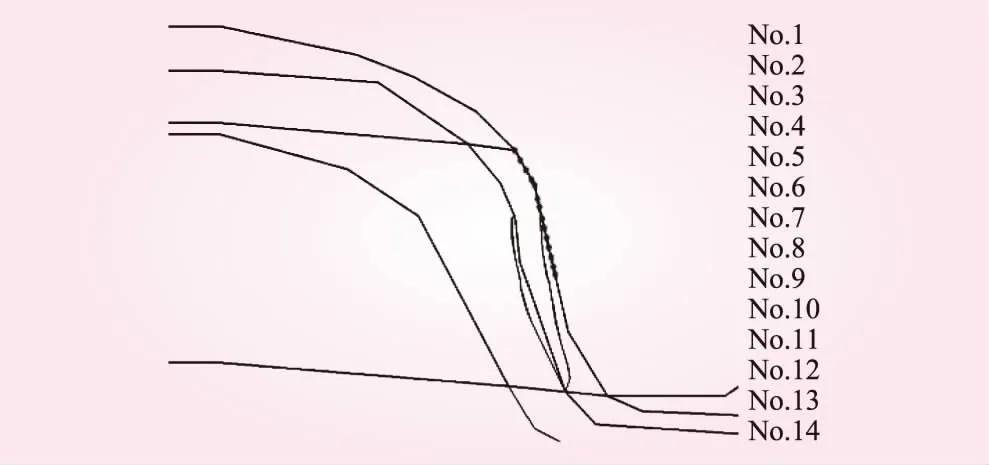
图2 坡面中部1/3高度内观测点布置

3 数值试验结果分析

3.1 位移分析

选取坡面中部1/3高度内第1、12、14观测点的位移为例进行分析，其水平位移-时间关系见图3，观测点的位移-时间关系极值见表4。

图3 位移-时间关系

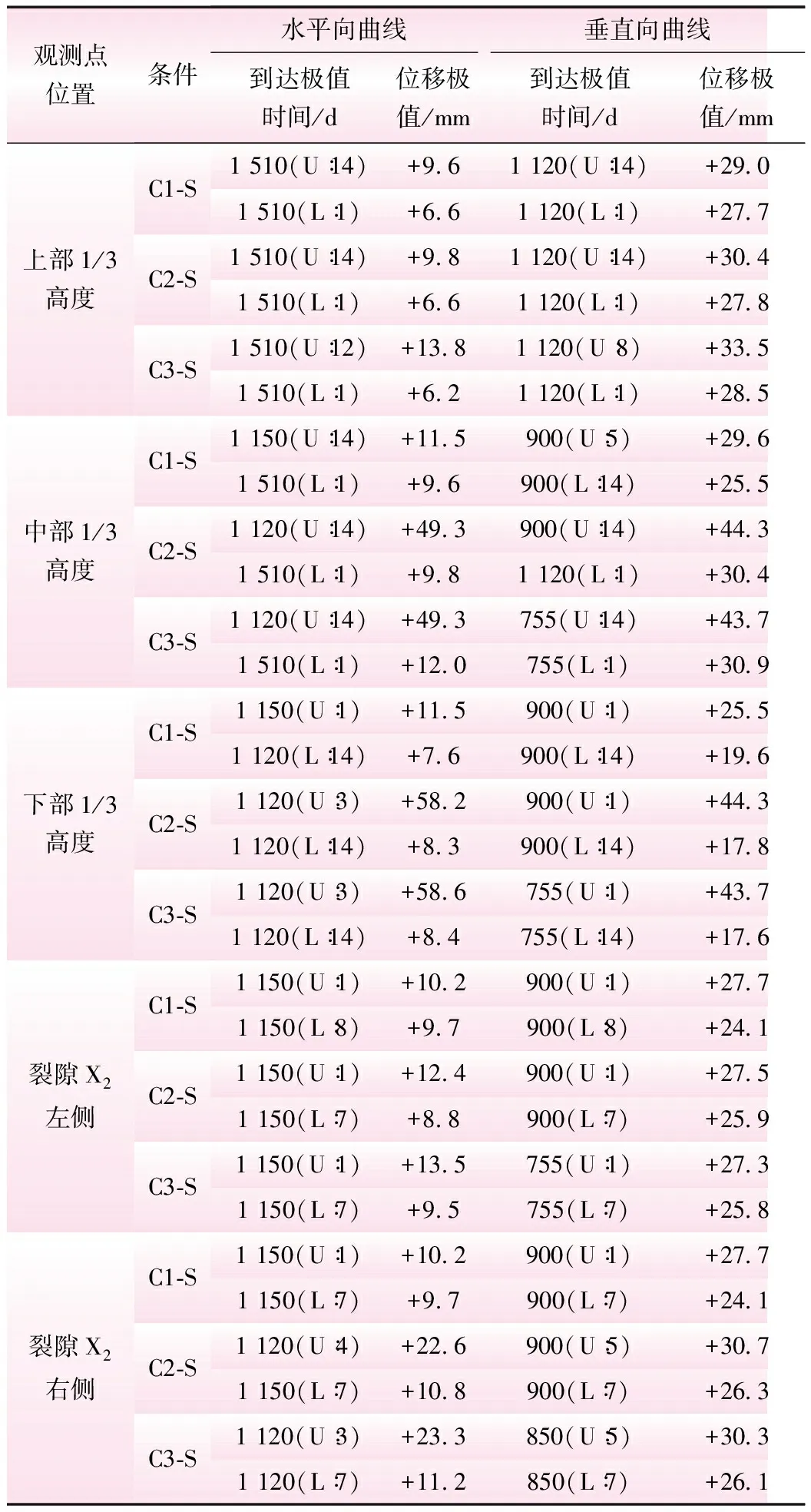
表4 观测点的位移-时间关系极值

注：U为最高位置的曲线，如U∶14表示最高位置是第14号曲线，L为最低位置的曲线，如L∶1表示最低位置是第1号曲线。

从图3和表4分析可知，有裂隙X1、X2时的影响，对坡面上部1/3高度及裂隙X2左侧内观测点X、Y向位移影响较小，对中部1/3高度、下部1/3高度及裂隙X2右侧内观测点X、Y向位移影响都较大，下部1/3高度、裂隙X2左侧及右侧内观测点整体都表现越高越敏感，上部1/3高度及中部1/3高度内观测点整体都表现越低越敏感，下部1/3高度内观测点整体位移表现最敏感。各测区观测点近似蠕变规律虽稍有差异，但有裂隙时对其影响规律类似各测区整体位移变化规律。增大渗透系数时对所有观测点的X、Y向位移影响都较小，观测点的敏感性及近似蠕变规律与有裂隙时几乎一致。

3.2 岸坡稳定安全系数分析

采用极限平衡分析法中的摩根斯顿-普赖斯法(Morgenstern-Price)[10]进行岸坡稳定计算，岸坡稳定安全系数-时间关系见图4。

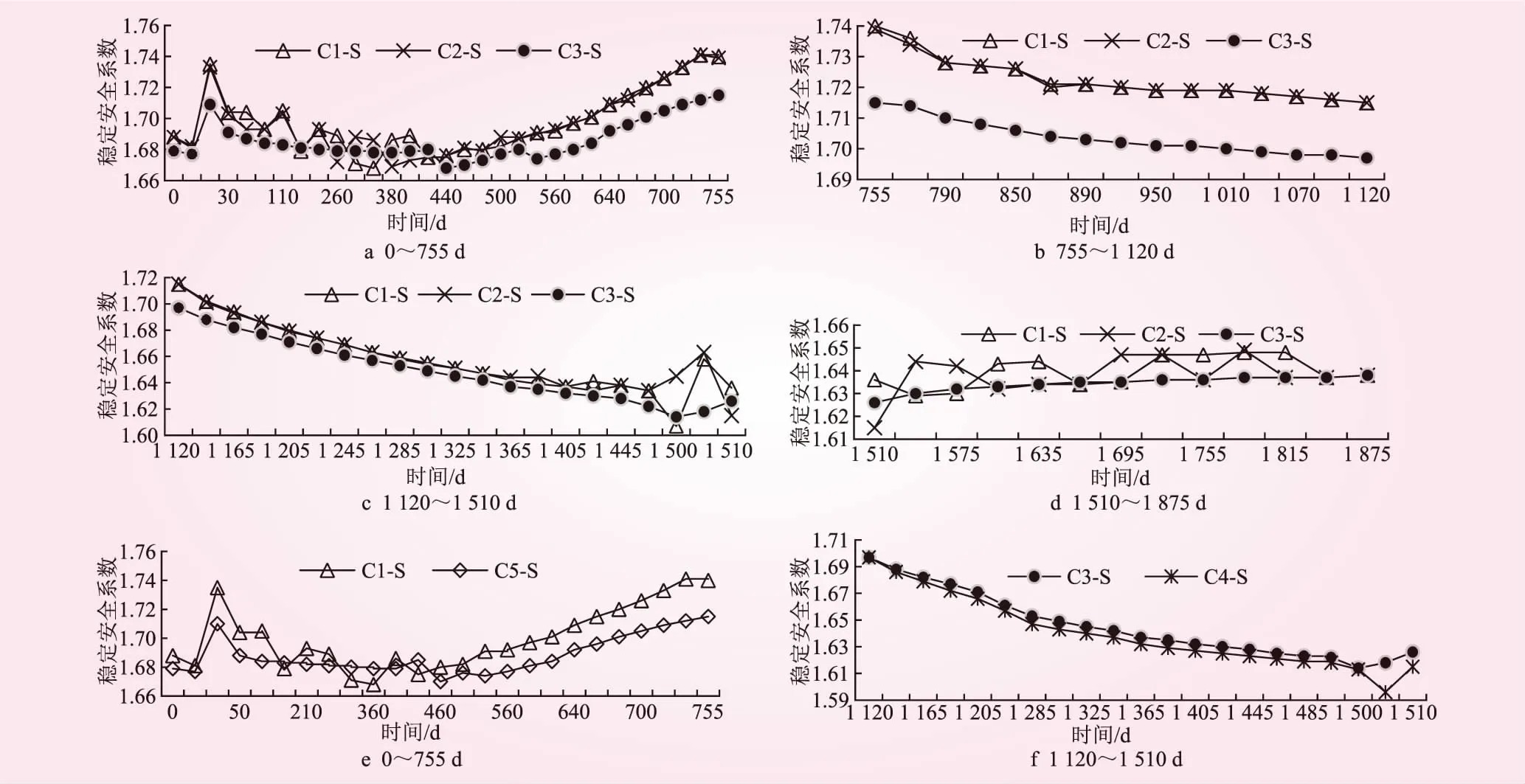
图4 岸坡稳定安全系数-时间关系

从图4可知，有裂隙X1、X2时，与C1-S时对比，C2-S时稳定安全系数几乎一致，其值普遍大于1.60。增大渗透系数时，与C2-S时对比，C3-S时其值整体表现都有下降趋势，单独升水时，渗透系数越大，稳定安全系数越小，裂隙的存在不影响此规律。全过程升、降水时，在水位下降阶段渗透系数越大，稳定安全系数越小。单独降水时，渗透系数越大，稳定安全系数越大。

C2-S、C3-S时稳定安全系数虽然都普遍大于1.60，但观测点位移值却较大，如C3-S时坡面下部1/3高度内观测点X、Y向位移最大值达58.6、43.7 mm。本文倾向认为，距离库底28～72 m高度内坡面岩体位移较大，稳定性较差；而剩余坡面附近岩体及坡体内部岩体整体稳定性都较好。

4 结 语

本文基于Geoslope软件，分析升、降水全过程条件下近似平行坡面裂隙及渗透系数对边坡变形位移及稳定性的影响效应，以及单独升、降水条件下渗透系数对边坡稳定性的影响规律，得出以下结论：

(1)有近似平行坡面裂隙时，对坡面上部1/3高度及裂隙X2左侧内观测点X、Y向位移影响较小，对坡面中部1/3高度、下部1/3高度及裂隙X2右侧内观测点X、Y向位移影响都较大，对边坡稳定安全系数几乎无影响。

(2)增大渗透系数时，对所有观测点的X、Y向位移影响都较小；在升、降水全过程时，岩体渗透系数越大，各阶段稳定安全系数越小；在单独升水时，渗透系数越大，稳定安全系数越小，近似平行坡面裂隙的存在对此规律无影响；在单独降水时，渗透系数越大，稳定安全系数越大。今后应重视库水位升、降全过程中影响因素对边坡的全动态过程的影响。

(3)有近似平行坡面裂隙或增大渗透系数时，下部1/3高度、裂隙X2左侧及右侧内观测点整体都表现为越高越敏感，上部1/3高度及中部1/3高度内观测点整体都表现越低越敏感，各测区观测点近似蠕变规律类似各测区整体位移变化规律。

(4)对边坡稳定性分析不能完全依赖于稳定安全系数的求解，应结合观测点位移进行综合分析评价，才能得出比较可靠的结论。