基于密集度的虚拟力节点部署算法*
2018-07-20滕志军郭力文吕金玲东北电力大学信息工程学院吉林吉林132012
滕志军,张 力,郭力文,吕金玲(东北电力大学信息工程学院,吉林 吉林 132012)
近年来,具有高度的灵活性和集成功能多样化的可移动无线传感器网络WSNs(Wireless Sensor Networks)在军事侦察、环境监测以及防爆救灾等领域得到广泛的应用[1-4]。而移动传感器网络节点的初次部署通常为随机抛撒,很难实现对监测区域的覆盖需求,因此采用适合的节点部署算法进行再部署以满足应用需求[5-7]。
目前,关于节点部署算法已有大量的研究成果,包括基于计算几何理论的相关算法,如基于Delaunay、Voronoi 等网格划分分析方法[8];集中式算法,如遗传算法、蚁群算法、粒子群算法等;以及基于虚拟力的节点部署算法[9-10]。文献[11]首次提出基于虚拟力的节点自主部署算法VFA(Virtual Force Algorithm),并分别考虑了二元感知模型以及概率感知模型。文献[12]在传统VFA的基础上考虑了监控区域的目标特性,节点不仅受到节点间的相互作用力外还受到目标位置的引力作用。文献[13]引入了“引力线”的概念,构建了节点与引力线之间的斥力以此减少了节点的能量消耗,缩短了部署时间。文献[14]将传统VFA的动态部署分成簇间和簇内两个阶段以此改善VFA中出现的簇间干涉,节点受力均衡的问题。文献[15]结合计算几何重新定义了节点间的邻接关系,从而保证了区域的覆盖质量。文献[16]在VFA的思想上,针对同构节点、异构节点、非规则区域等各种应用场合,研究了基于粒子均衡的移动传感器网络覆盖,取得了较好的覆盖效果和网络生命周期。
但现有基于虚拟力的节点部署算法对虚拟力模型的相关参数研究相对较少,在无法判断随机部署的情况下,仅仅根据经验值设置虚拟力模型的相关参数,对部署效果产生了一定的影响。因此,本文提出基于密集度的虚拟力节点部署算法IVFA-B(Intensity-based Virtual Force Algorithm with Boundary Forces)采用公式推导的方式优化虚拟力相关参数,并定义了节点的密集度以此来选择虚拟力模型中的最优距离阈值,通过仿真实验证明了IVFA-B算法对提高网络覆盖质量的有效性。
1 问题与假设
假设在A×B监测区域内随机抛撒N个移动传感器节点。节点的感知半径均为Rs,通信半径均为Rc,并满足Rc≥2Rs。节点感知模型均采用布尔感知模型,并对无线传感器网络参数进行如下假设:①每个传感器节点均具有充足的能量,并与移动执行器相结合,可以在监测区域内移动到最佳位置;②每个传感器节点都可以通过GPS或者其他的相关定位算法获取到自身的位置信息和自身与其邻居节点间的位置关系;③每个传感器节点可以感知并获取在其通信半径范围内其他传感器节点的位置。
相关定义如下:
定义1布尔感知模型[17]
传感器节点si(xi,yi)以自身坐标(xi,yi)为圆心,以感知半径Rs作为感知区域半径构成其最大感知范围,即为布尔感知模型。二维平面内任意一点p(x,y)与传感器节点si之间的欧式距离记为
(1)
若d(si,p)≤Rs,则点p(x,y)被覆盖,节点si对点p的感知概率为1,否则为0,公式如下:
(2)
定义2覆盖率[18]
传感器节点已经覆盖的区域面积大小As与监测区域的总面积大小A之比为覆盖率,记为a,定义为:
a=As/A
(3)
定义3平均移动距离[19]
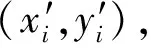
(4)
定义4密集度
节点的密集度代表其所在区域的密集程度,公式如下:
(5)
式中:N为si的邻居节点个数,din为邻居节点sn到si的距离。对于一个节点来说,它的相邻节点个数越多,它与相邻节点之间的距离越小,该节点的密集度越大,则表明这个节点所在区域越密集。
2 基于密集度的虚拟力节点部署算法
2.1 算法涉及的虚拟作用力
①节点间的相互作用力
(6)
式中:dij表示节点si与节点sj之间的欧氏距离,αij表示节点si到节点sj线段的方向角,ωa/ωb分别表示虚拟力引力/斥力系数,Dth表示节点间距离阈值,Rc表示节点的通信半径。
②区域边界对节点的斥力
dib表示节点si与区域边界之间的欧式距离。节点与区域边界的安全距离为dth/2。如果dib大于节点与区域边界的安全距离,则不存在斥力作用;如果dib小于节点与区域边界的安全距离,则表达式如下
(7)
(8)
③节点所受虚拟力合力
(9)
式中:k表示si的邻居节点数目。
无线传感器节点在虚拟力Fi作用的约束下,将按照以下方式从原有位置P(xiold,yiold)移动到目标位置P(xinew,yinew)。
(10)
式中:Fx和Fy分别表示在x轴和y轴方向上传感器所受力的投影,Fxy表示传感器所受到的合力,Maxdis表示传感器单次移动的最大距离。
2.2 虚拟力参数
在传统虚拟力节点部署算法中,wa,wb分别表示虚拟力引力参数和斥力参数。由于数目较少的邻居节点之间存在斥力作用,数目较多的非邻居节点之间存在引力作用,为使节点达到平衡状态,从而将斥力参数设置地远大于引力参数。但在事先无法判定随机部署状态的情况下,仅仅根据经验值设置一个较大的斥力参数和一个较小的引力参数,不能达到很好的覆盖效果。为此,本文给出一种解决方案,通过对节点进行受力分析,从而推导出ωa与ωb的关系式。
如图1所示,对节点si进行受力分析。
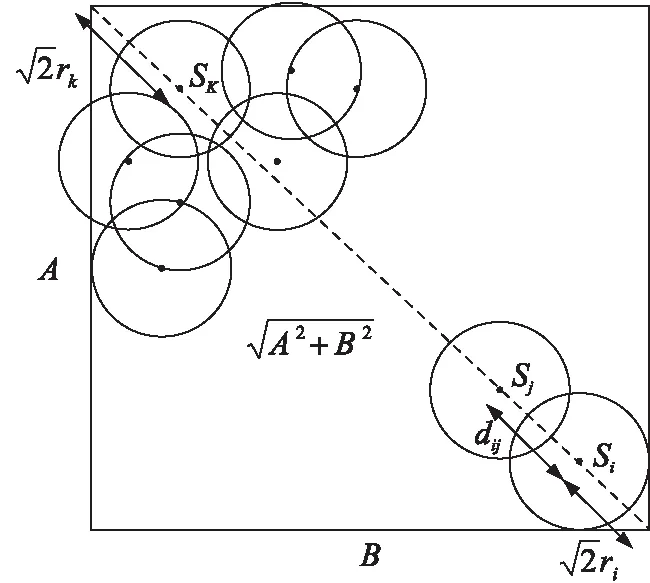
图1 极端节点分析图
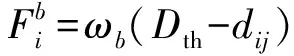
(11)
(12)
(13)
当节点si受力平衡,达到稳定状态时,
(14)
由于区域边界对节点同样为排斥力,区域边界斥力参数为ωr,最终得到引力/斥力参数的表达式为:
(15)
ωa=Dth-dij
(16)
2.3 距离阈值
通过分析经典虚拟力模型,得出距离阈值可以调节传感器节点间的相互作用力属性。而距离阈值的设置不仅与节点感知半径有关,也与邻居节点分布之间有着密切的联系。同时,节点的相邻节点数和与其相邻节点的距离共同影响监测区域内节点分布的密集程度。因此,判断节点所在区域的密集程度可以通过衡量每个节点的相邻节点数目以及与相邻节点间的距离来判断。
图2为2组不同的环境设置条件下的距离阈值设置分析图。图2(a)覆盖率a<1,表明节点没有完全覆盖整个监测区域,故距离阈值设置为两个节点的感知半径之和。图2(b)覆盖率a≥1,表明节点足够覆盖整个监测区域,最佳部署为正三角形部署,因此距离阈值的设置如式(17)。
(17)
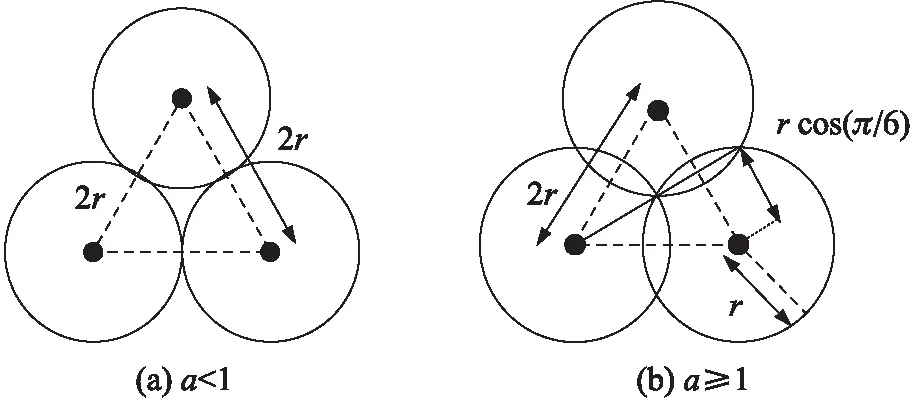
图2 距离阈值分析图
2.4 算法伪代码
基于上述分析,本文通过合理设置虚拟力相关参数并且利用节点的密集度选择最佳距离阈值,从而提出了基于密集度的虚拟力节点部署算法(IVFA-B),该算法可以更好地实现全局的覆盖优化,并提高了虚拟力算法性能。算法实现的伪代码如表1所示。
表1IVFA-B算法的伪代码

3 仿真结果与性能分析
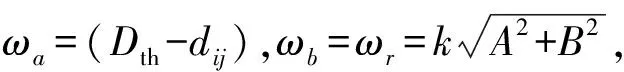
图3显示了4种算法对35个节点的部署情况,其中图3(a)为网络中节点的初始分布情况,初始覆盖率为65.4%。图3(b)为应用VFA算法的节点分布情况,节点分布有所提高,但可以看出部分节点移出到边界外。图3(c)为应用文献[15]中算法的节点分布情况,该算法不仅考虑到了区域的边界条件而且重新定义了节点的邻接关系,因此提高了一定的覆盖率。图3(d)为应用文献[16]中算法的节点分布情况,网络覆盖率达到90%。图3(e)为应用本文IVFA-B算法的节点分布情况,节点分布变得相对均匀,网络覆盖率百分比也提高到91.3%。

表2 仿真实验参数

图3 网络覆盖图
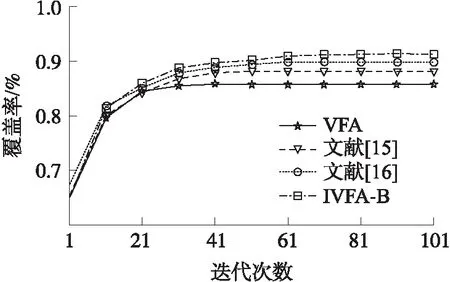
图4 覆盖率随迭代次数变化
图4表示在相同条件下分别运行VFA、文献[15-16]以及本文提出的IVFA-B算法,网络覆盖率的变化情况。在前40次迭代中,4种算法的覆盖率均有较大幅度的提高,其中IVFA-B与初始覆盖率相比提高了24个百分点,并高于其他3种算法。在40次迭代之后,IVFA-B对覆盖率的优化效果减慢,但仍有提高的空间,并逐渐趋于平稳,而其他3种算法的优化性能已经趋于平缓。
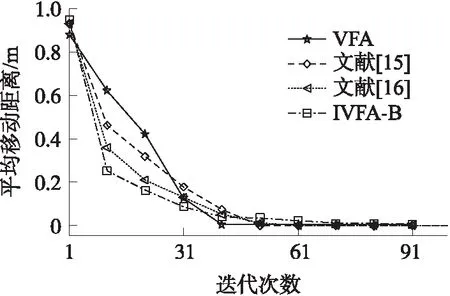
图5 平均移动距离随迭代次数变化
图5比较了随迭代次数变化,4种算法节点平均移动距离的变化情况。随着迭代次数的不断增加,节点部署情况逐渐稳定,因此节点的移动距离不断减小,但IVFA-B的减小程度始终高于其他3种虚拟力算法。
图6比较了随节点数目的变化,VFA、文献[15-16]以及IVFA-B算法网络覆盖率的变化情况。随着节点数目的增加,4种算法的覆盖率均不断增加,但IVFA-B的覆盖效果始终高于其他3种算法。当节点数目在30~45左右时,IVFA-B的优势较明显,当节点数目大于45时,覆盖率相差不大。

图8 总的移动距离随节点数目变化
由于节点能量的消耗主要集中在移动上,因此把节点的移动距离作为网络能量消耗的衡量指标。图7和图8比较了随节点数目的变化,4种算法的节点平均移动距离和总移动距离的变化情况。由于节点数目不断增加,4种算法的平均移动距离和总的移动距离均不断增加,但IVFA-B与其他3种算法相比增加的更缓慢。这是因为IVFA-B算法采用了具有一定适用性的虚拟力参数并且通过节点密集度选择最佳距离阈值,减小了节点的移动距离,在保证网络覆盖率的同时也节约了能量的消耗。
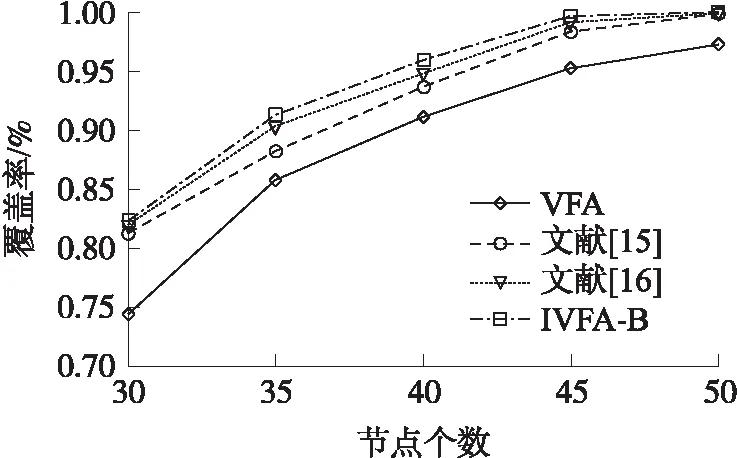
图6 覆盖率随节点数目变化
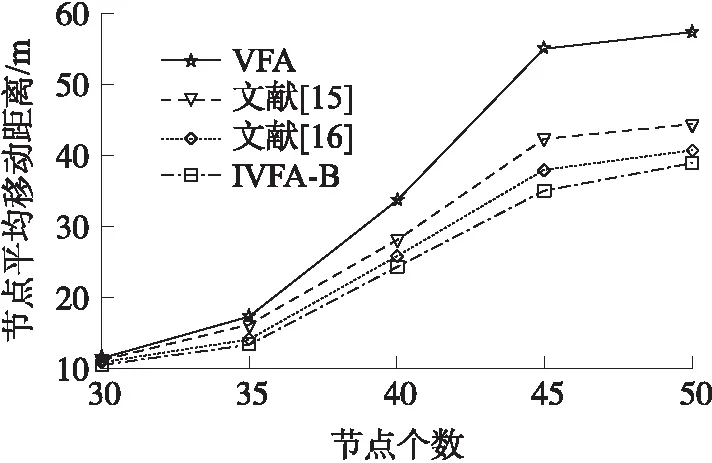
图7 平均移动距离随节点数目变化
4 总结
基于密集度的虚拟力节点部署算法在传统虚拟力节点部署算法的基础上,结合公式推导对虚拟力参数进行优化设置,弥补了在无法判断随机部署的情况下,根据经验值设置相关参数影响覆盖效果的不足。并引入节点密集度的概念,通过密集度选择虚拟力模型中调节传感器节点间的相互作用力属性的最优距离阈值,实现节点的均匀分布。通过实验验证表明,相比VFA、文献[15-16]中改进的虚拟力算法,本文所提出的部署算法在网络覆盖率和节点能耗方面具有明显的优势。今后将进一步研究有障碍物的情况下算法的适应性及相应改进策略。
