零传动滚齿机热变形的仿真分析与对齿轮加工影响研究*＊

翟文杰 刘润爱

(①太原理工大学机械工程学院，山西太原030024;②太原理工大学精密加工山西省重点实验室，山西太原030024)

滚齿是一种最为普遍高效率制齿手段之一，滚齿机不仅需要往数控化方向发展，更需要改进其内部结构［1］。传统滚齿机是由电动机带动多段传动链实现齿轮的加工，其传动速度与传动效率较为低下，无法满足现代化的高质量生产要求。为了达到高效率、大转速、低噪音的生产方式，本篇将研究一种零传动滚齿机YK3610新式机床。YK3610机床采用为卧式结构，滚刀轴转速范围为500～4 000 r/min，工件轴转速范围为5～495 r/min［2］。其机床的特点是取消了电动机与主轴之间的一切中间传动环节，把机床与主轴的传动链长度缩短为零，这种方式称为“直接驱动”或者“零传动”。优点在于减少了传动误差，提高了机床的传动效率，同时也简化了机床整体的结构。

虽然零传动滚齿机YK3610相较于传统滚齿机有很大优势，但工件轴和滚刀轴都采用电主轴形式，在运转过程中除了轴承摩擦生热，电动机的功率损耗也直接作用在主轴上，使主轴热变形误差更加明显，直接影响产品加工精度。为了进一步提高加工精度，摆脱热源对加工工件的影响，针对电主轴的发热问题进行研究具有十分重要的意义［3－4］。

1 零传动滚齿机主体结构

YK3610滚齿机的整个组成部分由滚刀轴、工件轴、进给系统、床身、数控系统和排屑系统等组成。由于滚刀存在一定的螺旋升角，因而两个主轴在空间呈交错状态进行齿轮加工。滚刀轴回转运动和工件轴回转运动均去掉一般传动滚齿机中的高精度齿轮副或蜗轮副，采用同步内置主轴电动机、同步内置力矩电动机分别驱动。内置电动机的转子与旋转轴结合为一体，通过电子齿轮箱对工件轴和滚刀轴转速进行控制［5］。图1为滚刀轴和工件轴的模型结构图。

2 零传动滚齿机热源与传热分析

2.1 零传动滚齿机热源

零传动滚齿机主要热源有4处:工件轴和滚刀轴的电动机发热;主轴支撑处的轴承发热;切削齿轮产生的切削热;机床进给机构移动处的摩擦热。工件在切削时通常会浇切削液，切削液会带走绝大部分热量，使加工质量不会受到影响。进给机构的进给速度与进给量较小，产生的热变形可以忽略。由于零传动技术采用的是电动机与主轴集成一体式的设计，主轴处的热源就变得更加集中和突出。因此如何分析主轴热源并消除其产生的影响十分关键。

2.1.1 主轴电动机发热量的计算

电动机的发热主要为铜线损耗和铁芯损耗，其中定子绕组的发热约占电动机发热总量的三分之二以上［6］。电动机发热损耗的功率Pw组成如下:

其中:Pcu为绕组损耗，W;Ph为铁芯磁滞损耗，W;Pe为铁芯涡流损耗，W。

则电动机的发热可由生热率q来衡量，其公式为:

其中:Pw为损耗功率，W;V为电动机的体积，m3。

2.1.2 主轴轴承发热量的计算

轴承运转时滚动体与滚道的摩擦产生热量，可通过摩擦力矩来衡量［7－8］，其发热量公式为:

其中:Qf为轴承发热量，W;n为轴承转速，r/min;M为摩擦力矩，N·mm。

轴承的摩擦力矩又包括外载荷施加的力矩M1与润滑液摩擦的力矩M2。外载荷施加的力矩M1计算公式为:

其中:f1为与轴承结构和载荷有关的系数;Fβ为取决于作用力大小和方向，N;dm为轴承平均直径，mm。

润滑液摩擦的力矩M2计算公式为:

其中:v0为润滑液的运动粘度，mm2/s;f0为与轴承类型和润滑方式有关的系数。

轴承的生热率为:

其中:qf为轴承的生热率，W/m3;Vb为轴承体积，m3。

2.2 零传动滚齿机传热分析

热传递的方式有3种:热传导、热对流和热辐射。滚齿机内热辐射传递量较小，热传导和热对流占主要因素。机床各类零件之间热量传递为热传导，在有限元中通过设置导热系数和接触热阻可模拟热传导形式。零件与外界流体的散热方式为热对流，在有限元中可设置边界条件来模拟，在这之前需先获取几处散热的数值。主轴内部散热途径有以下几种。

2.2.1 定子壳体与冷却水之间的对流换热

电主轴在定子外缘设有沟槽，沟槽内通入循环冷却水能吸收并带走定子产生的热量。电主轴在稳定工作条件下，其内部冷却水流量Qw为10 L/min，转子与冷却水对流换热系数aw为:

其中:d为流体的当量直径，m;Nuf为努赛尔常数(下标f表示采用流体平均温度);λ为当前温度水的导热系数，W/(m·℃)。

2.2.2 定子和转子与空隙处气体的热交换

定子和转子间对流换热系数aq为:

其中:Nu为努赛尔常数;λ为空气导热系数，W/(m·℃);dc为环形槽的当量直径，m。

2.2.3 转子端部与气体的对流换热

转子端部高速旋转带动周围气体流动，产生强迫对流换热，其对流换热系数ar为:

其中:n为转子端部的平均转速，r/min;d为转子端部的平均直径，m。

2.2.4 轴承内滚动体与滚道的导热

滚动体在滚道内因摩擦发热，随后与滚道接触传热，受挤压力影响，接触区域为椭圆形。其接触热阻R为:

其中:λ为半空间导热系数，W/(m·℃);a、b为接触椭圆面长短半轴，m。

2.2.5 主轴外壳与外界空气的换热

主轴外壳与空气的换热状态为自然对流状态，其传热系数as为9.7 W/(m2·℃)。

3 主轴热变形有限元仿真分析

3.1 建立模型与设定参数

由于用 ANSYS软件建模较为薄弱，本文采用CREO三维建模软件建立模型并导入ANSYS的方法。因为模型十分复杂，所以在建模过程中需要对模型进行简化，使简化后的模型既便于仿真又不影响分析结果［9］。

单元类型的选择与仿真分析的对象、分析类型有关。对于三维实体热—结构耦合分析可选用8节点SOLID70三维热实体单元，该单元可用于三维的稳态或瞬态热分析问题，在进行结构分析时，可被一个等效的结构单元(如SOLID45)所代替。材料属性则需要设定导热率、弹性模量、泊松比和热膨胀系数。

网格的划分影响模型在分析时的速度与精度，是十分重要的一环。工件轴和滚刀轴模型采用自由网格划分方式，这种方式系统会智能划分成四面体单元组成的网格模型，适合复杂不规则模型的网格划分。由于整个模型组成部分较多，各个部分大小不一，在保证准确性的条件下，分别给每个部分选择网格尺寸大小，然后逐一划分网格。整体划分完之后，需要在各接触零件之间建立接触对以建立整个模型的热传导关系。滚刀轴与工件轴模型网格划分如图2、3所示。

3.2 滚刀轴的有限元仿真分析

3.2.1 滚刀轴温度场分析

分析研究选定滚刀轴在额定转速2 500 r/min时的情况。设置主轴的温度载荷与边界条件如表1所示。

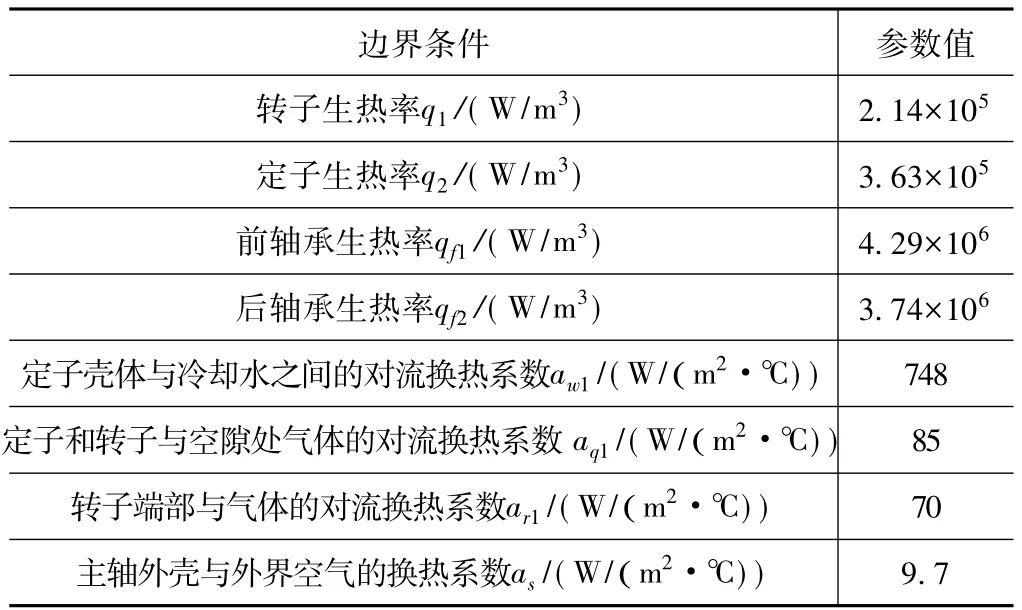
表1 滚刀轴热分析的各边界参数

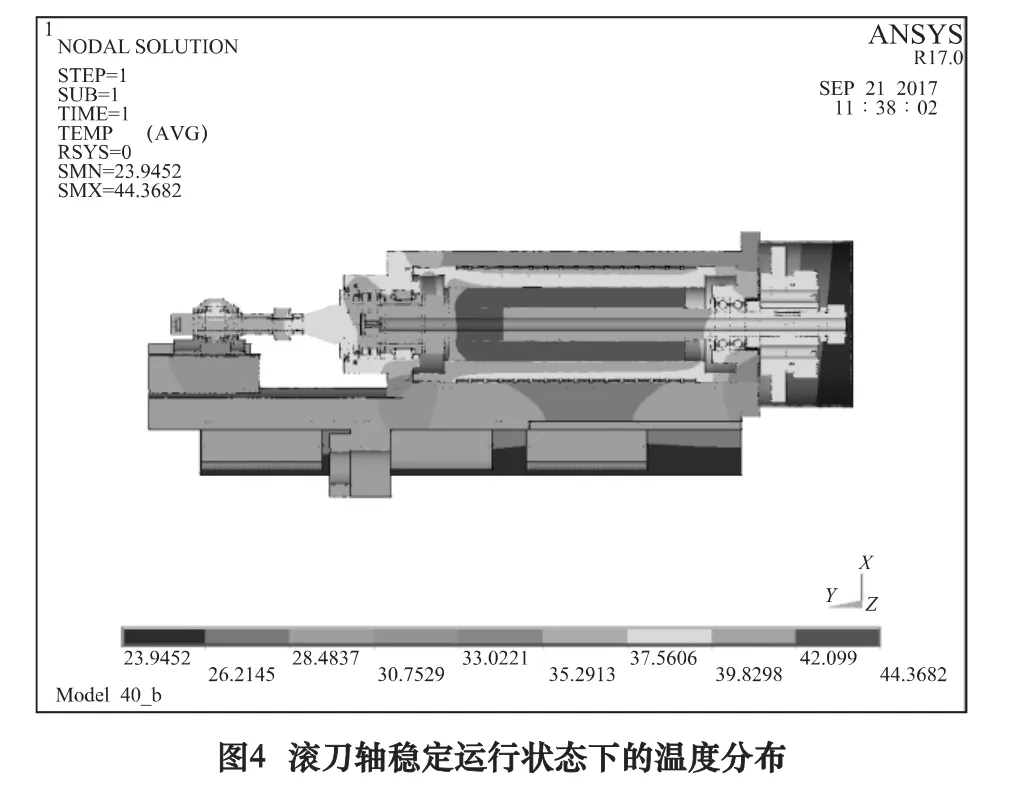
设定环境温度为20℃，求解后得到图4所示的滚刀轴稳定状态下的温度场云图。

由图4可知，在电主轴内部几处热源中转子的最高温度为44.37℃，主轴前端轴承的最高温度为42.10℃，定子端最高温度为39.83℃。造成上述现状的原因主要是转子散热较为困难，只能依靠端部与空气对流换热和与主轴进行热传导来散热。定子虽然发热是转子的一倍，但是定子外圈的冷却水却带走定子大部分的热量。轴承前端由于轴承类型和周围结构的不同温度略高于后端。

3.2.2 滚刀轴热变形分析

删除温度场分析的载荷和边界条件，将热分析转化为结构分析，然后设置温度场的数据作为结构分析的载荷，并根据实际情况施加位移边界条件［10－11］。最后求解的结果如图5、6所示。

由图5可知，滚刀轴的主轴在X向有一定量的抬升，主轴前端滚刀处的最大变形量为13.4 μm，主轴后端尾部最大变形量为6.25 μm。主要原因是主轴前端温度高于后端，因此X向的位移量也高于后端，同时尾架的发热也使主轴前端在X向上有进一步的抬升。由图6可知，主轴前端滚刀处在Y向上最大伸长量为6.36 μm，并未达到预期分析的长度，可能是因为尾架上的轴承与轴的配合间隙过小，使主轴轴向伸长受到限制，从而在X轴径向上产生弯曲变形。而Z轴方向由于滚刀轴呈对称结构，主轴的变形量十分微小，对加工质量没有影响。

3.3 工件轴的有限元仿真分析

3.3.1 工件轴温度场分析

在300 r/min转速下进行分析，其边界条件如表2所示。

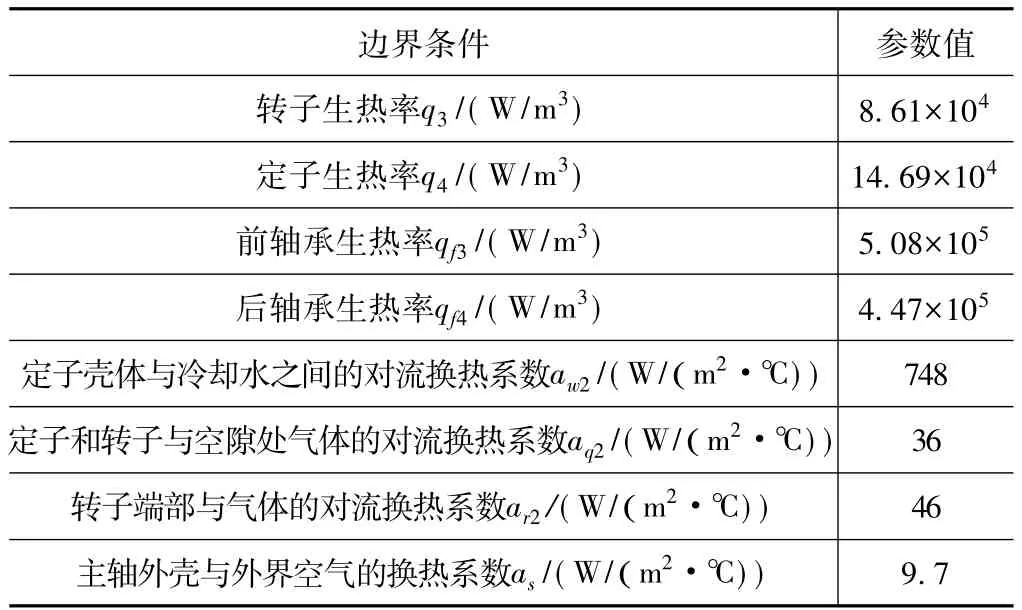
表2 工件轴热分析的各边界参数

设定环境温度为20℃，求解后得到工件轴温度场分布如图7所示。

与滚刀轴的温度分布类似，转子与主轴相连部分的温度最高，达到32.89℃;由于主轴前端轴承温度为31.62℃，后端由于编码器起到一定的散热作用，后端轴承的温度略低于前端轴承，为30.34℃，定子部分在循环冷却水的散热下温度为29.06℃。即使在室温35℃的环境下，其工作温度也远小于65℃，符合GB/T 9061金属切削机床通用技术条件的要求。

3.3.2 工件轴热变形分析

工件轴的热变形云图如图8、9所示。

由图8可知，工件轴主轴自身并无明显变形，由于底座的抬高使主轴轴头处在Y向上整体提升了6.38 μm。而工件轴前端壳体径向上较大变形是由于前端轴承安装时轴向游隙过小所致。图9中轴向最大位移量在与活塞杆相连的端盖上，由于活塞杆在主轴内部受热较多且无法散热，使活塞杆在轴向上产生较大变形，但对工件加工质量并无影响。主轴轴头在Z向上整体伸长量为43.4 μm，对工件加工有一定量的影响，需要对其进行补偿。

4 主轴热变形对滚齿加工精度的影响

主轴前端用于安装滚刀和工件，其变形量会使滚刀和工件在相对位置上产生偏差，影响工件加工精度。根据图10与图11，此机床由热变形产生的滚齿加工误差在不同方向上有以下几类:(1)径向误差。主轴在X方向上的变形引起齿轮径向误差，影响被加工齿轮齿厚与齿顶高的大小。(2)切向误差。主轴在Y方向上变形使工件相对于滚刀偏离原始对中位置而在切向上有偏移，造成工件单个齿距偏差fpt以及齿距累积偏差Fpt。(3)轴向误差。轴向误差使工件相对滚刀在Z轴产生偏差，对于加工直齿圆柱齿轮而言并无影响，但在加工斜齿圆柱齿轮时也会产生齿距偏差。

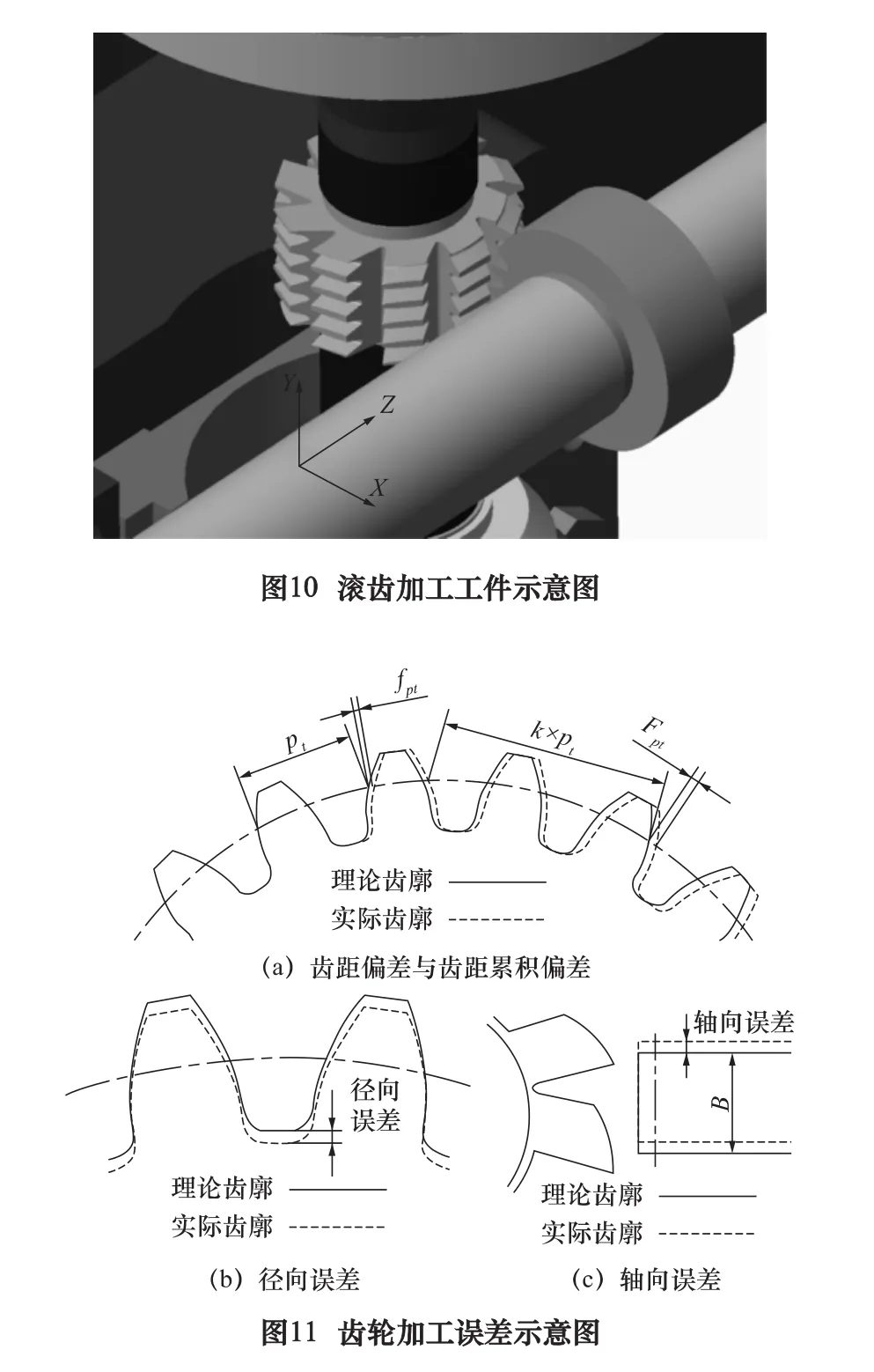
滚刀轴与工件轴在相对位置上的热变形造成刀具位置误差与工件位置误差。根据前面的仿真分析，滚刀沿X轴造成13.4 μm的齿径加工误差;滚刀与工件沿Y轴累积造成12.74 μm的切向误差;工件沿Z轴造成43.4 μm的轴向误差。对于加工高精度齿轮而言，各项误差带来的影响十分巨大，需要运用误差补偿技术进行补偿。

5 结语

本次研究运用理论计算与仿真分析相结合的方法，针对零传动滚齿机YK3610的热误差进行了模拟定量分析，得到了电动机功率损耗与轴承摩擦生热是主轴发热的主要因素，而主轴前端部的发热明显高于后端部，这使得工件连接处的变形更加明显，由此带来齿轮加工的多项误差。为了进一步提高加工精度，就需要改善主轴结构以及补偿热变形产生的误差。