基于二维网格边元设置河道方法的蓄滞洪区洪水演进分析

喻海军，吴俊峰，吴滨滨，孙宏图，马建明，高 佳

（1.中国水利水电科学研究院，北京 100038；2.水利部防洪抗旱减灾工程技术研究中心，北京 100038；3.河北省水利水电第二勘测设计研究院，河北 石家庄 050021；4.河北省防汛抗旱指挥部办公室，河北 石家庄 050011）

1 研究背景

蓄滞洪区是我国江河防洪体系中的重要组成部分，是保障重点城市和地区防洪安全，减轻洪水灾害的有效措施[1]。蓄滞洪区洪水数值模拟对蓄滞洪区洪水管理、洪水损失评估以及流域洪水调度决策等都具有重要的意义[2-4]。近年来，国内外学者在蓄滞洪区洪水数值模拟方面做了大量研究，取得了丰硕成果。王秀杰等[5]建立了河道与防洪保护区的全二维动态耦合模型，实现了宽浅河道与防洪区的无缝衔接，较好地模拟了水流流态的变化。李大鸣等[6]采用一二维耦合水动力学模型实现了大清河五洼滞洪区的实时洪水调度分析。Vorogushyn等[7]采用一维河道、溃堤和二维模型实现了溃堤洪水在蓄滞洪区内的演进模拟，对德国Elbe河蓄滞洪区内的洪灾损失进行了评估。一般来说，大型蓄滞洪区的洪水模拟一般需要构建一二维耦合模型[6-7]，但往往由于面积大、河流众多等原因导致模型时效性比较差，给实时预报分析带来一定的困难，因而十分有必要研究相对精准且高效的数值模拟方法。本文采用基于二维网格边元上设置河道的方法构建一、二维耦合模型，并选择海河流域最大的蓄滞洪区大陆泽宁晋泊蓄滞洪区为典型应用区域，对本文建立的一、二维耦合模型进行了验证与应用，并分析了下渗因素对蓄滞洪区行洪的影响。

2 模型原理

2.1 一维模型河道洪水采用一维水动力学模型模拟，控制方程为一维圣维南方程组：

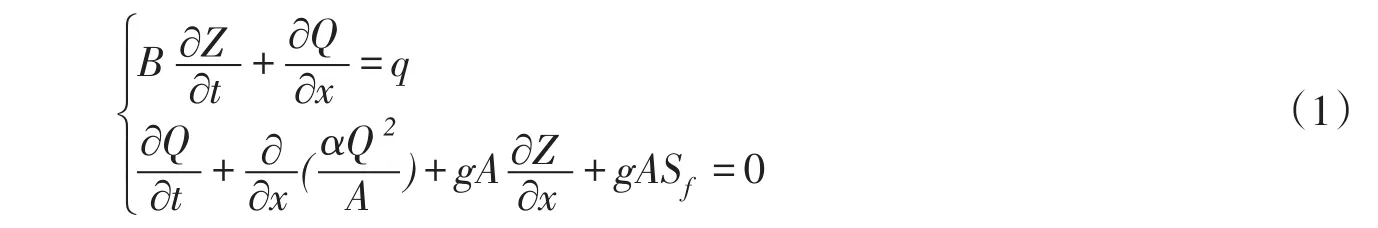
式中：q为旁侧入流；Q为流量；B为水面宽度；Z为水位；A为过水面积；α为动量校正系数；Sf为摩阻比降。

采用基于有限体积法的Godunov格式对上述一维圣维南方程组进行离散[8]。

2.2 二维模型地表洪水演进采用二维水动力学模型，控制方程采用守恒型的二维浅水方程：

式中：h、u、v、b分别为水深、x和y方向流速、底高程；Sb是底坡项；Sox、Soy分别是x和y方向的底坡比降；Sf是摩阻项；Sfx、Sfy分别是x和y方面的摩阻比降。

采用基于有限体积法的Godunov格式对上述二维浅水方程组进行离散求解，其中Riemann问题采用Roe格式的近似解进行计算，底坡源项采用特征分级离散，保证模型的守恒性，阻力源项采用隐式离散提高模型的稳定性，采用MUSCL空间重构和两步Runge-Kutta法使得模型具有时间和空间二阶精度，所有变量都定义在单元中心[9-10]。

2.3 模型耦合一维河道和二维地表水动力模型的水流交互采用边元耦合的方式（如图1所示），即在二维网格边元上设置和建立一维河网模型，网格划分时不考虑河道宽度，因而河道宽度不影响网格单元划分，可以极大的提高网格质量，从而提高模型演算效率。相对于传统分别构建一二维模型，河道范围内不划分网格或者全部采用二维模型计算，河道处进行网格加密等方法，采用边元设置河道来耦合的方式无论从网格划分便捷性还是计算效率来看都得到了极大的提升，特别适用于在计算范围内存在较多对洪水演进有影响的中小河道的情形。

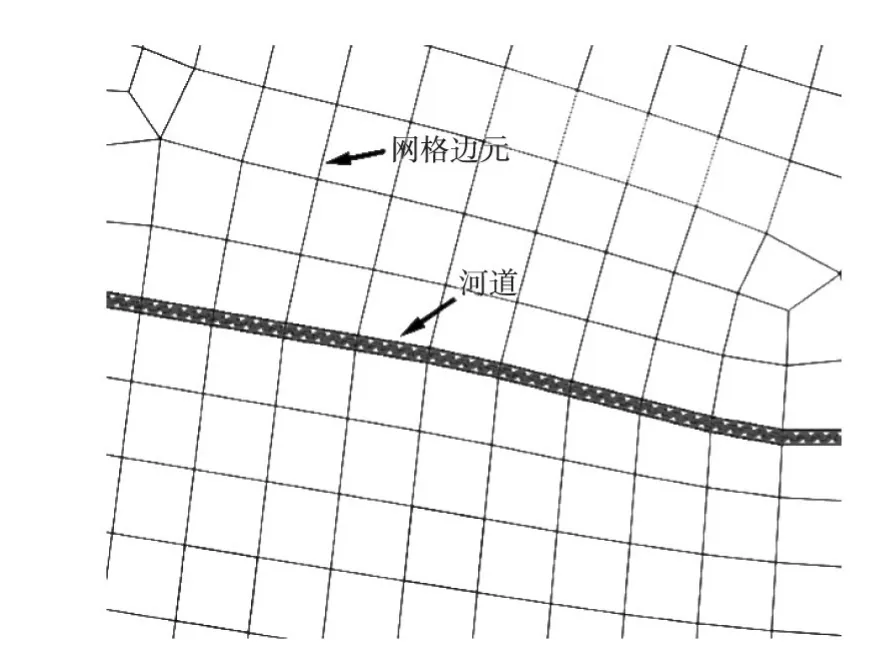
图1 二维网格边元设置河道示意

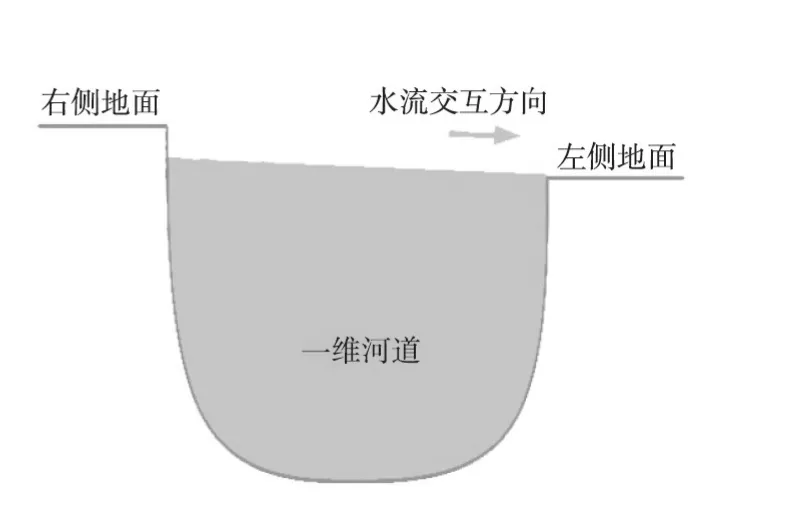
图2 河道与地面水流交互示意

如图2所示，假设某时刻河道与地表网格水量通过侧向交换的方式交换的流量为Ql，采用堰流公式近似计算交换流量的方法如下[11]：

其中：hmax和hmin分别采用下式计算：

式中：Zr、Zc分别为堰上、下游水位，分别取河道和二维网格单元的水位值；Ze为堰的高程，一般取河堤岸的高程；be为堰的宽度，一般取单元格与河道相连边的边长。

3 模型构建与应用

3.1 区域概况本文选择典型应用区域大陆泽及宁晋泊蓄滞洪区位于河北省南部（如图3所示），海河流域子牙河水系支流滏阳河系中游，河北省邢台市东北部，是全国第三大蓄滞洪区，也是海河流域第一大蓄滞洪区和关键防洪工程，总面积约2041 km2，总滞洪量35.52亿m3，涉及邢台市9个县区，135.27万人。上游河流多处于太行山迎风区，源短、坡陡、流急，洪水突发性、致灾性强。蓄滞洪区内分布有众多中小河流及堤坝，且堰闸、分区滞洪等调度规则复杂，导致一维河道与二维滞洪区洪水演进过程复杂。大陆泽、宁晋泊蓄滞洪区按50年一遇洪水设计，从建国后至今60多年的蓄滞洪区运用情况来看，大陆泽实际运用4次，最高蓄洪水位33.41 m，最大蓄洪水量10.40亿m3，蓄洪历时57 d；宁晋泊实际运用3次，最高蓄洪水位30.70 m，最大蓄洪水量29.27亿m3，蓄洪历时60 d。

3.2 模型构建

（1）网格划分。采用非结构四边形网格对整个研究区域进行网格剖分，将区域内高速公路、铁路和河流作为内部约束边界，最终共划分成约两万个网格。在网格插值时，将堤防、高速公路、铁路设置成线形阻水建筑物在网格边元上予以考虑，将测量的实际高程作为阻水建筑物的高度，采用堰流公式计算建筑物两侧的过流水量。河道糙率取0.025，其它区域糙率取值范围在0.040～0.050之间。基于网格边元设置的河道分布如图4（a）所示，网格局部放大如图4（b）所示。

图3 大陆泽宁晋泊蓄滞洪区位置示意

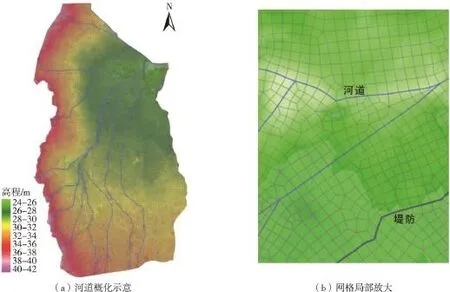
图4 研究区域网格示意

（2）边界条件。研究区域内一共包含滏阳河、留垒河、洺河、南澧河、顺水河（七里河）、牛尾河、马河（白马河、小马河和李阳河）、泜河、午河（泲河）、北沙河（槐河）、小漳河和洨河等12条中小河道。在实际模拟计算时，河道上游入流采用流量边界条件（典型洪水过程如图5所示），下游艾辛庄枢纽的出流采用水位流量关系边界（如图6所示）。

（3）分区滞洪。大陆泽及宁晋泊蓄滞洪区被滏阳河右堤和小漳河右堤划成3个分区（如图7所示），在实际调度运行中，当分区1的水位达到29.4 m时，由小南堤分洪口门向分区二分洪，当分区二的水位超过29.4 m时由小漳河右堤分洪口门向分区三分洪。模型构建时考虑了蓄滞洪区分区滞洪的调度规则，两个分洪口门则采用溃口的方式进行概化考虑，达到设定的条件（h＞29.4 m），自动进行分洪。

图5 典型洪水过程（洺河20年和50年一遇设计洪水过程）

图6 艾辛庄枢纽水位流量关系

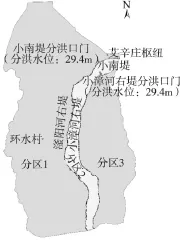
图7 分区滞洪示意

（4）模型验证。由于缺乏蓄滞洪区运用的实测数据，无法对构建的模型进行较为准确的率定验证，因而将模型计算结果与《子牙河系防洪规划》（2008年）以及《大陆泽、宁晋泊蓄滞洪区建设与管理可行性研究报告》（2014年）中的模拟结果进行比对分析，以对模型结果合理性进行检验。现状条件下，计算50年一遇洪水，采用位于蓄滞洪区上游的环水村（位于邢台市任县）以及下游艾辛庄两处（位置示意见图7）的最高洪水位进行对比，结果如表1所示。总体上，本次构建的模型与其它研究结果有一定差别，但水位差总体控制在0.15 m以内，表明模型结果是可信的，差别主要来源可能是模型算法和概化方法不完全一样。

3.3 模型应用大陆泽及宁晋泊蓄滞洪区位于海河流域，属于干旱半干旱地区，近几十年由于地下水长期处于超采状态，地下水位持续下降，导致河道和地表行洪时下渗比较强烈，对洪水演进（如洪峰、洪水淹没时间等）有着重要的影响。由于以往针对大陆泽及宁晋泊蓄滞洪区的研究成果多没有考虑下渗的影响[3]，从洪水调度管理的角度来看，不考虑下渗属于偏安全的做法，存在一定的合理性，但由于蓄滞洪区一旦启用，蓄水时间长，下渗量就相对比较大，其影响不应被忽略。本文着重对比分析了考虑和不考虑下渗情况下，蓄滞洪区洪水演进情况的区别，下渗率取值参考程亮等[12]在海河流域的研究成果，稳定下渗率取值12.3 mm/h。

图8给出了考虑和不考虑下渗两种情况下遭遇50年一遇洪水淹没范围。从图8中可以看出，在t=50 h时上下游已经有部分洪水从河道中溢出，但此时淹没深度均较小，随着时间增长，淹没范围逐渐增大。总体上看，不考虑下渗时，50年一遇洪水需要启用全部的三个分洪区，而考虑下渗时则只需启用第一个分洪区，差别比较明显。分析同一时刻考虑和不考虑下渗两种情况，可以明显看出同一时刻不考虑下渗淹没范围和淹没深度均大于考虑下渗时，而考虑长历时洪水下渗对洪水淹没范围和淹没深度都有较大影响。

表1 模拟结果对比

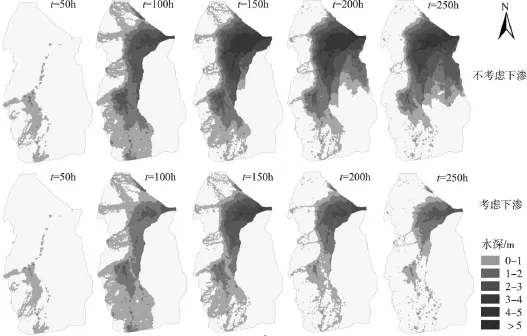
图8 50年一遇不同时刻淹没图

图9给出了20年一遇和50年一遇环水村附近洪水位变化过程。从图9可以看出，考虑下渗时的洪峰值明显小于不考虑下渗时，数值上分别减少了0.42 m和0.41 m，另外，考虑下渗时的退水时间与不考虑下渗时相比分别减少了195 h和296 h。从整个蓄滞洪区来看，以遭遇50年一遇洪水为例，不考虑下渗时蓄滞洪区需要约60 d的时间将洪水基本排尽，考虑下渗时，则只需要约36 d时间，减少了近24 d时间。

图9 环水村洪水变化过程

4 结论

（1）基于在二维边元设置河道方法，建立了大陆泽及宁晋泊蓄滞洪区一二维耦合的地表和河道洪水数值模型，在与其它模型计算结果进行对比验证时，水位差总体控制在0.15 m以内，表明该模型结果是可信的，在此基础上对20年一遇和50年一遇洪水进行了模拟与分析。应用结果表明基于二维边元设置河道的一二维耦合模型能够很好的应用于中小河流较多的蓄滞洪区，具有广阔的应用前景。

（2）对比分析地表下渗对蓄滞洪区洪水的影响可见：考虑下渗作用时，蓄滞洪区50年一遇洪水只需要启用1个分区，而不考虑时则需要启用3个；考虑下渗时退水时间与不考虑下渗时相比也相应减少了近24 d。表明干旱半干旱地区下渗对蓄滞洪区行洪具有较大的影响，在蓄滞洪区实际调度应用时，应该考虑下渗因素对洪量减少的影响，以较好发挥蓄滞洪区的效用。