通过一道题将知识连成片、串成串

北京 公衍录

通过对一道题的多求、多变等，将相关的知识点连成片、串成串，形成知识结构，这无疑是习题教学中比较好的做法，下面以2016全国卷Ⅱ第23题为例加以说明。

【题目】如图1，水平面(纸面)内间距为l的平行金属导轨间接一电阻，质量为m、长度为l的金属杆ab置于导轨上。t=0时，金属杆在水平向右、大小为F的恒定拉力作用下由静止开始运动，t0时刻，金属杆进入磁感应强度大小为B、方向垂直于纸面向里的匀强磁场区域，且在磁场中恰好能保持匀速运动。杆与导轨的电阻均忽略不计，两者始终保持垂直且接触良好，两者之间的动摩擦因数为μ。重力加速度大小为g。求：

(1)金属杆在磁场中运动时产生的电动势的大小；

(2)电阻的阻值。

【解析】(1)如图2，在0～t0时间内，对金属杆受力分析，

根据牛顿第二定律得：F-μmg=ma①

设杆进入磁场瞬间的速度为v，则v=at0②

由法拉第电磁感应定律可知，E=Blv③

(2)杆进入磁场后，还受水平向左的安培力F安=BIl⑤

由杆在磁场中做匀速直线运动可知，

F-μmg-F安=0 ⑥

【点评】本题考查了共点力的平衡条件、牛顿第二定律、匀变速直线运动等力学知识在电磁感应问题中的应用。

杆在磁场中的匀速运动是一种典型的物理模型，下面借助此模型对该题进行一题多求、一题多变的拓展变化。

一、一题多连

1.在原题中，当杆进入磁场以速度v匀速时，试证明在一段时间t内，恒定拉力F对杆做的功W等于电路获得的电能E电，也等于回路中产生的焦耳热Q。

【证明】杆匀速，受力平衡，拉力F=F安，因此拉力F对杆所做的功W等于杆克服安培力做的功，即W=F安x，又F安=BIl，x=vt，电动势E=Blv，电荷量q=It，故W=BIlvt=EIt=Eq;

由焦耳定律Q=I2Rt，闭合电路的欧姆定律E=IR，电荷量q=It，故Q=EIt=Eq。

所以在一段时间t内，恒定拉力F对杆做的功W等于电路获得的电能E电，也等于回路中产生的焦耳热Q。

2.试用多种方法推导杆中产生的感应电动势大小E=Blv，式中v为杆进入磁场做匀速运动的速度。

【推导】方法一：由法拉第电磁感应定律推导

方法二：利用电动势的概念推导

方法三：由杆中自由电子受力平衡推导

杆作为电源，由于其电阻忽略不计(内电阻为零)，内电压为零，故杆两端电压(路端电压)U等于电动势E，因此电动势为E=U=Blv。

方法四：由功能关系推导

通过拉力克服安培力做功将其他形式的能转化为电能，又通过电流做功将电能转化为内能。故拉力克服安培力做功的功率，等于电路中电流做功的功率，即P克安=P电，又P克安=F安v=BIlv，P电=EI，联立解得：E=Blv。

或由纯电阻电路，拉力克服安培力做功的功率，等于电路中的电热功率，即P克安=P热，又P克安=BIlv，P热=I2(R+r)，E=I(R+r)，联立解得：E=Blv。

或由拉力克服安培力做的功，等于杆(电源)中非静电力做的功，即W拉=W非，又W拉=BIlx，x=vt，电荷量q=It，W非=qE，联立解得：E=Blv。

3.推导电流的微观表达式。

设杆中单位体积内有n个自由电子，杆中所有自由电子均以速度ve相对杆做匀速直线运动。杆的横截面积为S，电子的电荷量为e，试推导杆中电流的微观表达式为I=nveSe。

4.试证明杆受的安培力F安，等于杆中所有自由电子受水平向左洛伦兹力分力的总和f总。

【证明】电子以速率ve相对杆由a向b定向移动，由左手定则，每个电子受水平向左、大小为fx=eveB的洛伦兹力分力，杆内总电子数N=nSl，所有电子受水平向左洛伦兹分力的总和f总=Nfx，又I=nveSe，联立解得f总=BIl。又杆在磁场中匀速运动时，受水平向左的安培力，F安=BIl，故f总=F安,得证。

5.试证明洛伦兹力不做功。

【证明】杆中电子受水平向左的洛伦兹力分力fx=eveB，其做功功率为Px=-fxv=-eveBv；杆中电子受沿杆的洛伦兹力分力fy=evB，其做功功率为Py=fyve=evBve，所以Px+Py=0，即洛伦兹力的两个分力做功功率之和为零，故洛伦兹力不做功。

二、一题多变

【变式1】原题中，如果在杆匀速运动的某一时刻、突然将拉力F撤去，经过时间t杆停止运动，则在从撤去拉力到杆停止运动的过程中:

(1)杆的加速度的大小如何变化？

(2)流过回路某一横截面的电荷量是多少？

(3)杆运动的位移大小是多少？

(4)安培力对杆所做的功是多少？产生的焦耳热、摩擦生热各是多少？

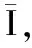
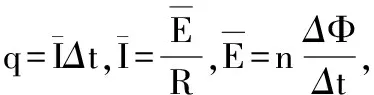
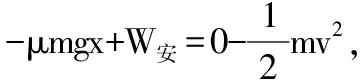
【变式2】杆进入磁场后，若在回路中磁感线穿过的面积为S时记作t=0时刻，从此时刻起，让磁感应强度逐渐减少，则磁感应强度Bt应怎样随时间t变化(写出Bt与t的关系式)，才能使回路中不产生感应电流？

【解析】解法一：从功的角度求解

解法二：从功率的角度求解

解法三：从力的平衡角度求解之一

如图4所示，因为杆以速度v水平向右运动，电子受到洛伦兹力沿杆方向的分力fy作用，方向由a端指向端b，大小fy=evB。

沿杆方向，电子还受到杆两端电压(路端电压)形成的电场给的电场力作用，方向由b端指向a端，