混合矩阵的二次特征值反问题及其最佳逼近

周 硕，杨 帆

(东北电力大学 理学院，吉林 吉林 132012)

矩阵反问题在诸多领域都有重要应用[1～5].近年来，二次特征值反问题的研究十分活跃，尤其是对特殊结构矩阵的研究[6～12]，更多合理的解决方案不断提出[13～16].本文主要研究一类二次特征值反问题的对称正交反对称解和对称正交对称解.

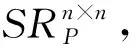
本文提出并解决如下两个问题：

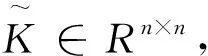
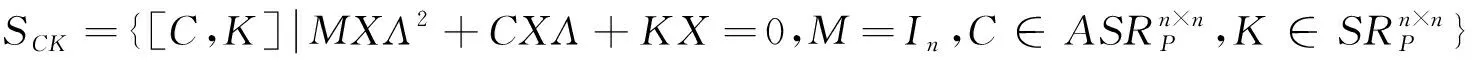
1 问题I的解

设P是n阶对称正交矩阵，则存在n阶正交矩阵U，使

(1)

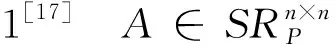
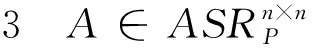
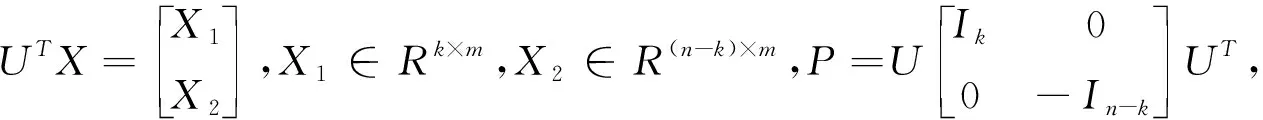
由此可得

X1Λ2+C1X1Λ+K1X1=0

，

(2)

X2Λ2+C2X2Λ+K2X2=0

，

(3)

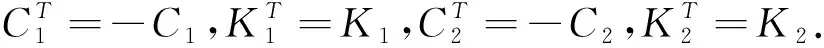
将公式(2)、公式(3)两端同时取转置，记为公式(4)和公式(5)

(4)

(5)

将原问题转化为如下两个矩阵方程组的求解问题

(6)

(7)

由矩阵的Kronecker乘积，方程组(6)等价于如下矩阵方程

(8)

方程组(7)等价于如下矩阵方程

(9)

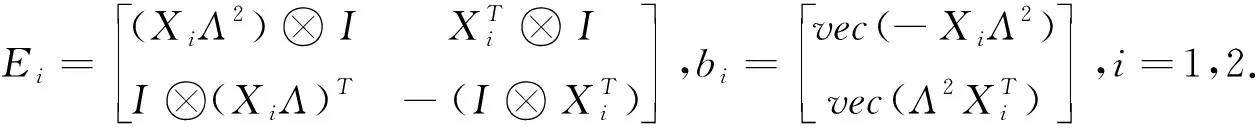
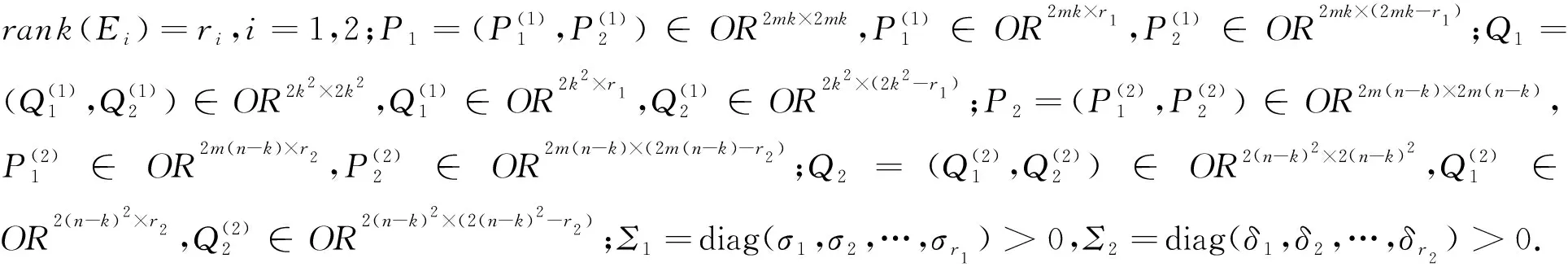
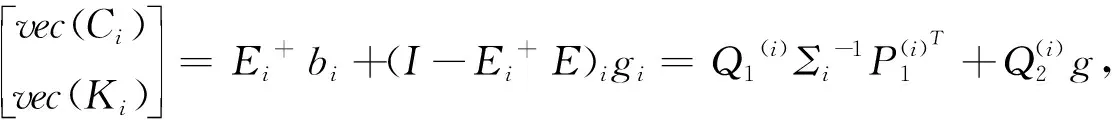
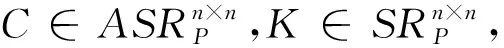
其中：

C1=[x(1：k)，x(k+1：2k)，，x((k-1)k+1，k2)]，

K1=[x(k2+1：k(k+1))，，x((2k-1)k+1：2k)]，

C2=[y(1：n-k)，y(n-k+1：2(n-k))，，y((n-k-1)(n-k)+1)：(n-k)2]，

K2=[y((n-k)2+1：(n-k+1)(n-k))，，y((2(n-k)-1)(n-k)+1：2(n-k)2)].

2 问题Ⅱ的解

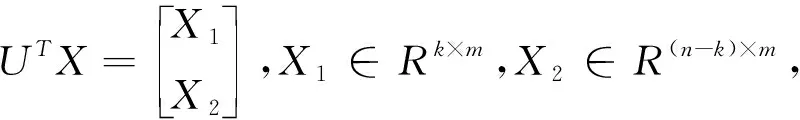
其中：Γ1=diag(Ξ1，In-k-r1)，Γ2=diag(Ξ2，Ik-r2)，

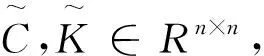
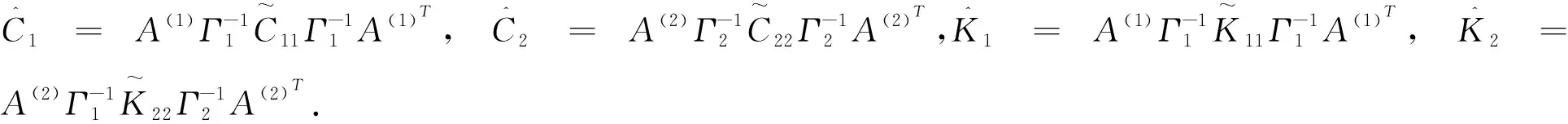
证明

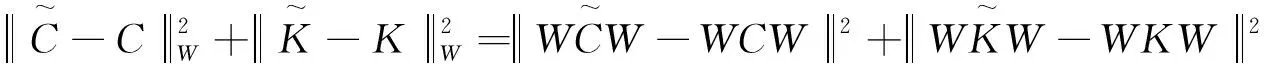
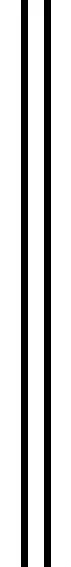
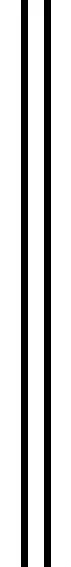
的充分必条件是

同时成立.