基于ANFIS的光伏输出功率超短期预测方法研究

杨 茂，黄 鑫，苏 欣

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.东北电力大学 理学院，吉林 吉林 132012)

光伏发电已成为继风力发电后可再生能源发电的又一新增长点.2009年～2013年，中国光伏发电的装机容量以平均每年超过1倍的速度增长.2014年我国装机容量已达到28 GW，仅次于德国的38.2 GW，位居世界第二[1].2015年底，我国以43.18 GW光伏发电装机容量跻身为世界上光伏发电装机容量最大的国家[2].截至2016年底，我国累计装机容量77.42 GW，光伏发电新增装机容量为34.54 GW，新增和累计装机容量均位列全球光伏产业的首位[3].

光伏功率受光照强度、湿度、电池板温度等因素影响，具有较大的随机性和波动性.这种随机性和波动性导致光伏发电在大规模并网时对电网造成一定的不良影响.因此，准确的光伏功率预测对于电力系统的安全经济运行具有重要意义.

图1 不同天气类型下光伏输出功率日曲线图

光伏功率预测，即根据历史数据，通过一定的建模方法，对未来一段时间的光伏功率进行预测[4].文献[5]利用BP(Back Propagation)神经网络进行短期光伏功率预测，将湿度、气温作为输入量，根据自组织特征映射进行天气聚类识别，算法容易陷入局部最优问题.文献[6]建立反向传播神经网络的无辐照度光伏功率短期预测模型，分析光伏发电量与气象因素的相关性，采用自组织特征映射对天气类型聚类识别，利用云量进行自适应特征映射天气类型聚类识别，预测精度有所提高，但算法复杂度过高，运算时间长.文献[7]建立基于相似日、支持向量机和持续法的组合预测模型，根据粗糙集理论决定属性重要度的方法确定单一预测模型的组合权重，以日为单位确定权重值并不合理.文献[8]对传统灰色BP神经网络模型的光伏预测方法进行了改进，一定程度上提高了预测精度.文献[9]提出一种基于滚动的自回归积分滑动平滑模型(ARIMA)和支持向量机(SVM)相结合的卡尔曼融合预测模型，提高了预测精度.文献[10]将优化支持向量机(SVM)、人工分群算法(ABC)以及经验模态分解(EMD)有效地结合起来构成了光伏并网系统输出功率预测模型，该方法较单一预测方法具有一定的优势，在预测精度以及运算速度上有进一步地提高.

本文考虑气候的复杂变化，将天气划分为晴天、多云、阴天和雨天4种类型，每隔15 min预测一次之后四小时的天气类型，在各天气类型下构建特定的基于ANFIS模型的光伏功率超短期预测模型.在构建模糊推理结构时，采用减法聚类算法，此算法不需人为设定，有效避免在构建结构时的盲目性和主观性.最后利用吉林省某高校光伏实验室实测数据进行实验，结果验证了本文方法的有效性.

1 光伏功率输出特性分析

在不同天气类型下典型的光伏发电输出功率曲线，如图1所示.从图中可以看出，在晴天和雨天的情况下，光伏功率波动较小；在多云和阴天的情况下，光伏功率波动较大.不同天气类型下，光伏功率输出的差异性较大，为提高光伏功率预测精度，本文将在不同天气类型下对光伏输出功率进行超短期预测.

2 多步滚动实时预测模式

进行光伏功率超短期预测时，需进行多步滚动预测模式[10]：

，

(1)

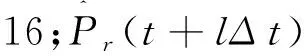
根据国家能源局就光伏发电功率预测系统功能规范的有关规定[11]，超短期光伏功率预测应每15 min自动上报一次，上报时间为未来15分钟至4小时的光伏功率预测数据.

3 ANFIS预测模型

ANFIS模型，结合了神经网络模型和模糊推理系统.其实质是由Takagi等提出的一组基于语言规则推理模型.在进行模糊推理系统推理时，需通过一系列的映射.在研究这些映射过程时，隶属度函数的选取通常是通过以往经验直接选取的，这样导致模糊推理系统的模糊规则具有一定的随机性和主观性，这显然是不合理的.

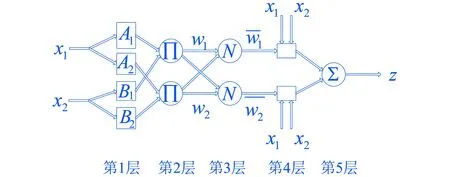
图2 ANFIS模型结构(2个输入)

对于神经网络而言，其最大的优点是自组织学习能力.ANFIS系统即能弥补传统模糊推理系统的缺点，又可阻止人工神经网络在运行时造成局部最优的问题.假设ANFIS模型的输入数为2，则其结构如图2所示[12].

图中，设Ok，i表示为第k层的第i个节点的输出.

第1层：各节点i都由节点函数表示(参数具有可变性)如下：

(2)

式中：x1、x2为节点i的输入量；Ai(或Bi-2)为与该节点函数值有关的信息量；A(A=A1，A2，B1，B2)为模糊集；O1，i表示隶属度函数，选择高斯函数作为隶属度函数.

第2层：该层节点为图2中的Π，wi为模糊规则激励强度：

O2，i=wi=μAi(x1)μBi(x2)，i=1，2

.

(3)

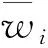
(4)

第4层：该层各节点均为自适应节点，对每条规则的贡献进行计算，输出结果为

(5)

式中：pi、qi以及ri均为结论参数.

第5层：对所有规则的最终输出进行计算，即计算总输出为：

(6)

本文采用减法聚类算法形成模糊推理系统结构，该结构能够对重复优化过程的模糊辨识方法和模糊聚类进行初始化，聚类所形成的规则也相对于人工设定结构所得到的模糊规则更加符合数据之间对应关系[13].

4 超短期光伏功率输出预测评价指标

本文采用的误差评价指标是国家能源局就光伏发电功率预测系统功能规范中提出的[11].

日平均预测合格率计算模型如下：

(7)

(8)

式中：r2i为第i次光伏输出功率预测的合格率；r2为一天中预测的平均合格率.一天的光伏功率预测均方根误差为r3，其求解模型为

(9)

5 算例分析

本文数据来自吉林省某高校光伏实验室光伏测试平台，该平台装机容量为10 kW，采样时间为2015年1月1日至1月31日的上午6点到下午5点，采样间隔为15 min.

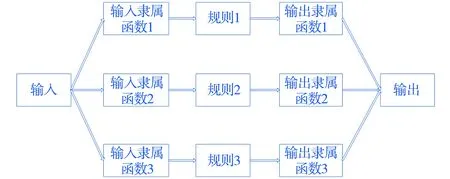
图3 ANFIS模糊系统的结构图

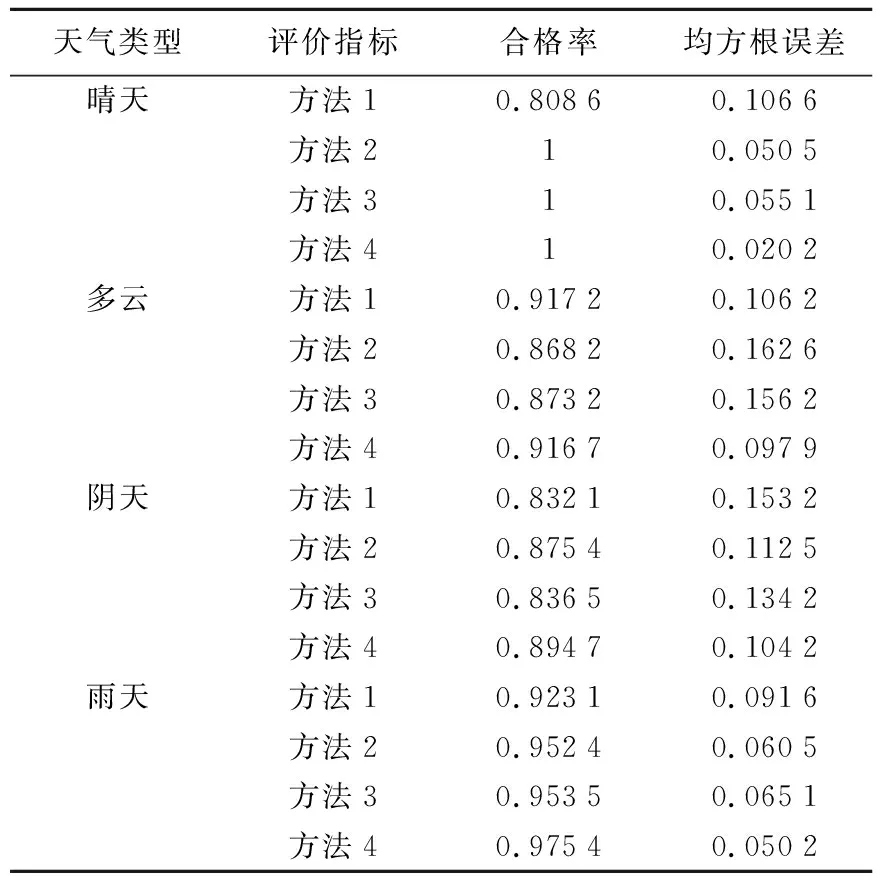
天气类型评价指标合格率均方根误差晴天方法10.80860.1066方法210.0505方法310.0551方法410.0202多云方法10.91720.1062方法20.86820.1626方法30.87320.1562方法40.91670.0979阴天方法10.83210.1532方法20.87540.1125方法30.83650.1342方法40.89470.1042雨天方法10.92310.0916方法20.95240.0605方法30.95350.0651方法40.97540.0502

不同天气类型下，利用不同光伏功率预测方法进行预测时的评价指标统计表，如表1所示.其中，将BP神经网络[14]、多尺度持续法[15]、多尺度滑动平均法[16]和ANFIS法分别记为方法1、方法2、方法3和方法4.将实测历史气象数据：辐照度、湿度、温度作为BP神经网络的输入数据.在输入各气象数据前，需对各气象数据进行归一化处理.归一化模型为

(10)

式中：x为原始数据；x′为归一化之后的数据.多尺度持续法和多尺度滑动平均法是根据光伏输出的日周期性，在原始模型的基础上，将尺度调整到以天为单位进行建模求解.

采用方法4进行光伏功率超短期预测时，参数的选取如下：隶属函数为高斯函数；隶属函数个数为3个；训练次数为2 000次；在特定天气类型下，训练样本选取光伏功率历史实际值和历史天气数据.对光伏功率利用ANFIS建模方法进行预测时，所得初始化模糊系统结构如图3所示.

由表1可知，通过ANFIS模型对光伏功率进行预测时，在不同的典型天气类型下，其准确率均高于其他预测方法，全天预测结果均方根误差也均低于其他预测方法.由于各种典型天气类型下光伏功率波动性不同，即晴天与雨天所具备的规律性较大，阴天与多云天气光伏功率具备的规律性不大，所以预测难度不同，在表1中的评价指标也有所体现，ANFIS法的预测精度要高于另外三种预测方法，说明了ANFIS预测模型的有效性.

列举晴天与多云这两种天气类型下在某日11：45时进行的预测，基于各预测方法下的预测值和真实值对比如图4所示.其中图4(a)为晴天，图4(b)为多云天气.在预测中，ANFIS预测模型的预测结果最接近真实值.

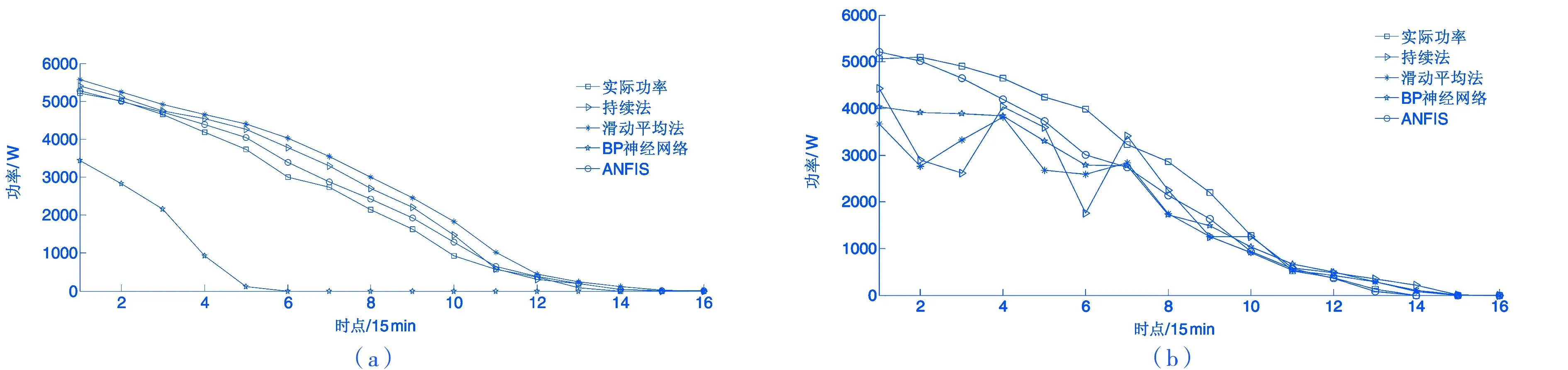
图4 各模型预测结果(某日12：00到15：00)

6 结 论

本文分析了光伏功率预测中超短期多步滚动预测模式，并提出了基于ANFIS的预测模型，由减法聚类形成初始模糊系统结构，有效地避免了人工设定结构法有可能产生组合爆炸的问题.通过天气预报确定待预测日的天气类型，将天气类型划分为晴天、多云、阴天和雨天，分别进行建模预测.算例结果表明，在不同天气类型下，本文所提出的ANFIS预测模型在进行超短期光伏功率预测时，在晴天和雨天天气下均方根误差能在5%左右，在多云以及阴天天气下均方根误差在10%左右，预测精度较传统预测方法均方根误差平均下降5%左右，验证了本文方法的有效性.