低渗压裂气井产能预测方法研究与应用

高 杰，冯 青，秦俊杰，汪 超

（中海油田服务股份有限公司油田生产研究院，天津 300459）

产能预测是评价油气层生产能力的重要指标，准确合理地预测产能，是目前面临的一项技术难题。关于低渗气藏[1-3]压裂井产能预测的方法[4-9]较多，主要有汪永利等[8]应用保角变换原理，将垂直裂缝的气井产量问题转化为单向的渗流问题，可用于描述井筒附近较复杂的渗流型态对压裂后产能的贡献，熊健等[9]考虑气体渗流特征受到启动压力梯度、滑脱效应、应力敏感等因素影响，基于非达西理论，用于保角变换方法，推导了考虑气体上述因素共同作用下的低渗气藏无限导流垂直裂缝井产能方程。这些模型大多集中在预测模型的推导及修正，但往往忽略了气层参数选取不合理引起的产能误差。在诸多气层参数中，地层系数[10，11]是最能反映储层物性好坏、生产能力强弱的，因此合理的选取气层厚度及渗透率是极其重要的。本文提出岩心归位校正气层厚度及渗透率，划分渗透率级差范围，有效排除非产能贡献层对产能预测的干扰。同时建立地层系数、采气指数与渗透率级差的关系图版，优选最佳的渗透率级差范围。

笔者在前人研究水平井模型[12，13]的基础上，只考虑单条裂缝的影响，建立考虑裂缝内渗流阻力及压力损失的压裂直井产能预测模型。对该模型采用岩心归位校正的参数，观察不同渗透率级差范围内的产能预测结果与测试结果在产量上的相关性，对比汪永利、熊健产能预测模型结果，结合实例分析，验证该方法的可靠性。

1 气层厚度和渗透率的校正方法

1.1 A气田储层特征

A气田属于低渗（致密）气藏。岩心物性分析资料表明，储层孔隙度在 5%～10%、渗透率小于（0.1～1）×10-3μm2所占比例分别为64.14%和55.56%，属于低孔渗储层特征。砂岩储层段厚度较大，最大的厚度高达96 m，纵向上以发育若干正粒序沉积组合为特征。单个正粒序沉积底部常见砂砾岩，向上过渡为含砾粗砂岩、中、细砂岩、含毫米级泥质纹层的粉砂岩或泥质粉砂岩到正常湖相沉积泥岩。岩性及碎屑岩颗粒粒度的快速变化造成储层垂向渗透率具备较强的非均质性。工作区压裂测试井气层非均质性统计表（见表1），渗透率级差大于5的占50%，最大的渗透率级差为943.64。

表1 A气田已压裂井储层非均质性参数统计表

1.2 气层厚度和渗透率的校正方法

前人研究表明[14，15]，受渗流启动压力影响，在测试、投产初期气层内渗透率低到一定程度，不足以克服气体启动压力条件，对压后产能没有贡献。由于本区气层非均质性较强，在进行压后产能预测时，需要考虑对产能有贡献的气层渗透率界限及气层的有效厚度。

基于以上原因，本文提出岩心归位校正气层厚度和渗透率，划分渗透率级差范围，可以合理地筛选有效气层段。

1.2.1 不同级差范围内的气层厚度和渗透率 以井12为例，岩心归位后将该井的岩心密度与岩心渗透率进行交会（见图1），回归后的公式为y=3E+23e-22.07x，将测井解释的气层段对应的密度代入该公式，计算气层不同深度点渗透率，用最大渗透率除以每个点的渗透率，得到各个点的渗透率级差。根据级差值，划分小于5、8、10、12、15 共计 5 个范围，计算对应范围内的气层厚度及渗透率加权平均值。

基于上述方法，得到A气田压裂气井不同渗透率级差范围内对应的气层厚度及渗透率加权平均值。级差范围越大，厚度越大，渗透率越小（见表2）；级差范围越小，厚度越小，渗透率越大。通过该种方法可以确定对产能有贡献的气层渗透率及气层的有效厚度界限。

图1 井12岩心密度与岩心渗透率交会图

表2 不同级差范围内的气层厚度及渗透率

1.2.2 确定对产能有贡献的渗透率级差 地层系数的大小代表着气层生产能力的大小，通过分析A气田压裂测试井不同级差范围与地层系数之间的相关性（见图2），可以判定该区域最佳的级差范围。

由图2可知，可将该区域的井分成2种情况。即：井7、井9地层系数不随级差范围的变化而改变，说明气层均质性较好，非均质性可以忽略；其余井随着级差范围的增大，地层系数增大，曲线在初始阶段（渗透率级差小于10）上升较快，后期慢慢趋于水平，说明渗透率级差大于10对产能贡献较小，甚至可以忽略。

理论上，米采气指数和渗透率具有正相关性。在进行产能预测时，参与计算的渗透率与实际米采气指数的相关性越好，说明该渗透率越符合地层的真实情况。

渗透率与米采气指数的关系图（见图3），图3（a）为测井解释渗透率，图3（b）为岩心归位与测井校正后渗透率，图 3（b）相关性好于图 3（a），验证了校正后的渗透率更能准确的预测该区域的产能。

2 产能预测

2.1 产能预测模型

基于文献[7]的研究，只考虑单条裂缝的影响，修正量纲，推导出产能预测公式为：

式中：pe－供气边缘压力，MPa；pwf－井底流压，MPa；pSC－标准状况下的压力，MPa；T－地层温度，K；TSC－标准状况下的温度，K；k－地层渗透率，mD；h－储层厚度，m；Re－供给半径，m；Qg－气井压裂后的产量，m3/d；Xf－裂缝半长，m；kf－裂缝渗透率，mD；wf－裂缝宽度，m；rw－井筒半径，m。

图2 渗透率级差与地层系数关系曲线

图3 渗透率与采气指数的关系图

2.2 预测结果分析

2.2.1 产能预测结果对比分析 应用式（1）分别采用测井解释数据和校正后的数据，进行预测产能，与实际产能进行对比（见图4），直接采用测井数据计算的平均相对误差为91.39%，而经过校正后平均相对误差降低为26.28%，可以满足现场决策需要。

2.2.2 产能预测模型对比分析 将本文修正后的公式与汪永利、熊健模型进行对比，采用的数据均为取级差小于10对应的气层有效厚度和渗透率进行产能计算，结果（见图5）。修正模型与实际产能对比偏离最小，平均相对误差为26.28%，汪永利模型平均相对误差值为57.36%，熊健模型平均相对误差值为179.52%，两种模型不符合生产单位对产能预测的要求。

3 实例应用

某气井，地层压力43.4 MPa，地层温度156℃，计算级差小于10的气层有效厚度为44.7 m，渗透率加权平均值为0.69 mD，设计加砂量45 m3、支撑裂缝半长170.1 m、支撑裂缝宽度0.001 71 m、支撑缝高55.6 m、裂缝导流能力228.3 mD·m，压前采用修正模型预测不同压差下产能情况（见图6）。

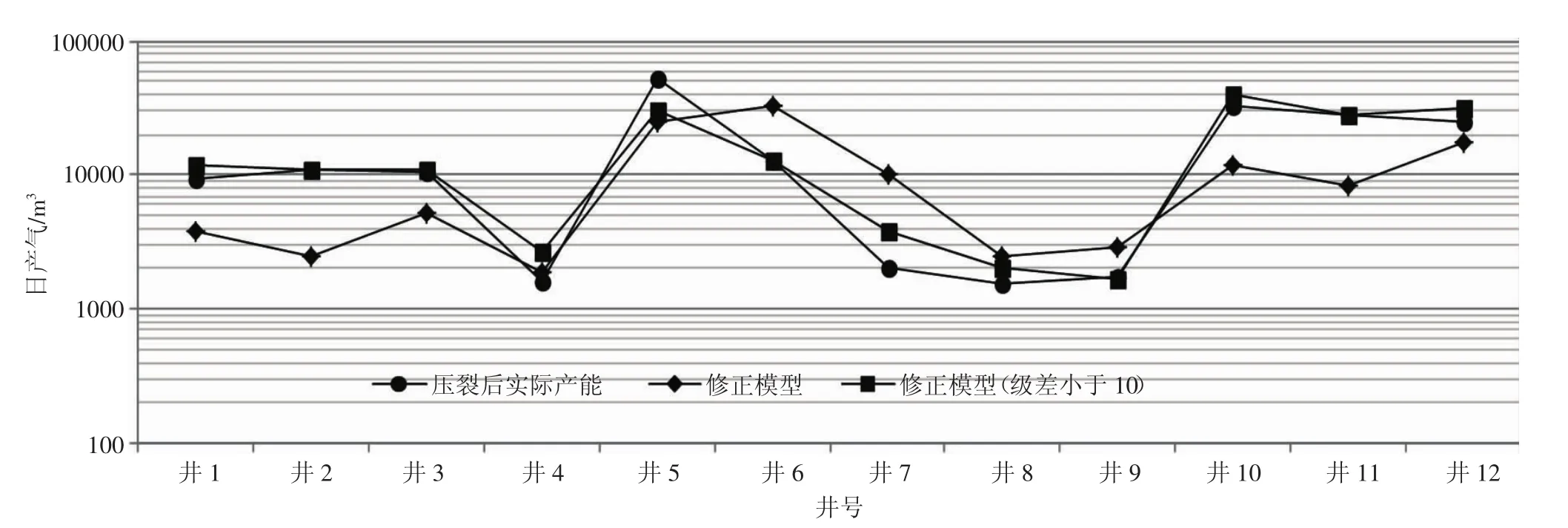
图4 预测产能与实际产能对比图

图5 产能预测模型对比

该井于2015年10月进行压裂施工，实际加砂量为44.5 m3，裂缝监测获得支撑裂缝半长为221.9 m，支撑缝高58.2 m，支撑裂缝宽度0.001 66 m，压后生产压差为7.71 MPa，获得稳定产能为4 662 m3/d，预测产能与真实产能相对误差为6%，验证了该模型预测的准确性。

4 结论

（1）本文提出岩心归位校正气层厚度及渗透率法，计算不同渗透率级差范围内的气层有效厚度及渗透率，有效的排除非产能贡献层的干扰。

（2）通过渗透率级差范围与地层系数、米采气指数的相关性分析，得到渗透率级差小于10时，是最佳贡献的渗透率级差范围，且较测井解释数据更符合实际地层情况。

（3）修正后的模型分别采用测井解释及渗透率级差小于10时数据，进行产能计算，平均相对误差分别为91.39%和26.28%，验证了该方法的符合性。

（4）将修正模型与汪永利、熊健模型的产能预测结果对比分析，平均相对误差分别为26.28%、57.36%和179.52%，说明了该模型对A气田的适应性。

（5）通过该模型、方法指导A气田某气井的压后产能预测，预测产能与实际产能相对误差为6%，进一步验证该模型及方法的可靠性。