3-RRR球面并联机构优化设计研究
2018-07-19柳伟兵赵宏宇
杨 健,周 鑫,柳伟兵,赵宏宇
(成都理工大学 核技术与自动化工程学院,四川 成都 610059)
1 引言
少自由度并联机构凭借其多角度、高灵活性、输出端误差累积效应小等优点在机械加工、航天航空、3D打印、工业机器人等领域起到串联机构不可替代的作用。其中3-RRR纯转动球面并联机构作为典型代表,在其运动空间内具有定位精度高、运动灵活性较好等特点而被广泛关注。
文献[1-2]分别对这类并联机构的构型组合方法、静力学问题进行了探讨,文献[3-6]则针对运动学、空间奇异性等问题进行了研究。但此类3-RRR纯转动球面并联机构的结构参数并不唯一,在保证9个运动副的轴线相交于空间内一点的基础上,每个运动杆件的形状、角度、动静平台的空间角度等参数各不相同,因此工程适应性各不相同。国内学者对此研究相对较少,国外有代表性的是:学者Bai.S利用空间四连杆建立对机构的约束,并通过将空间运动方程的正弦形式转化为由输入角的正切方程所构成的二项式形式,然后利用多项式的根值存在定理求解出的机构奇异位置,以进一步求解出几组合理的机构几何参数,最后利用其对应的雅克比矩阵加以验证[7-8]。但这些利用几何约束关系和空间奇异关系推导出合理结构参数,然后针对这些参数对其运动的灵巧性和工作空间进行验证的方法,存在在工作空间最大化的求解过程中,各待解参数有陷入局部最优解和漏解,甚至无法取得灵巧性最大结构参数的问题[11-13]。
提出了一种智能遗传算法,以3-RRR并联机构的雅可比矩阵条件数为优化目标,以机构中电机输入角度、各运动部件几何构型、动静平台的空间角度等为优化参数,来获取机构最大的工作空间和运动灵巧性。
2 3-RRR球面并联机构工作原理
2.1 3-RRR球面并联机构的构成模型
建立如图1所示坐标系。取第一条运动学支链A1B1C1为研究对象,即图中阴影部分,此运动链底部静平台开始至顶部动平台之间的三个运动副关节的方向矢量描述依次为:u1、w1、v1,每个关节对应的旋转角度为θ1、φ1、ψ1,矢量u1与矢量w1之间的夹角记为α1,矢量w1矢量v1之间的夹角记为α2,矢量u1与竖直方向的夹角记为γ,矢量v1矢量n之间的夹角记为β。

图1 并联机构模型Fig.1 Parallel Mechanism Model
故有||vi||=1。针对描述输入端运动副转动轴的方向矢量ui的几何关系有:

式中:ηi—三条运动支链分配角度关系的参数;取 ηi=2(i-1)π/3,标志着三条运动支链以120°均匀分配在静平台的一周,由此:

由于 ηi=2(i-1)π/3,γ、α1、α2为常量,在方程组中就存在 θi、vx、vy、vz四个未知数,只凭借两个方程无法求解,故引入正切与余切半角公式,取第一运动学支链为计算目标,有η1=0、γ=π/3、α2=π/2,将代入式(3)中进行计算可得:

2.2 3-RRR球面并联机构运动学雅可比矩阵
一般来说,运动学的速度方程可以利用运动学的位置方程通过对时间的一阶偏导数方程进行描述,首先利用上述并联机构所建立的数学模型:

各个终端绕该轴的角转速可用一向量σ进行表示,如图2所示。其中,绕着轴σ,速度vi(t)经过Δt时间后的速度变为vi(t+Δt),根据向量的叉积可表示为:v˙i=σ×vi,按照这种原则,将矢量wi、ui写成关于并联机构三条运动链电机输入角加速度的表达形式为w˙i=θ˙i·ui×wi。
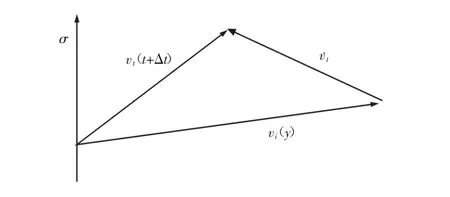
图2 角速度向量与线速度向量的叉乘关系Fig.2 The Relationship Between the Angular Velocity Vector and the Line Velocity Vector
即:若已知并联机构输入θ˙i可以对机构末端输出v_i进行求解,即运动学正解问题;若已知其末端输出vi的角速度γ可以求解并联机构的输入θ˙i,即运动学反解问题,可进一步验证关于并联机构运动学正反解一体的特性,进而得出关于该机构的运动学反解的雅可比矩阵为:
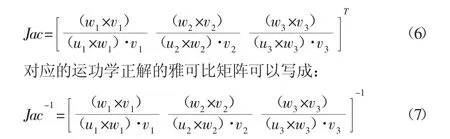
3 基于遗传算法结构优化
3.1 优化目标的选择
为了后续方便计算,将式(7)记为 Jac=[J1,J2,J3]。

式中:ηi已知,α1、γ、θ、vx、vy、vZ作为结构优化对象,针对结构进行优化的基本原则为工作空间最大化,在此引入雅克比矩阵的条件数,描述方程为式中:J-1—雅可比矩阵的逆;|·|||—矩阵的任意范数;一般取欧几里得范数(Euclid范数)。
雅可比矩阵的条件数是一个大于等于1的正数,其存在的意义在于,当kj越接近于1,说明机构的灵活性越好,反之灵活性变差,故此处取kj作为优化目标。鉴于优化目标中存在较多的待优化参数,为解决传统算法搜索全局性差,存在漏解,且雅可比矩阵计算量较大,整个流程花费时间较长等问题,在此提出一种遗传算法针对雅可比矩阵的条件数方程进行优化。
3.2 基于遗传算法结构优化
遗传算法是一种模仿达尔文生物进化机制,实现计算机并行搜索的数值优化方法,遗传算法的主要计算流程可以概括为:
(1)编码:计算之前要将实际数据预处理成为待计算编码,目前应用较多的有一般二进制编码和实数编码;
(2)种群初始化:生成基因编码的定义区间,从该区间内随机产生父代基因,种群POP的规模越大算法搜索的全局性越好,但对应的计算复杂度也越高;
(3)适应度计算:在求解全局最大值的优化问题当中,适应度函数FitFun(x)通常选择目标函数F(x)本身,将各编码值带入计算适应度值。
(4)选择:一般采用转轮式选择法,按照所占转轮比例随机地进行个体基因编码的选择和淘汰,被选中的基因进行下一代计算,淘汰的基因则从待解集中删除;
(5)交叉和变异:以一定概率(交叉概率)挑选一对基因,从指定的编码位置断开分别交换另一半编码链组成新的基因。以一固定的概率(变异概率)在新的基因链中选取某一个编码进行变异,实数编码变异范围是(0~9),二进制变异则0、1相互转换,进而生成新一代的基因编码;
(6)重复以上步骤(3)~(6),直到目标收敛获得最优解或达到其他停机条件。
针对上述并联机构遗传优化问题的重难点主要集中在适应度函数的构建上,因为其中的待优化参数vx、vy、vZ无法直接写出表达式,且以一定形式与 α1、γ、θi、α2相关联。若直接利用计算机搜索的方式将vx、vy、vZ进行赋值计算难免会强行割裂其与待优化参数 α1、γ、θi、α2的关系,故此处在上文的基础上,利用 tanθi/2 替换掉sinθi与cosθi,将问题转化为多项式的根值存在问题,将根值存在的判断式引入,作为适应度函数的判别方程:

由于雅克比矩阵的条件数kj为一个≥1的正数,故建立用于遗传算法优化的适应度函数为:

此时适应度函数的返回值为1-kj≤0,在进行适应度选择时kj的值越接近1,函数的返回值越小,这样可以按照适应度值的大小进行排序和筛选。
改进适应度函数后遗传算法流程,如图3所示。

图3 遗传算法的流程图Fig.3 Flow Chart of Genetic Algorithm
对于判断优化结果是否达到最优解,引入以下判别方程:

其中,i、n数值根据计算的进程而变动,旨在将一段连续时间内适应度函数差值的总和进行监督,监督值ε按照适应度函数的变化情况取0.00001。同时将单运动学支链的末端输出矢量也纳入待优化的范畴,引入约束:v2x+v2y+v2z=1。
根据该机构的结构特性和遗传算法的运算合理性,设定遗传算法优化并联机构相关参数,如表1所示。

表1 遗传算法中的各参数Tab.1 Parameters in the Genetic Algorithm
按参数对雅可比矩阵条件数进行优化,得到遗传算法的适应度变化,如图4所示。图4中虚线代表在优化计算过程中各种群适应度的平均数变化曲线,出现波动的原因在于,在子群适应度不满足适应度判别方程Fs时,函数返回值被强行置为-1以便于淘汰该数据,实线则代表每代子群中最佳适应度的变化曲线,最终在123代达到全局最优解。对比文献[7-8,10]中的各组优化结果,如表2所示,本方法1/kj=0.999992,可见机构的运动灵活性得到了显著提高。此时雅可比矩阵的条件数kj=1.000008,其余各优化目标,如表3所示。

图4 遗传算法适应度变化情况Fig.4 Genetic Algorithm Adaptability Changes

表2 各方法优化结果对比Tab.2 Comparison of Methods to Optimize the Results

表3 各优化参数Tab.3 Optimization Parameters
根据以上优化结果搭建的物理样机模型,如图5所示。通过步进电机驱动,采集其末端动平台的运动轨迹离散点,如图6所示,可见其工作空间近乎一个完整的球面,仅在球面两端出现很小工作空间空白,达到了优化设计目标。

图5 物理样机Fig.5 Physical Prototypes Based on Optimization Results

图6 模拟工作空间分布情况Fig.6 Optimized Simulation of the Work Space Distribution
4 结论
为提高3-RRR球面并联机构的运动灵巧性、扩大有效工作空间,提出了一种智能遗传算法对机构中各关键参数进行优化,为保证机构的结构特性,引入了适应度函数的判别方程和约束方程,有效的将并联机构的雅可比矩阵条件数控制在1.000008。相比国外学者对应的指标参数具有一定的优势。据此搭建物理样机进行实验验证,结果表明优化后的3-RRR并联机构显示出更强的工程实用性,具有更广阔的应用前景。
