惯性圆锥破碎机主轴的动力学特性分析

周弘扬，王春雨，巩云鹏

（东北大学 机械工程与自动化学院，辽宁 沈阳 110819）

1 引言

惯性圆锥破碎机是一种具有物料选择性的细碎破碎机。它与标准圆锥破碎机相比耗能更低，效率更高，因此被广泛应用于冶金、矿山、建材等行业。

然而，在惯性圆锥破碎机的故障中，主轴断裂是非常严重的。一旦发生断裂，其维修成本很高，从而对企业造成较大的经济损失。为了确保惯性圆锥破碎机安全、可靠运行，对主轴进行静强度分析十分重要[1]。

在国内圆锥破碎机主轴的力学研究中，文献[2]对弹簧式圆锥破碎机主轴进行了受力分析。通过主轴上的偏心轴套给主轴下端的反力对悬挂中心的力矩与破碎力、球面瓦给动锥的支持力对悬挂中心的合力矩的平衡计算出主轴所受到的力。文献[3]对弹簧式圆锥破碎机主轴的受力采用几何计算方法利用主轴上的偏心轴套给主轴下端的反力与破碎力、球面瓦对动锥的支持力三力平衡对主轴受力进行了分析。文献[4]利用ANSYS分析软件，将惯性圆锥破碎机的动锥、动锥衬板和主轴作为一体建模，将单位破碎力施加在动锥衬板上间接对主轴的进行力学分析。这些文献中少有对惯性圆锥破碎机主轴进行直接的受力分析。

通过计算激振力得到惯性圆锥破碎机的最大破碎力，进而计算出最大破碎力引起的激振器对主轴最大作用力，对惯性圆锥破碎机主轴受力进行了直接的分析。最后，使用ANSYS APDL分析软件对惯性圆锥破碎机主轴进行静力学分析与模态分析，以期为其主轴的设计提供一定依据。

2 惯性圆锥破碎机的原理及特点

惯性圆锥破碎机机体安装在隔振装置上，破碎元件主要由定锥和动锥组成，动锥与定锥上安装有耐磨衬板，动锥衬板与定锥衬板之间形成破碎腔。主轴上端与动锥相连，主轴下端通过轴套与偏心激振器相接。电动机旋转通过传动机构带动固定在轴套上的偏心激振器，偏心激振器旋转产生激振力，激振力通过主轴传递给动锥，使动锥绕球面瓦作球心运动。当破碎腔内有物料时，动锥伴有强烈的高频振动，对物料进行冲击、挤压以此来破碎物料。当破碎腔内落入不可破碎物体时，由于动锥主轴与偏心激振器之间无刚性连接，虽然动锥被不可破碎的物料卡住而停止运动，但偏心激振器会继续转动，不会发生传动系统的破坏。

具有料层选择性是惯性圆锥破碎机相比于普通圆锥破碎机的重要特点。由于惯性圆锥破碎机沿物料晶格方向破碎，所以破碎力大，破碎效率更高，而且可以破碎硬度更大的物料。惯性圆锥破碎机安装在二次隔振装置上，不与大地相连，工作噪音小，操作安装拆卸更方便。

3 主轴的受力分析

3.1 最大破碎力的计算

惯性圆锥破碎机的破碎力本质上是由主轴上的偏心激振器的离心力与动锥高速旋转产生的惯性力提供的。由于动锥沿物料表面碾过时章动角速度很不稳定，因此无法准确计算出惯性力大小。假设物料是均匀地分布在整个破碎室的，破碎机惯性力就可以在近似无载的情况下计算出来[3]。此时破碎机的破碎力最大，如图1所示。

图1 最大破碎力的计算Fig.1 Calculation of the Maximum Crushing Force

式中：F0—偏心激振器惯性力；m0—偏心块质量；m1—动锥质量；ω—进动角速度；l1—动锥质心A点与o点连线的长度；l0—偏心块质心B点与o点连线的长度；β—动锥中心线与定锥中心线的夹角；δ—偏心块质心和o点连线与动锥中心线的夹角；lF—最大破碎力作用点到o点距离。

通过对o点取矩，可得最大破碎力Fmax为：

3.2 主轴受力计算

激振器对主轴作用力可用破碎力计算，如图2所示。正常破碎力与动锥重力合成F′力，其值为：

F′作用线与偏心激振器产生的惯性力的作用线交于c点，根据在同一平面内互不平行的三个力相互平衡，力作用线必汇交于一点定理，球面轴承对动锥的支持力必通过c点且该支持力的作用线通过动锥球面座中心o，根据图2的几何关系，可求出Fp为：

式中：Fp—正常破碎力引起的激振器对主轴作用力；Fq—球面轴承对动锥的支持力；θ1—力 F′与 Fp之间的夹角；θ2—力 F′与Fq之间的夹角；δ1—力F′与F之间的夹角；β—动锥中心线与定锥中心线夹角；γ1—动锥锥面倾角。

图2 惯性圆锥破碎机主轴受力分析Fig.2 Stress Analysis of Inertia Cone Crusher Spindle

根据图2几何关系，可得：

由式（8）推导出式（9）为：

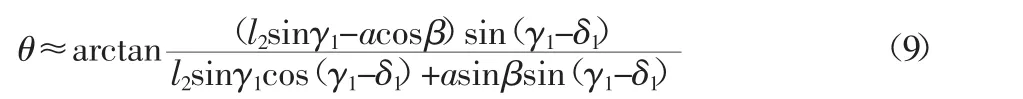
将式（4）、式（9）结果代入式（3）可求得 Fp。最大破碎力引起的激振器对主轴最大作用力Fpmax与上面求法相同可求得Fpmax=3.87×106N。

4 有限元静强度分析

4.1 主轴有限元模型的建立

主轴材料为超高强度合金钢42CrMo，该材料密度7.85×103kg/m3，泊松比为0.28，弹性模量为212GPa。主轴长1050mm，最小轴径93mm，与动锥过盈配合的轴段为直径140mm与直径200mm轴段，各截面变化处都进行了倒角及圆角处理。该主轴结构尺寸，如图3所示。

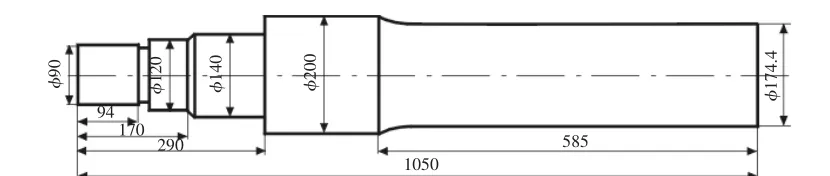
图3 主轴结构尺寸Fig.3 Size of the Spindle

主轴划分网格时采用由面单元通过拉伸网格产生体单元的方法建立有限元模型。首先建立关键点并形成轴截面，使用布尔运算利用工作坐标系将轴截面分割成若干个规则的四边形。采用PLANE182单元利用映射网格划分方法进行面单元网格划分，然后通过拉伸网格生成由20节点SOLID186体单元组成的有限元模型[5]。整个模型包含122166个节点，60640个单元。

4.2 主轴约束和载荷的施加

根据惯性圆锥破碎机的实际工作情况，对主轴的上下端面进行全位移约束。主轴中部φ200圆柱面与动锥内圆锥面为过盈配合，故对此圆锥面进行全位移约束。

当偏心激振器旋转产生离心力时，该离心力会作用在偏心激振器内圆柱面与主轴外圆柱面的切线上，由图2可知，最大破碎力对主轴的作用力Fpmax与偏心激振器与主轴的激振力平衡，故在该切线上施加Y方向，大小为Fpmax的力[6-10]。

4.3 主轴的静力分析结果

主轴在静力作用下的等效应力云图和位移云图，如图4、图5所示。

由图4可知主轴最大变形量为0.64mm，发生在偏心激振器内圆柱面与主轴外圆柱面的切线上。最小位移量为0，发生在主轴两个端面与中部固定处。主轴变形的趋势是向轴线凹陷。

由图5可看出最大应力发生在激振器与底部圆柱面接触处，最大应力为770MPa，小于材料屈服强度。另外，底部圆柱面与中部固定圆柱面结合处应力集中较大，而在实际工作中，主轴承受很大的振动冲击载荷，此处容易发生断轴事故，故需要适当增大过渡圆角，减小应力集中。

图4 主轴位移云图Fig.4 Displacement Vector Sum of the Spindle

图5 主轴等效应力云图Fig.5 Von Mises Stress of the Spindle

5 主轴的模态分析

在已经建立的主轴有限元模型上重新加载约束。根据主轴实际工作情况，在主轴的两端面施加全位移约束，在动锥与主轴接触的圆柱面施加全位移约束，采用ANSYSAPDL中的BlockLanczos法进行模态分析，并设置提取，分析主轴的前6阶模态振型及固有频率，如图6所示。各阶固有频率计算结果，如表1所示。

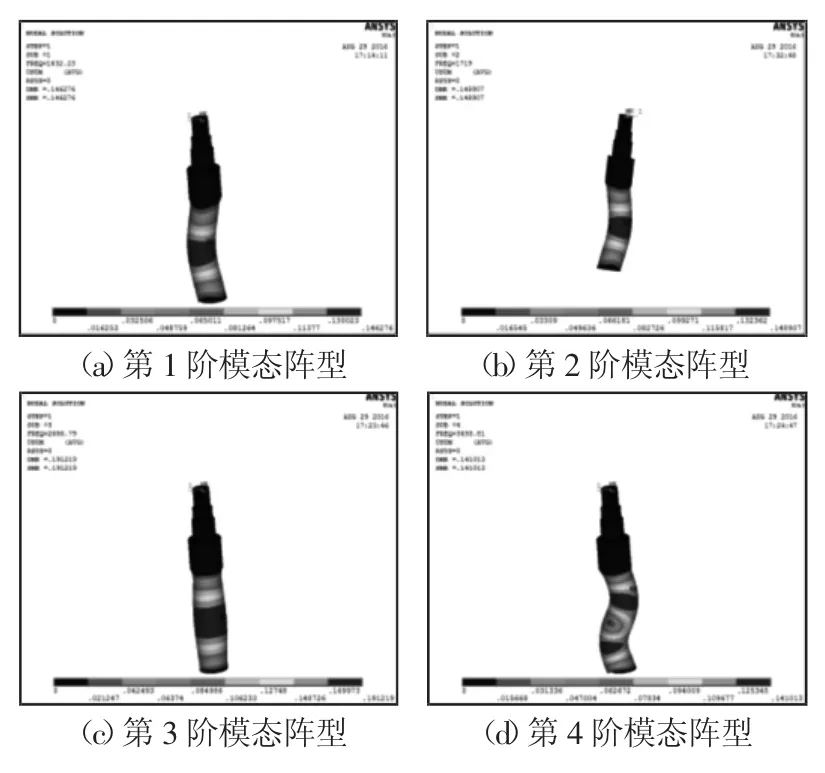
图6 主轴前六阶模态阵型图Fig.6 The First Six Order Modal Shape of the Spindle

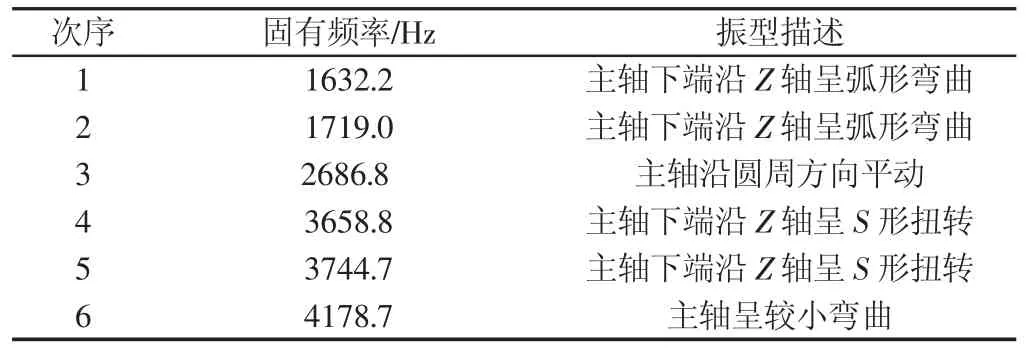
表1 前六阶模态的固有频率Tab.1 The Six Eight Order Natural Frequency of the Modality

由图6可知，主轴主要变形部分为主轴下端与激振器接触的内表面，主要沿z轴方向呈波浪型弯曲振动。第三阶振动最剧烈，出现程度较轻的膨胀爆炸状。第四阶，第五阶主轴发生扭转变形，且变形十分明显，设计时需要加强主轴的刚度，强度。

6 结论

对惯性圆锥破碎机主轴进行了受力分析，为主轴的受力计算提供理论依据。利用有限元软件ANSYS APDL对主轴进行了静强度分析与模态分析，获得了最大破碎力下主轴的应力和变形分布规律和主轴各阶的固有频率及相应模态振型。通过计算主轴最大等效应力来校核主轴工作的安全性，通过位移云图和等效应力云图及固有频率及固有振型为惯性圆锥破碎机主轴的力学分析和动力学分析提供理论依据。（1）主轴最大变形发生在偏心激振器内圆柱面与主轴外圆柱面的切线附近，最大变形量0.64mm，符合刚度要求。主最大应力发生在激振器与底部圆柱面接触处，最大应力为770MPa，小于屈服强度930MPa，强度满足要求。（2）惯性圆锥破碎机激振器旋转频率约为81Hz，远小于主轴各阶固有频率，因此破碎机工作时不会发生公共振现象，能够正常工作。（3）主轴是破碎机中主要的工作零件，承受破碎力很大，非常容易失效，仅对惯性圆锥破碎机主轴进行静强度分析不够全面，但可为后续疲劳强度分析等力学分析提供一定依据。