面向混合约束模型的线缆布线技术研究

李春泉，王弘扬，尚玉玲，周远畅

（桂林电子科技大学 机电工程学院，广西 桂林 541004）

1 引言

线缆作为汽车电子技术和产品的物理载体，有着至关重要的地位。随着机电装备日益复杂的趋势，线缆数量和类型的增加，导致机电装备内部空间紧张。现有的布线方法已经不能完全适应于当前环境[1]。线缆布局是一项复杂的工作，广泛运用于许多工程领域，如机械、化工、建筑等。因为在大多数情况下，线缆布线设计是连接到工程设计的重要组成部分。在实际布线过程中，基于不同的布线约束[2]，可以以不同的方式获得最佳的线缆路径。因此，在线缆布局设计中，如何使布线结果是最好的（或更好）一直是一个主要的研究方向。

近年来，众多专家学者针对布局问题进行了研究，并取得了较多的研究成果。文献[3-4]针对空间布局问题，对基本情况进行了分析与综述，同时提出了较好的解决方法。文献[5]针对线缆自动布局设计问题，提出一种基于障碍物与目标吸引的改进快速随机树算法，能高效地完成线缆自动布线。文献[6-7]采用三维加权网格对发动机复杂三维模型进行网格划分，利用改进的Lee算法以及最小斯坦树生成法，开发出航空发动机网格敷管系统。文献[8]提出一种以线缆几何模型信息与线束模型信息为核心，采用B样条曲线拟合的装配模型，对线缆布线设计过程进行仿真。由于目前线缆布线影响布局设计的约束因素过于繁杂，使得无法找到一个适用于各种约束环境的适用性方法。

因此，在相关研究工作的基础上，建立一种布线混合约束模型，把布线问题描述为满足一定约束的路径搜索问题。首先，提出了约束因子、约束集合等相关概念，将布线过程中所需要的约束定义为不同的约束因子，并对不同的约束因子进行划分，使约束功能类似约束因子组合成为相关的约束集合，每一个约束集合对应一个布线规则，使布线约束系统化。其次，将相应的布线规则进行整合，并建立布线混合约束模型。最后，对该模型进行了实例验证。

2 线缆布局设计的约束因素分析

为了便于分析与理解布线过程中各约束，我们定义了以下基本概念。

2.1 概念的定义

定义1：约束因子CF（constraint factor）在布线过程中，对布线方案设计具有影响的因素，并在设计过程中具有一定独立性的基本约束单元的设计变量。如线缆预留长度、最小弯角半径、绑扎点位置、折弯半径等。

定义2：约束集合CS（constraint set）将约束功能类似的约束因子组合形成相关的集合 CS=｛CF1，CF2，CF3，…，CFn｝。约束集合具有可扩展性和继承性。

约束集合有子集（Sub CF）与父集（Super CF）之分，子集与父集的关系是相对的，约束集合的关系结构图中SubCF1既是SuperCF的子集，又是SubCF11的父集，一个父集有多个子集，子集对父集具有继承性，如图1所示。

图1 关系结构图Fig.1 Relationship Structure Diagram

对于不同的布线布局问题，影响布局设计的约束因子是不一样的，这使得约束的类型和数量是不确定的。通过对约束因子和约束集合的定义，对约束因子进行了分类，将具有相似约束功能的约束因子进行分类组合并建立相应的约束集合。

2.2 约束因子的基本分类

线缆布局设计应用在不同情况时虽具有一定的差异，但其约束因子的本质却相差不大。

根据约束因子的分类原则和各约束因素的功能和属性，将约束因子分类归并到以下不同的基本约束集合中，如图2所示。

图2 约束因子分类Fig.2 Constraint Factor Classification

2.2.1 设计规则约束集合

DCS是由与线缆机械性能有密切关系的约束因子组成的集合。一般是指在线缆布线经验上而提出的约束。如，较长的线缆应沿车身体、结构体等支撑物布线，便于固定线缆。这是结构约束，它与线缆的机械性能有着密切关系。线缆应该尽可能多的通过已经布好的线缆的路径，使线缆变成线束，这样有助于节约布线空间和便于操作管理。如有频繁操作的开关等应尽量安装在方便的地方，或者线缆布线路径对于维修必须是一条避开所有元件的可行路径，这是可行约束，他与线缆维修、运行的方便程度有着密切的关系，等等。

2.2.2 位置约束集合

PCS是由与线束在实际布线过程中的位置确定有密切关系的约束因子组成的集合。一般是指结合线束在实际布线过程中的位置，线束的实际走向是根据布线过程中所涉及的诸多因素进行综合考虑之后进行排布的。考虑到线束的低垂、移位、质量、固定方式和固定位置的方便性而提出的约束，在布线过程中必须考虑有足够、合理的固定点和固定方式，这样才能保证布线过程具有一定的可靠性。

2.2.3 工艺约束集合

TCS是由与线束布线工艺有密切关系的约束因子组成的集合。一般是指在实际布线过程中根据线缆的形状、尺寸、相对位置和性质并结合线缆生产过程中的工艺过程而提出的约束。工艺约束还包括：折弯半径、折弯最大根数、绑扎间距、绑扎点个数、预留长度等[9]。

2.2.4 形状约束集合

FCS是由与线缆几何形状有密切关系的约束因子组成的集合。一般是指满足线缆受力要求和自身材料限制的约束。其表现在很多方面，如：线缆布线时应尽量减少弯曲，避免线缆受到较大的应力。如必须弯曲时，线缆的弯角尽量≥90°，与此同时还必须满足线缆的最小弯曲半径。为了防止连接器发生位移从而降低了线缆的可靠性，线缆连接器接头应采用刚性固定。在考虑到线缆的热伸长的影响，截面积较大的线缆线芯应采用绞合分裂的线缆。线缆布线应该保证其稳定性和牢固性，避免由振动和冲击所引发的失效和安全隐患。线缆的放置应该按照特定要求，不应出现卷曲、大量弯折等情况[10]。

2.2.5 结构约束

SCS是由与线缆结构信息有密切关系的约束因子组成的集合。一般是指满足线缆线缆基本属性和组成元素之间的约束。其表现在很多方面，如：根据线缆的结构信息，我们可以知道线缆任何控制点之间的连接关系，在此基础上，将基本属性信息和附加信息进行关联，即可构成线缆几何模型信息的数据来源。

通过对约束因子的基本分类之后，可以使用约束集合来定义和管理约束因子。应该指出的是，约束因子的基本分类并不意味着约束集合也随之确定，约束集合是具有继承性和可扩展性的，将基本的约束集合进行变换，也可派生出新的约束子集，通过变换和派生可以解决不同的布局问题。

3 基于布线混合约束模型的线缆布线算法设计

利用线缆的布线混合约束模型进行布线设计，可以使布线设计过程中所需要考虑的约束系统化，将不同约束分类应用于不同的设计场合，更能提高布线设计效率。在实际布线过程中，通常需要满足多种复杂条件，在本实例中只针对布线混合约束模型中重点考虑的布线规则进行分析和验证。为获得较优的线缆敷设轨迹，将线缆的总长度作为目标函数，将布线设计中必须满足的要求作为约束条件。其数学模型描述如下：

表示线缆与障碍物不能发生干涉，式中：｛w1，…，wk｝和｛b1，…，bk｝分别为线缆和障碍物的集合。

表示弯角半径应大于线束半径的6倍，且不得小于最大线缆半径的10倍，式中：Bend—线束弯角半径；D—线束半径；d—最大线缆半径。

表示为保证线缆的有效性，在接插件端子处给予一定的松弛量。其值不应该小于

式中：d_fixture—线缆与其它静止机件间的最小间隙距离，为避免

线缆发生磨损及影响其性能，其值不应小于L2。

表示为保证线束容量不出现过盈现象，式中：线束容纳的线缆数量不应小于规定的线束容量R，I—线束容纳的线缆数量。

表示管路中两段线缆的夹角，其值不小于π/2。

表示线缆起点和终点延长出的直线段，长度不小于L4。

3.1 模拟退火算法的基本思想

模拟退火算法：通过初始解i和控制参数初值t对当前解重复进行“产生新解→计算目标函数差→接受或舍弃”的迭代，并进行渐进衰减t值，根据蒙特卡罗迭代求解法的启发式搜索过程，当算法终止时的当前解即为所得近似最优解。在算法进行时退火过程由冷却进度表（Cooling Schedule）控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。

3.2 模拟退火算法的实现过程

Step 1：参数初始化，产生初始解 x0∈Ω，其中，Ω＝｛（x1，x2，…，xm）|xi∈｛0，1｝｝为所有可能解的集合，xi表示第 i个最优路径点，计算相应的目标函数值W0，给出控制参数初值T0，Mapkob链长度N以及停止参数Tλ，设定最大迭代次数β；

Step 2：确定初始解是否可行性，若不可行，则进行调整，否则转3；

Step 3：产生新解，判断新解的可行性，计算新解与当前解的目标函数值差 ΔW，根据式（10）计算接受概率 P（ΔW，T），取在（0，1）上均匀分布的随机数 θ，若 P（ΔW，T）＞θ，则接受新解，否则放弃新解。

Step 4：计算迭代次数n，若n＜N，则在此温度下的迭代尚未结束，未完成一个Mapkob链长的迭代，转步骤3；

Step 5：判断是否满足算法的终止准则，若迭代次数小于n最大迭代次数β且T＞Tλ继续降温，令T=T×α，其中α是降温因子，继续转步骤3，否则，算法终止，输出当前解。

4 应用实例

针对研究的复杂约束环境下的布线技术的内容，对某机箱部件进行线缆布线。在该实例中，采用约束条件为：L1≥2mm，L2≥10mm，L3≥50mm，L4≥70mm，angle≥π/2，D=15mm，Bend＞90mm；d=6mm，Bend＞60mm。采用MATLAB软件进行编程和仿真，线缆端点坐标分别为 A（2，12），B（12，2）。在满足约束模型的情况下，分别采用模拟退火（Simulated Annealing）算法、蝙蝠算法（Bat Algorithm）、粒子群（ParticleSwarmOptomization）算法进行计算仿真，完成了布线，并将仿真结果进行对比，验证了该约束模型计算的可行性。运行50次且最大迭代次数为200，将模拟退火算法（SA）、蝙蝠算法（BA）、粒子群算法（PSO）运算结果进行对比，如表1所示。

表1 参数意义说明Tab.1 Parameter Meaning Description

图3 收敛曲线Fig．3 Convergence Curve

图4 线缆布线图Fig．4 Cable Wiring Diagram

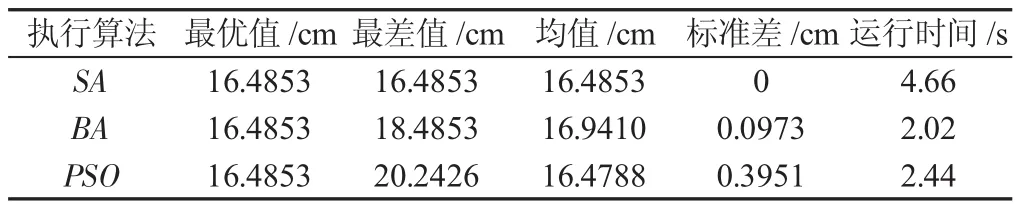
表2 算法对比Tab.2 Algorithm Comparison

由表1可知，模拟退火算法（SA）运算结果稳定，标准差为0，寻优率最高。

5 结论

针对线缆布线方法问题，提出了一种基于布线混合约束模型的布线方法。结论如下：（1）该方法有效的满足了一系列约束，并能够实现基于布线混合约束模型的走线方式。（2）根据约束因子、约束集合等概念有效的解决了在错综复杂的布线环境中，运用布线混合约束模型，生成了路径，取得了较好的布线成果。（3）通过实验，将模拟退火算法（SA）、蝙蝠算法（BA）、粒子群算法（PSO）运算结果进行对比，验证了该方法的有效性。