综合楼宇火灾疏散路线研究

张豪 何梦瑶 王渊博

综合楼宇内人员密集，且人员成分复杂，有很多楼层为了添加功能分区，随意添加隔断，造成过道窄小。在一座功能全面的大厦内拥有门厅、走道、办公用房、公共用房、设备用房、服务用房等。在面临火灾事件时，指挥疏散难度较大。由于疏散起点和终点数量多，疏散路线繁杂，人员往往缺乏相关培训，应急反应能力不足，使之无法在短时间内做出正确反应，使二次意外发生率高。本文着重分析了综合楼宇火灾突发疏散路线最优构建，以北京石油化工学院康庄校区综合楼为例，利用定量的计算方法，为综合楼宇应急疏散路线做出提前规划，提高楼内人员的自救疏散能力。

本文主要研究以救援总时长最短为目标的应急疏散方法，构建模型，提出可广泛在综合楼宇中使用的应急疏散方法，建立应急疏散空间网络模型和性能变量，分析应急疏散的空间，计算应急疏散路线的最优化及动态模拟分析，并针对具体场景进行了应用验证。

应急疏散空间网络模型和性能变量

疏散空间是由不同的节点和通道网络组成，各节点和通道都有多个属性是动态的，比如剩余疏散距离、疏散时间等等，这些都是疏散过程中的成本，在灾难与疏散同时进行的过程中，各个疏散通道以及出口的成本会发生着变化，是一个随时间变化的函数。

空间模型。把任一疏散空间K 网络化并且利用三维空间坐标来表示各个节点在整体中的位置关系。例如V1（X，Y，Z），节点集为 V＝｛V1，V2，…，Vn｝。节点分为起始点，疏散过程点，以及疏散出口点。任意节点可以定义为

Vi（x，y，z），Pi（t），Dim（t），Ai（t），Ci（t），Zi（t）

其中，X，Y，Z代表节点在空间中的坐标，Pi（t）表示t时刻节点i 处剩余疏散路径长度；Dim（t）代表t 时刻i节点的事故状态，Dim（t）＝0表示无事故发生；事故发生的概率为Qm，其中m∈α，α表示所有可能发生的事故以及状态。

Ai（t）代表t时刻节点i 处的疏散队伍长度，Ci（t）表示t时刻内从节点i在通道Kij疏散完毕人数。

Zi（t）表示t时刻节点i的滞留人数，Zi（t）＝Ai（t）- Ci（t）。

性能指标。设Bb（t）为t时刻任一疏散人员的生存状态。Bb（t）＝1 则表示存活，Bb（t）＝0则表示

死亡。B（t）表示t时刻内整个疏散空间内存活人数，能直接体现疏散系统的性能。设M（t）为t时刻疏散成功人数。

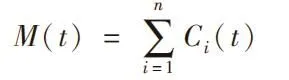
疏散成功人数以及在疏散空间内安全存活人数都是评价疏散系统性能的重要指标。

疏散空间剩余步行距离。t时刻处于疏散空间内所有人员距离出口剩余步行距离可定义为：t时刻内疏散空间内剩余人数，距离出口的步数。

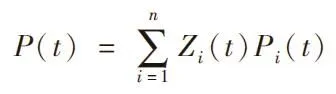
剩余步数直接反映了应急系统的疏散能力，通道的复杂程度，最大同时通过人数以及排队的情况。如果定义P（t）＝0是假定所有人员疏散过程中互不干扰，以最快速朝最近的出口移动。初始状态所有通道Pm（0）＝0，那么随着时间的变化计算出Pm（t）。如果结果趋近与Pt（0），则可以认为该疏散通道疏散能力强。

疏散通道安全等级。在任一节点至另一节点路程中为一个节点集。设V3V'4为节点V3经过一系列节点至V4的路程。如果V3V'4路程中所有节点都符合D（t）≤s，那么可以定义V3V'4通道是安全的。安全等级为s。

应急疏散路线的最优化及动态模拟分析

在任意时刻，任意初始点，疏散人员在危险等级最小路线能以最快时间疏散完毕，则为最优路线。假设整数N为出口，假设下式成立，｛tj｝表示节点j 到出口N 最优路线的时间。｛tij｝则表示节点i 到节点j 通道的整体时间属性，Ti表示通道可安全疏散的时间属性。

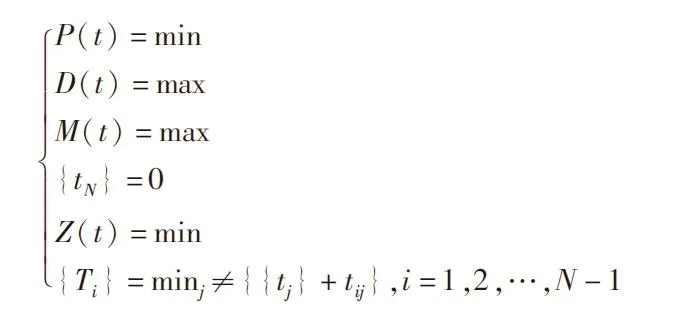
将上述方程组初始化

当疏散进行到L＝1，2，3，…，时间段，可得到

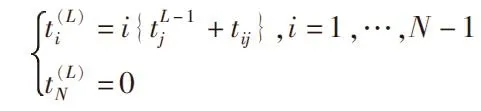
如果随着时间，某通道内或某节点的事故无法被利用，那么时间属性则为无限大，代表无法从该通道通过。可以重新定义时间属性，令其他通道时间属性不变，重新进行优化计算，得到最优路线。

实例研究——北京石油化工学院综合楼二楼

基本情况。图1所示为北京石油化工学院康庄校区综合楼二楼平面图，综合楼一共5 层，各层分布一样。在此以二楼举例。疏散出口可以以（1）出口为主要疏散出口，（2）和（3）为辅助疏散出口，窗户也可以当做疏散出口目标节点。当然事故发生的时候，如果楼梯可以利用，疏散个体通常会选择熟悉的楼梯来进行疏散。所以疏散个体从各自起始节点（教室门牌号）出发，疏散经过走廊，然后通过楼梯向疏散出口（1）、（2）和（3）疏散。小概率选择从窗口向地面的逃生方式，这种方式疏散距离短，但是疏散成本较高。但随着灾难发生时间的推移，灾难变得严重，疏散个体的心理状态会影响个人判断与选择。当疏散出口（1）、（2）和（3）不能疏散，那么窗户向地面的逃生方式的成本相对而言变低。

根据网络空间图进行路线规划。定义疏散成本为整数，即不考虑灾难演变对于疏散通道和节点的影响。如图2所示，疏散人员在各节点各通道以一个平均速度进行疏散时，相同通道在进行相反方向的疏散时，所需时间不一定相同，路程最短的路线不一定是点到点的最佳路线。所以运用动态分析法可以得出各个起始点至最终目的点的最佳路线，用集合表示为

图1 综合楼二楼平面图

｛（203，32）（202，32）（201，32）（32，40）（40，3）｝

｛（204，33）（33，41）（41，2）｝

｛（213，34），（215，35）（205，36）（207，37）（34，1）（35，1）（36，1）（37，1）｝

｛（206，38）（209，38）（211，39）（38，42）（39，42）（42，1）｝

例如（32，40）表示从节点32向节点40移动，表达疏散个体移动的路线以及方向，定义疏散成本是随时间变动的额函数，即随时间的变化各个节点或通道的疏散成本发生变化。当通道无法通过时，疏散成本最高，这时就要考虑其他可行通道，并结合疏散个体自身属性，重新进行选择。

当某时刻t 时，201 向通道32 的出口节点损坏，无法通过。通道（201，32）无法使用。那么动态分析，处于节点201 的疏散个体最优的疏散路线为｛（201，10）（10，21）｝。

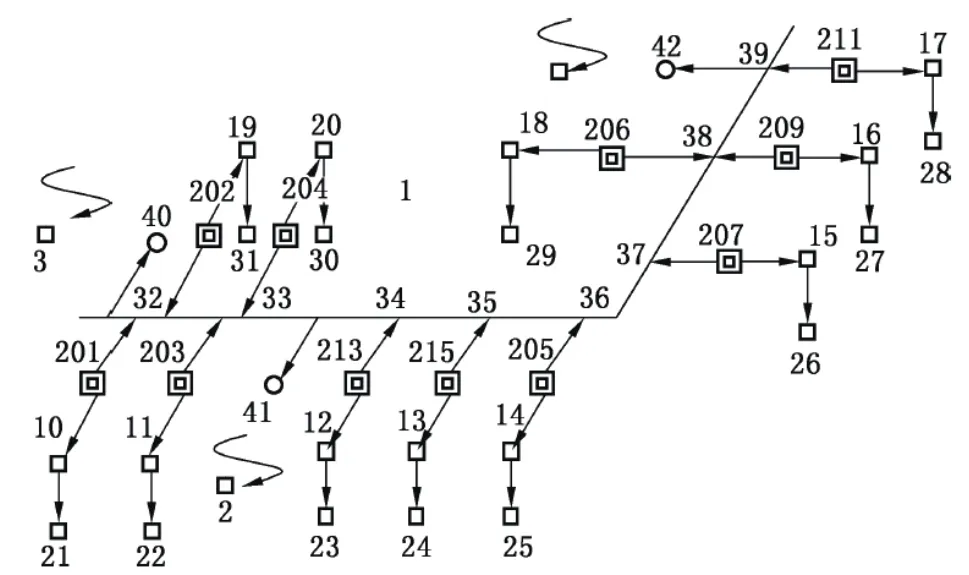
图2 疏散路线网络空间图

如果通道属性发生变化，上层楼层各节点与通道对于路线也应做出相应调整。

研究结论

应急疏散路线研究是一个应用性很强的课题，对保护人的生命安全具有重大的意义。在火灾事故中，实时的危险都是动态的。本文利用最优化理论，通过上述分析明确疏散路线，对疏散进行最优化评价，根据建筑空间网络中各节点和通道的动态属性，实时调整最优疏散路线。并结合用户反馈和反复实验产生的误差，使疏散路线根据实时动态危险做出相应的路线调整和自救方式的提醒。为今后在实际生活中的应用，提供了理论基础。