动目标异源雷达相参配准研究*

， ，

(1.装备学院研究生管理大队， 北京 101416；2.装备学院光电装备系， 北京 101416)

0 引言

近年来，人们开始关注利用几部处于不同频段独立工作的雷达，通过异源雷达带宽相参合成技术，在信号层实现一个等效的大带宽，达到大幅提高距离分辨率，且保持原有独立工作雷达威力的目的[1-4]。解决了单雷达系统单纯通过增加带宽来提高距离分辨率带来的成本、制造工艺以及威力等方面的巨大难题[1,5]。为目标识别、导弹防御等军事领域提供了目标更加精细的一维结构，具有重要的学术价值和现实意义。

文献[6]最早论述了静止目标异源雷达间的非相参因子为线性相位差异和固定相位差异，以及其来源和估计补偿方法，但是没有对动目标展开研究；文献[7]首次研究动目标异源雷达相参合成问题，将非相参因子分解为二次、线性、固定相位差异。并以某部雷达为参考，其他雷达数据乘以非相参量，构造表征各雷达间相干性的相干函数，利用遗传算法进行全局优化，求出3个非相参量并补偿。然而这种方法相干函数的待求量太多，全局优化计算量很大。文献[8]对两雷达观测同一静止目标成一维距离像，并以某部雷达为参考，平移另一个一维距离像，累加各距离像并求图像熵，依据最小熵准则求线性相位差异。这是一种优秀的算法，但是搜索熵的最小值遍历了所有的采样点，计算量很大。文献[9]对静止目标基于数据相关求解线性相位差异并补偿后，建立只含固定相位差异的相干函数，以某一步长全局搜索固定相位差异。文献[10]对文献[9]作了改进，提出无需各雷达建模外推数据的相参配准方法，降低了算法复杂度的同时避免了外推误差。

本文主要研究动目标异源雷达相参合成问题。在分析动目标幅相差异模型的基础上，直接利用各子带估计目标速度，在子带作速度补偿，剩余的相位差异模型与静止目标一致。通过对累加一维距离像利用最小熵准则求线性相位差异的方法作改进，在保证精度的前提下，有效地降低了计算量。补偿线性相位差异后，构造表征各雷达回波相参性的相关系数，全局搜索求固定相位差异。最后通过仿真对比说明了本文方法的优越性。

1 动目标幅相差异模型

单部雷达对动目标相参测量不存在问题，但是不同频段独立工作的几部雷达在邻近配置时，对同一动目标观测却面临着速度、布站、起始载频、时间等的差异带来的非相参[11-12]，必须将其补偿。由于幅度差异可以作归一化补偿，因此本文重点分析相位差异。

以两部雷达为例说明，多部雷达情形可类推。以最常用的线性调频体制为例分析，假设两雷达的调频斜率K相等，f1,f2是载频的起始频率，Δ是两雷达的钟差，t1,t2是两雷达开始测量的时刻。对含有Q个散射中心且与雷达径向距离分别为R1i,R2i的拓展平动目标而言，由于不同散射中心的速度只与观测角度有关，当两雷达观测角度相差不大即邻近配置时，可近似认为各散射中心径向速度相同，此处设为v。对两雷达回波进行Dechirp处理[13]，不失一般性假设参考时延为0，文献[14]中已详细分析了如何补偿Dechirp后的视频相位项，故本文暂不考虑：

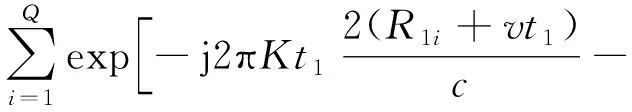
(1)

(2)

以上两式可以再写为

(3)

(4)

令t2=t1+δt，由以上两式可知两异源雷达的相位差异为

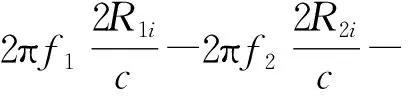
(5)

从上式中可以发现，动目标相位非相参因子分为线性、固定相位差异，其中前3个和式是固定相位差异，包含载频差、距离差以及时刻差和钟差造成的动目标距离延时和多普勒延时；后4个和式是线性相位差异，包含两雷达时刻差、钟差、多普勒差、距离差造成的时延项。

而静目标非相参量为

(6)

静目标非相参量中前3个和式是固定相位差异，包含载频差、距离差以及时刻差和钟差造成的静目标距离延时；第4个和式是线性相位差异，包含雷达距离差造成的时延项。可见动目标的非相参量在形式上与静目标一致。可以参照静目标相参配准方法处理。但是由于相参配准只是以某部雷达为参考，将两部雷达相位校准，在动目标情形中配准后两雷达依然具有速度。如果考虑到回波幅度随频率的衰减，则雷达1的几何绕射理论(Geometrical Theory of Diffraction, GTD)模型为

(7)

(8)

式中：

(9)

(10)

可见上式中DE模型的幅度和极点都是变量，无法利用DE模型参数估计类方法进行带宽外推，因此还需要先进行速度补偿，其位置在相参配准前后均可。本文在相参配准前补偿速度，这是由于补偿速度后的残余误差可以在相参配准时进一步补偿，有利于整体相位补偿效果。

2 速度补偿

观察式(3)、式(4)可知，分别在子带估计速度后，利用式(11)在各子带补偿速度，剩余非相参因子与静目标相同，求解方法可参照静目标相参配准方法。此外，由式(5)可知,残余速度引起的残余非相参量会体现在线性、固定相位差异上，可以进一步在后续相参配准中补偿。

(11)

在各子带对目标速度的测量采用MTD方法。以雷达1测量单散射中心为例，雷达2及多散射中心情形可类推，式(12)是Dechirp后的表达式，R0是最初的径向距离，n′=0,1,2，…是脉冲数(第n′+1个脉冲)，t1∈[0,T1]：

(12)

上式中第二个指数项为视频相位项可以进行补偿[14]，在接下来的推导中暂时忽略，则

(13)

exp(j2πKt1τ′-j2πfd1t1-j2πf1τ′)

(14)

(15)

则最大模糊速度为

(16)

将上式Δvdmax替代式(3)中的v：

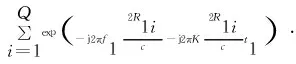
(17)

则由最大模糊速度引起的相位误差为

(18)

上式最大值是当t1=T1时：

(19)

当相对带宽不大时，上式较小,可忽略。因此MTD求得的模糊速度就可以代入式(11)进行速度补偿，剩余非相参量就是静止目标的非相参因子。

对本文方法补偿速度的效果评价，采用在各子带补偿速度后，由残余速度Δv引起的残余项，利用其相位的大小评价本文方法的补偿效果，如式(20)所示：

(20)

3 相参配准

文献[9](记为R方法)与文献[8](记为E方法)提出的线性相位差异求解方法都是十分优秀的算法，从根本上讲，都是利用了存在线性相位差异的两异源雷达一维像间的平移量。如图1所示是在0～20 dB信噪比下，每隔2 dB做100次蒙特卡罗实验，在相同条件和参数下两种方法的精度和计算量对比，可见E方法在低信噪比下精度较高，而8 dB以上信噪比两方法的精度一致。但E方法计算量却远远大于R方法。本文将对文献[8]的方法作改进，在保证其精度前提下，大大降低计算量。

由文献[7]研究可知,熵可以衡量图像的锐化程度，熵值越小图像越尖锐。而研究表明,两异源雷达之间存在线性相位差异主要表现为对同一目标观测的一维像之间有一个平移量[15]。如果平移一个一维像并与另一一维像叠加，则叠加后熵值最小时图像最尖锐，即两一维像刚好对齐，利用该平移量就可求出线性相位差异。

由前文分析可知，式(3)、式(4)所示的两雷达的动目标回波在各子带补偿速度后，剩余非相参量与静目标一致。两雷达静目标GTD模型可写为如下形式：

(21)

x2(t1)=x1(t1)exp(jt1η2+jη1)

(22)

式中：

(23)

对式(22)时域离散采样后，n是时域采样点[16-17]：

x2(n)=x1(n)exp(jη1)exp(jnη2)

n=0,1,…,N-1

(24)

对上式作离散逆傅里叶变换得

(25)

(26)

(27)

但是该方法在搜索熵的最小值时，遍历了所有采样点，计算量较大。本文提出先确定一搜索范围，再在其内搜索熵的最小值，在保证精度的前提下，大大降低了计算量。图2是在4 dB信噪比下，两个带宽都为200 MHz，起始载频分别为24.0 GHz和24.4 GHz，存在exp(jt·π/11)的线性相位差异的高低子带雷达，对间距为0.5 m和1 m的3个散射中心所成一维像。由图2可见，由于线性相位差异的存在，使两雷达一维距离像有个平移量，如果直接将这一平移量作为搜索熵最小值的平移量，可能会由于两一维像峰值对应的散射中心不匹配，导致搜索熵最小值错误。因此本文提出对两一维像所有采样点求均值，分别在两一维像峰值两侧搜索第一个比均值小的采样点位置p1l,p1r,p2l,p2r，则在p2r-p1l+1的平移量之内搜索累加一维像后图像熵的最小值对应的平移量，再利用式(27)求线性相位差异。

为了估计固定相位差异，构造如下表征两子带相参性的相关系数，r(ξ,ζ)表示求ξ和ζ的互相关系数：

(28)

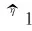
(29)

4 算法处理流程

图3是本文方法的流程图，下面简要总结本文方法的步骤：

1)对两雷达分别Dechirp处理，并作MTD求出两雷达量测的速度，利用式(11)在子带上分别补偿速度；

2)对两雷达回波成一维像，分别在两一维像峰值两侧搜索第一个比均值小的采样点位置p1l,p1r,p2l,p2r；

3)在p2r-p1l+1的平移量之内搜索累加一维像后图像熵的最小值对应的平移量，用式(27)求线性相位差异并补偿；

5)利用矩阵束方法建立全局DE模型[19-20]，“填补”空缺频带；

6)对全局DE模型作FFT成一维像。

5 仿真实验验证

仿真实验中，采用如式(30)所示的GTD模型作为静目标理论全频段数据：

(30)

式中，起始载频f1=20 GHz，k=B/T,而带宽B=300 MHz，时宽T=0.06 ms，用2.56 MHz的采样率对式(30)进行采样。由于B/f1≪1，上式可以近似为DE模型[16]，可以用矩阵束方法由两子带得到全频段DE模型。两子带雷达数据如式(31)、式(32)所示：

(31)

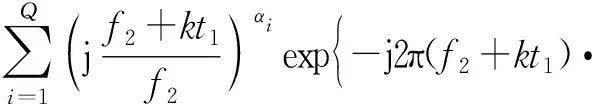
(32)

在0 dB信噪比下，以式(20)的相位值来评价补偿速度的效果。仿真结果如图4所示，易见残余速度Δv引起的残余项极小，且残余量可以进一步在后续相参配准中补偿。

图5是在0～20 dB信噪比下，每隔2 dB做100次蒙特卡罗实验，逆傅里叶变换点数为1 024，对文献[7]方法(记为A方法)与本文对其改进后(记为B方法)的精度和运算时间的对比图。由图5可见，经改进后既保证了精度，又大大降低了计算量。其中改进后计算量随信噪比增加而略有增加，这是由于信噪比高时一维像峰值两侧第一次小于均值的点距离峰值越远，搜索熵的最小值所用采样点越多，计算量稍有增大，但是每个信噪比下，计算量都远远小于A方法。

构造本文提出的相关系数，在0～20 dB信噪比下，每隔2 dB做100次蒙特卡罗实验，按步长0.001在[0，2π]内全局搜索固定相位差异。结果如图6所示，在0～20 dB信噪比下均方根误差都在10-2rad量级，精度很高。

按照本文整体算法流程及步骤，对两异源雷达观测同一动目标进行相参合成，结果如下所示。图7、图8分别是无噪和信噪比为8 dB时时域和一维距离像对比，由图7(a)、图8(a)可见，经过带宽合成后距离分辨率显著提高，且由图8(a)可见，在8 dB信噪比时，只是幅度稍有变化，位置依然准确，算法对噪声不敏感；由图7(b)可见，无噪时带宽合成后时域波形与理论时域波形大多采样点都吻合较好，由图8(b)可见在8 dB信噪比时，由于噪声导致两者幅度有所差异，但是时域波形没有太大时移。

6 结束语

本文对较少研究的动目标异源雷达带宽相参合成问题进行了研究。通过分析动目标幅相差异模型，直接在子带估计并补偿目标速度，剩余的相位差异与静目标相同。通过对累加一维距离像利用最小熵准则求线性相位差异的方法作改进，在保证精度的前提下，有效地降低了计算量。补偿线性相位差异后，建立只含有固定相位差异的表征异源雷达相参性的相关系数，通过全局搜索估计固定相位差异。最后通过仿真对比说明了本文算法的有效性。