CT系统参数标定的研究

文/张文佳

1　引言

CT 可以在不破坏样品的情况下，利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像，由此获取样品内部的结构信息。在图像信息充斥的现代，CT系统安装时往往存在误差，从而影响成像质量。故借助于已知结构的样品对安装好的CT系统进行参数标定，并据此对未知结构的样品进行成像，已成为现代科学研究的重要课题。

然而CT参数的求解方法更是多种多样,难以分辨出优劣。如文献[2,3,5]在求解探测器间距时都是认为存在经过圆形模板中心的射线,而事实并非如此。文献[2～4]在求解旋转中心时,都是通过直接数非零单元格个数来求解的,而没有将椭圆模板和圆形模板进行分离,这样计算精度较低。本文综合这几方面的缺点对模型进行了改进,减小了误差,具有推广意义。

2　CT系统参数模型的建立与求解

对于求解探测器间距,椭圆形样本和圆形样本都可以采用。一种比较粗糙的方法是数数据中非零值的单元格个数,但是由于可能不存在通过椭圆样本或圆形样本中心的射线,所以这种方法误差较大,故我们将采用另一种精确的方法来计算探测器间距。对于求解旋转中心的坐标,我们把椭圆样本数据和圆形样本数据进行了分离,进而比较精确的求就出了旋转中心的坐标。

2.1　探测器间距模型的建立与求解

2.1.1模型的建立

表1　

对于求解探测器间距,我们不确定是否有射线穿过样本的中心,因此我们随机取了圆形样本一列部分非零数据进行分析,数据如表1所示。

从表1中我们可以看到圆形样本的衰减并不对称,因此可以确定不存在通过圆形样本中心的射线。

根据X射线衰减的性质知：当一束强度为I的X光通过厚度为dx的吸收体后,强度减少量-dl近似正比于dx乘积。因此我们以X光的衰减量作为X射线通过圆形样板的公称弦长,近而此时圆形样板的半径称为公称半径,探测器间距称为公称间距。从而求解出公称半径rnr和公称间距dnd,而rnr和dnd与实际半径rreal和实际间距dreal成正比,其比例系数为μ,也称为衰减系数。

根据分析可以得到如下方程组：

其中a,b,c,d为同一列数据中的衰减值，∆1,∆2为探测器编号之差。

为了减小误差及简化计算，我们对方程组（1）进行简化（令a=c）得到方程组（2）：

2.1.2模型的求解

我们从表1，EB列中取a,b,d的值分别为：3.5705，14.1796，3.4752,进而求的结果为：

可以知道圆形样板实际半径rreal=4，可求得衰减系数μ为：

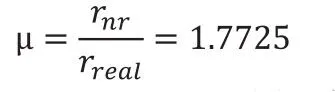
据此可以求得探测器实际间距dreal为：

2.2　旋转中心模型的建立与求解

2.2.1当X射线平行于y轴时

用软件求出数据中非零值最多的列，记为jmax。求出第jmax列中非零值的行，记为Rmax。

则纵坐标y0为：

求解得：jmax=58，Rmax从第92行至380行，y0=5.5363mm

2.2.2当X射线平行于x轴时

当X射线平行于x轴时，首先用软件求出数据中非零值最多的列，记为jmin。然后采用粗略的方法排除小圆的干扰。最后求出第jmin列中非零值的行，记为Rmin。

则纵坐标x0为：

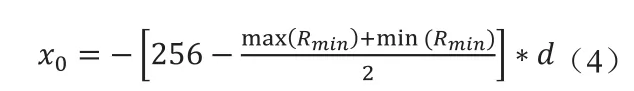
求解得：jmin=150，Rmin从第169行至276行，x0=-9.2734mm

所以旋转中心C的坐标为（-9.2734，5.5363）。

3　结论

本文采用较精确的方法求出了CT系统的相关参数。特别在求解探测器间距时,找出了不存在射线穿过模板中心的事实,精确度大大提到,并且具有推广性。但在分离小圆造成的影响时,因为计算的复杂性没有采用更加精确的方法,故产生了一定的误差。然而最终求解结果与实际参数相差不大,仍然具有实际意义。