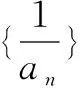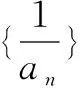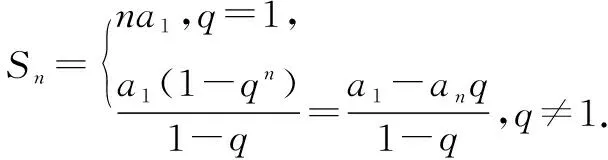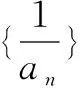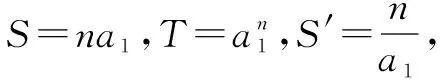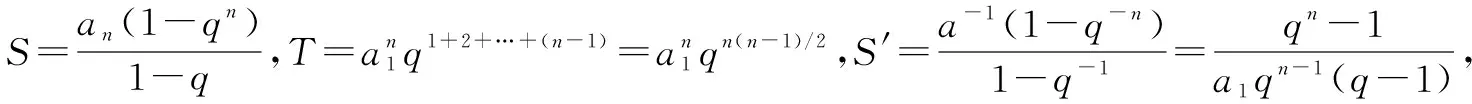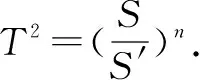关于数学思维困惑成因及常见错解初探

于炳友

(江苏省泗洪县洪翔中学　223900)

新课改的实施使我们的课堂教学发生了很大的变化：教师由单纯的知识传授者变为教学活动的组织与管理者，变为了学生探索知识的引导者和合作者.在实际高中数学教学过程中，我们经常听到学生反映上课时听老师讲课，听得很“明白”，但到自己解题时，总感到困难重重，无从入手；也就是学生私下里讲的“一听就懂，一看就会，一做就错”.有时在课堂上待我们把某一问题分析完时，常常看到学生拍脑袋：“唉，这个题目也不难做么，差一点就做对了！”事实上，有不少问题的解答，是其思维形式或结果与具体问题的解决存在着差异，学困生长期的模仿使其解题时的思维缺乏创造性.学生往往用刚刚入门的数学知识去寻找数学的美感，而其数学基础知识积累量又不够，数学里的逻辑美又寻找不到，这时学生的数学学习兴趣就会逐渐丧失，学生会产生巨大的心理落差，甚至对数学学习有恐惧感.他们常用一句话概括了自己现在乃至今后的数学水平，“我数学总也学不好啊！”而不去寻找学不好的原因，究竟是哪个章节，哪个知识点学的不好.因此，研究学困生的数学思维困惑对于数学教学是十分必要的.

一、高中学困生数学思维困惑的成因

我们知道，数学思维是指人用头脑进行逻辑推导的属性、能力和过程，它反映的是数学的本质及思维规律性.而学困生数学思维，同样是指学生在对高中数学感性认识的基础上，运用分析，归纳思维的基本方法，理解并掌握高中数学内容而且能对具体的数学问题进行论证与判断，从而获得对高中数学知识本质和规律的认识能力.学困生的数学解题思维存在着困惑，这种解题思维的困惑的成因，一部分是由于我们教学中的疏漏，但更多的则来自于学生自身的思维品质的欠缺，长期简单机械模仿，使知识结构和思维模式不成体系.

也就是说，如果教师的教学脱离学生的基础，只顾自我欣赏，在我陶醉；如果学生在学习数学过程中，其新旧数学知识不能顺利衔接，只顾抄记笔记，不去总结.那么这时就势必会造成学生对所学知识认知上的不足、理解上的偏颇，从而在解决具体问题时就会产生数学解题思维困惑，影响学生解题能力.

二、学困生的错解案例

由于学困生数学思维障碍产生的原因各不相同，导致他们数学思维障碍的表现各异，具体的可以概括为：

1.数学思维肤浅，忽略隐含条件：由于学困生在学习数学的过程中，对一些数学基本概念的发生、推理过程没有深刻的体会，而是仅仅停留在表象的概括上，他们多数不能脱离具体表象而形成抽象的思维，自然也无法摆脱局部事实的片面性，不能把握事物的本质.如在苏教版必修五解三角形教学时出现了以下错解案例:

案例1在△ABC中，三边的长为连续的自然数，且最大角为钝角，求这个三角形的三边的长．

错解设a=k，b=k+1，c=k+2(其中k∈N*)，由题意知cosC<0.

由余弦定理得a2+b2-c2<0，

即k2+(k+1)2-(k+2)2<0.

∴k2-2k-3<0，解得-1

又∵k∈N*，∴k=1或k=2.

当k=1时，三边长分别为1,2,3；

当k=2时，三边长分别为2,3,4.

∴这个三角形的三边的长分别为1, 2,3或2,3,4.

错因分析由于三边的长为连续的自然数，所以三边长分别用k，k+1，k+2(k∈N*)来表示，但解题时忽略了k，k+1，k+2能否构成三角形，只考虑到大边对大角，用余弦定理求解，从而产生错误．

防范措施在三角形中隐含条件较多，可能会因为不用心而导致错误，在利用余弦定理求三角形的三边时，先要判断一下三边能否构成三角形．

正解设a=k，b=k+1，c=k+2(k∈N*)．

由a+b>c，知k+(k+1)>k+2，

即k+1>2，得k>1.①

由cosC<0，得a2+b2-c2<0，即k2-2k-3<0.

解得-1

由①②知1

∴k=2，∴a=2，b=3，c=4，

∴这个三角形的三边的长分别为2,3,4.

2．缺乏足够的数学思维能力，不会分类讨论.解决数学问题常常不能抓住题目的本质，不能转化为已知的数学模型或过程去分析解决.在学习苏教版必修五数列教学时出现了如下错解案例：

错因分析由题设无法判断q与1的关系，以上证法，漏掉了公比q=1的情形，故导致错误．

当q=1时，此类数列为常数列(各项均不为0)，其前n项和为na1，故解决此类问题时要细心.一般来说，只要题目中含有字母，就有可能要讨论，否则容易漏解．

由此可见，学困生数学思维障碍及解题困惑的形成，不仅不利于学生数学思维的进一步发展，而且也不利于学生解决数学问题能力的提高.所以，在平时的数学教学中注重突破学生的数学思维障碍就显得尤为重要.

“书越来越难教,高中数学更难教”，这是我和部分同事的感慨.怎样才能避免在课堂上唱独角戏？怎样才能激发学困生的数学学习兴趣？怎样改变很多教师“求学生学”、“哄学生学”的现状？怎样才能真正地让学生做到踏实“求学”？其实，只要我们坚持以学生为主体，了解学困生的学习特点、思维特点，了解他们的学习习惯，以培养他们的数学思维发展为目标，则势必会提升高中数学教学质量，摆脱题海战术，狠抓基础，真正减轻学困生学习数学的心理负担，从而为提高学困生的整体素质做出我们数学教师应有的贡献.各位同仁，素质教育已经向我们传统的高中数学教学提出了更高的要求，而学困生的数学教学也是素质教育的一种体现，只有一线数学教师不断的摸索，对学困生因材施教，才能逐步解决他们数学的学习困惑.以上是我在的数学教学的一点粗浅的认识，希望能得到各位老师们的指点和建议.