净举力及常规可控气象要素对探空高度的影响研究

郭凤娟，王　曼，贾新军

（1.克拉玛依气象局，新疆 克拉玛依 834000；2.新疆兴农网信息中心，新疆 乌鲁木齐 830002；3.洛浦县气象局，新疆 和田 848200）

探空气球施放高度是高空气象观测业务质量考核的一项重要指标，它的高低对探空质量起着至关重要的作用。提高气球的升空高度，意味着可收集到更多更全面的高空气象情报，从而为精细化天气预报、气候监测及相关科学研究提供更加精确的高空气象观测资料。近年来，随着L波段高空气象观测系统、新型雷达等新型高空气象观测系统在全国各地气象站陆续投入使用，中国气象局对探空气球施放高度考核的要求也越来越高，以非GCOS探空站为例，探空平均高度考核的达标标准已经从最初的25 km提高到了目前的28.6 km，提高了3.6 km。因此，加强对提高气球施放高度方法的研究，对于改善和提高我站探空业务质量具有十分重要的现实意义。

文献[1-4]列举了所有可能影响探空高度的因素，并从定性的角度指出了选择合适的净举力对提高探空高度的重要性；文献[5-16]则在研究中结合实际资料，进一步明确了根据不同的天气和季节选择合适的净举力是提高探空高度的关键，并根据多年的工作经验，大致给出了不同季节和天气下的净举力取值范围，但没有对风向、风速、温度、气压、湿度、降水量等常规可控气象要素如何影响探空施放高度进行研究。本课题通过构建多元线性回归数学模型，首次从定量角度研究了探空高度与净举力及常规可控气象要素之间的关系，给出了不同天气条件和季节下可使气球探空高度达到理想高度的净举力合适取值区间，从而为高空气象的观测研究提供了坚实的实践基础。

1　2011—2016年探空高度变化分析

对2011—2016年以来的放球数据进行了整理，分别从07时年平均探空高度、19时年平均探空高度、全年平均探空高度3个层面重点分析了克拉玛依探空气球施放平均高度的基本规律，以期对克拉玛依近年来的探空情况有个整体了解，具体分析结果见图1。

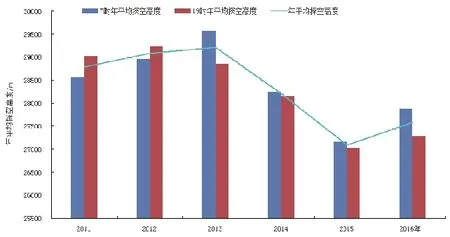
图1　2011—2016年克拉玛依国家基本气象站年平均探空高度变化

从2011—2016年这6 a时间里的年平均探空高度变化图来看，大致变化趋势为：先是逐年缓慢上升，达到顶峰后，又急剧下降，触底后又快速上升。具体来说，2011—2013年这3 a年平均探空高度逐年缓慢上升，均超过了28 600 m，在2013年年平均探空高度达到顶峰，达到29 208.5 m；从2013—2015年这3 a年平均探空高度呈逐年快速下降趋势，2015年达到最低谷，年平均探空高度仅为27 092.31 m；从2015年后，年平均探空高度又快速反弹，呈良好的上升趋势。年平均最高探空高度最高与最低相差约2100 m，07时放球的年平均探空高度变化与年平均探空高度变化趋势大致一致，19时的年平均探空高度与上述两种情况的变化趋势略有不同，2013年19时放球年平均探空高度低于2012年19时的年平均探空高度，而2013年07时的年平均探空高度达到顶峰，为29 565.52 m，明显高于2012年07时的年平均探空高度。由此可见，2013—2015年克拉玛依年平均放球高度呈现整体下降趋势，因此，加强相关研究非常必要且具有十分现实的意义。

2　多元线性回归模型

2.1　模型构建流程

首先筛选出所有可能影响探空高度的因素，并从中选取可控气象要素进行分类，其次从观测数据中选择样本数据，利用处理后的样本数据进行模型初次构建，在此基础上，对模型进行检验和优化。另外，还可以根据选取及分类的因素，扩大样本数据范围，对模型进行进一步的检验和优化，最终确定最优的模型，得出主要影响因素的最佳取值范围。构建流程见图2。

2.2　模型基本原理

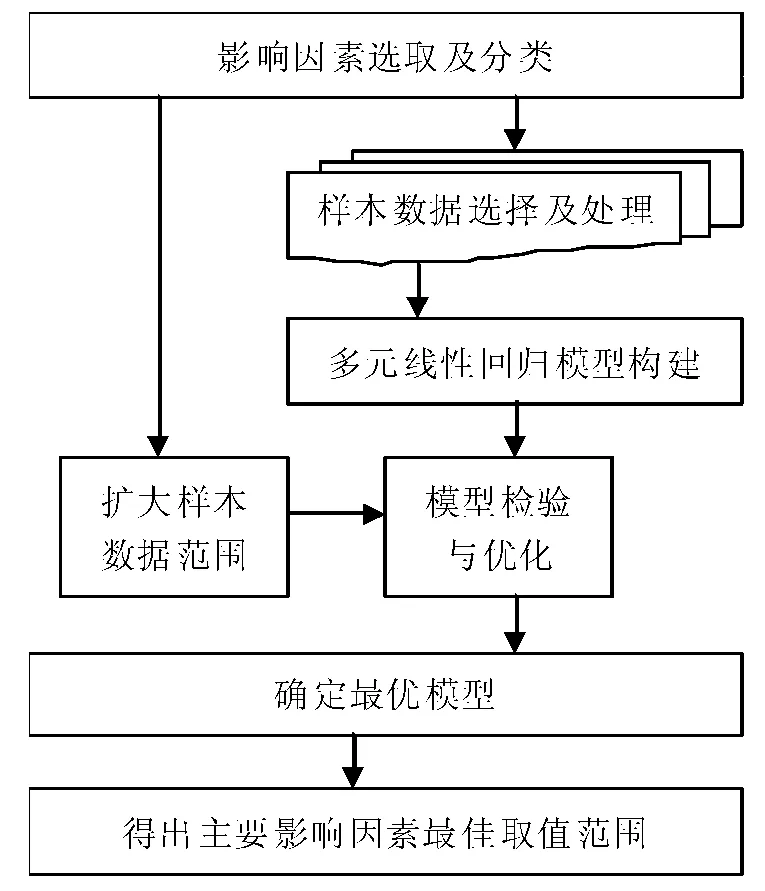
图2　多元线性回归模型构建流程

多元线性回归模型的基本原理是研究一个因变量与两个或两个以上的自变量之间相关关系。给定一个输入向量=（x1，x2，...，xp），若期望预测输出值 f，则线性回归模型的一般形式可以表示为：

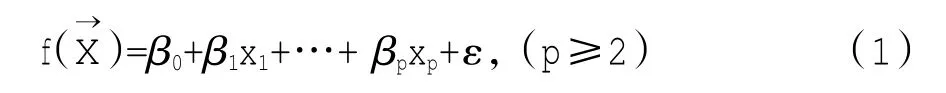
典型地，如果获得n组观测数据（xi1，xi2，...，xip；yi），其中i=1,2,...n。则上述公式可以表示为：

3　实验设计

3.1　样本数据来源

本课题所用样本原始数据来源于克拉玛依国家基本气象站2011年1月—2017年4月750 g气象气球实际观测资料，累计4628次放球数据，剔除13时加密观测数据、20时重放球数据、00时及01时测试数据，选择07时和19时观测记录共计4564条数据作为有效研究数据。选取2016年4月28日至2017年4月28日共计一年的数据作为测试样本着重研究净举力与常规可控气象要素对探空高度的影响。

3.2　影响因素选取及分类

影响探空高度的因素很多，比如气球本身的质量、气球的充灌程序、氢气的纯度、天气状况、净举力控制等，这些因素都对探空气球的施放高度有不同程度的影响。根据长期从事探空工作且经验丰富专家的建议和查阅大量研究文献，最终选取净举力及天气现象、风向、风速、温度、气压、湿度、降水量等常规可控气象要素作为本文研究的重点。

3.3　模型构建

为方便多元线性回归模型构建，需将天气现象用数字化表示，具体来说，数字1代表晴天，2代表小雨，3代表阵雨，4代表大雨，5代表小雪，6代表大雪，7代表10 m/s以上的风，8代表晴天同时伴有10 m/s的风，9代表小雨同时伴有10 m/s的风，10代表阵雨同时伴有10 m/s的风，11代表大雨同时伴有10 m/s的风，12代表小雪同时伴有10 m/s的风，13代表大雪同时伴有10 m/s的风，14代表雾霾天气。

对已有的732条数据进行清理，去除有缺失的数据12条，然后将数据分成两类，60%数据用于模型构建，剩余40%数据用于模型预测与验证，即利用432条数据构建多元线性回归方程，剩余288条数据用于对探空高度进行预测分析。选择8个影响因素作为模型自变量参数，选择IBM SPSS Statistics 19.0软件中的“进入法”得到如下回归方程：

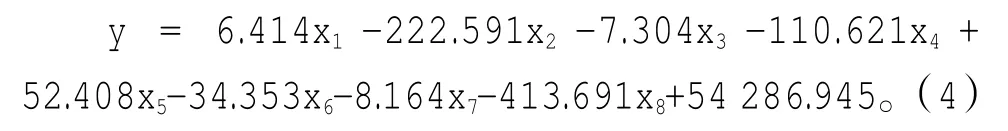
其中，x1代表净举力，x2代表天气现象，x3代表风向，x4代表风速，x5代表温度，x6代表气压，x7代表湿度，x8代表降水量。由上述方程可以看出，净举力、温度与探空高度呈现正相关关系，天气现象、风向、风速、气压、湿度、降水量与探空高度呈现负相关关系，其中天气现象与降水量对探空高度影响最明显。

3.4　模型检验及优化

3.4.1多重共线性检验

多重共线性检验是为了判断自变量之间是否存在相关关系，方差膨胀因子VIF和容忍度是多重共线性检验的两个重要指标，x1、x2、x3、x4、x5、x6、x7、x8的方 差 膨 胀 因 子 分 别 是 8.874、3.267、4.818、2.346、3.787、9.124、6.372和5.118，均＜10，且容忍度均＞0.1，因此，可以判断上述8个自变量之间不存在多重共线性的问题。

3.4.2模型异方差检验

异方差检验主要是为了解决所构造模型是否存在自相关性的问题。数据质量较差和模型设定不合理往往会带来异方差问题，该问题直接导致回归系数估计结果误差较大及模型预测不准确等问题。一般通过残差图来判断模型的异方差的问题。对模型构建数据进行残差分析，得到图3。

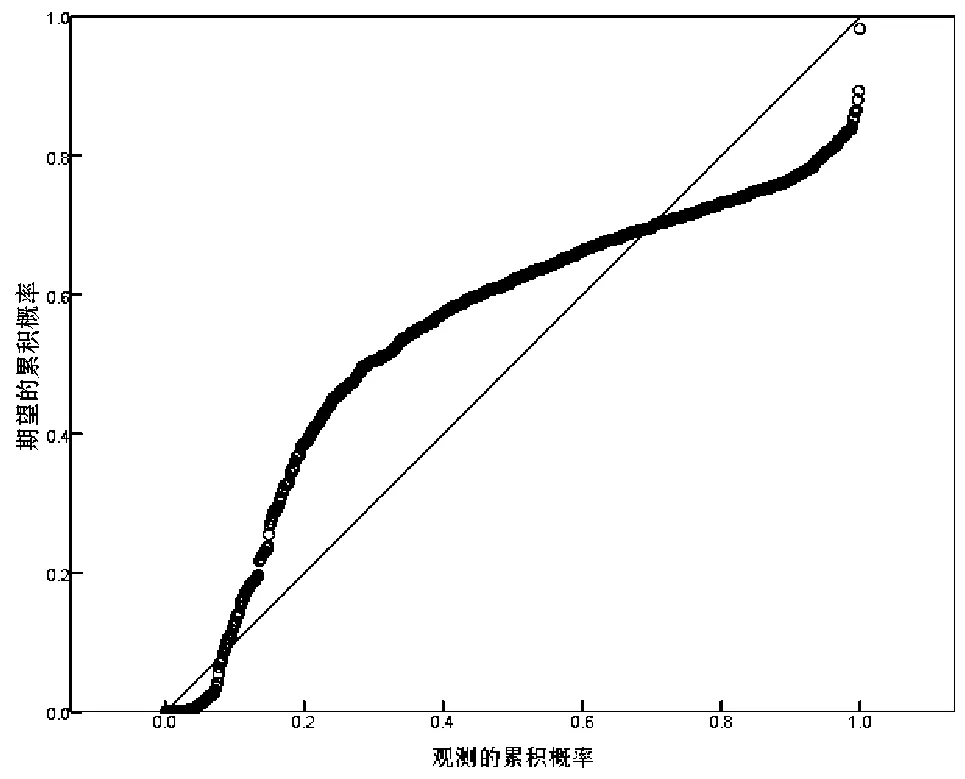
图3　回归方程标准化残差

由图3可知，残差数据大致分布在标准差数据两侧，满足随机分布特性，因此模型本身也不存在自相关性问题。

3.4.3模型优化

通过计算Cook距离，发现部分数据偏离标准偏差较大，即存在所谓的离群点，采用逐步回归的方式逐一剔除这些异常的离群数据，对模型进行进一步优化完善，得到如下回归方程：

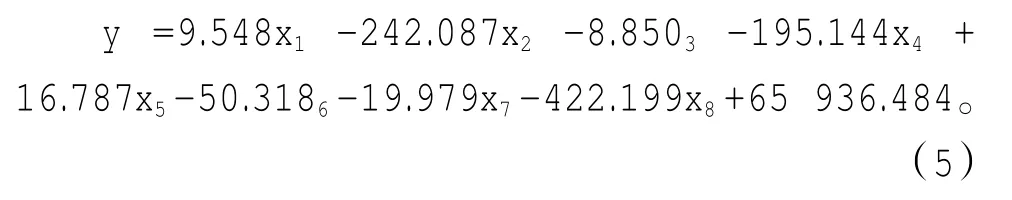
经过优化，回归方程的拟合优度由0.778提高到0.881，说明该模型的预测tgr效果更佳，经反复优化完善，最终确定该模型为最优拟合模型。最优模型异方差检验图见图4。

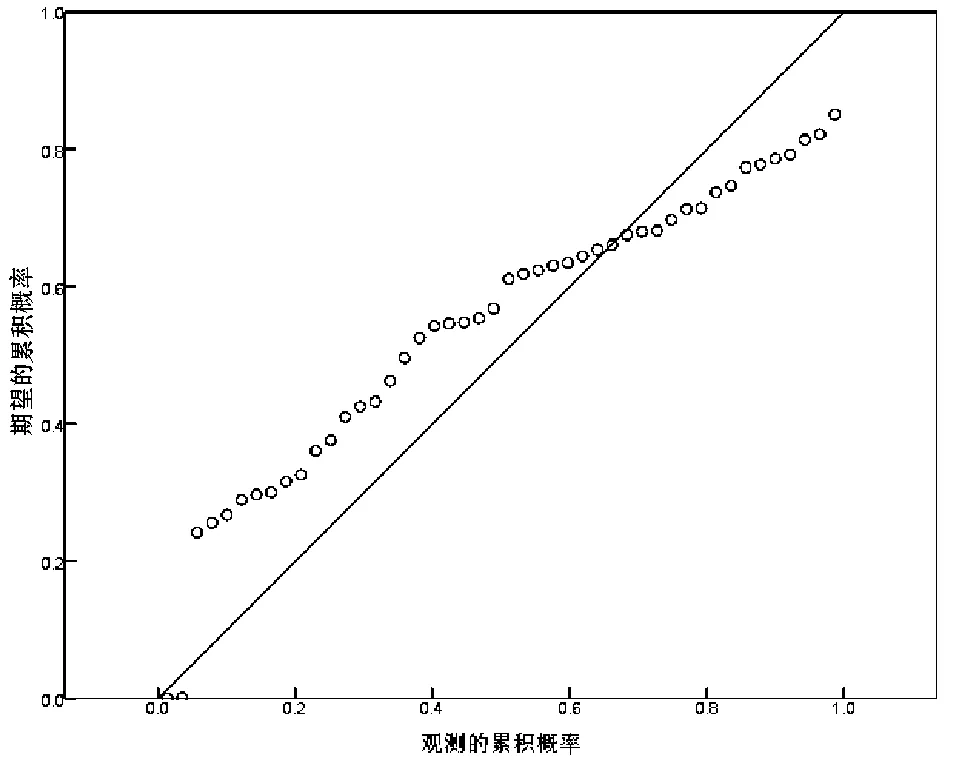
图4　最优模型异方差检验效果图

3.4.4预测效果检验

利用剩余的288条数据对模型进行验证，即将上述两种模型的预测结果与实际值进行对比和验证，经计算，两种模型预测的平均相对误差分别为±8.74%和±8.39%，预测效果较为理想（图5）。

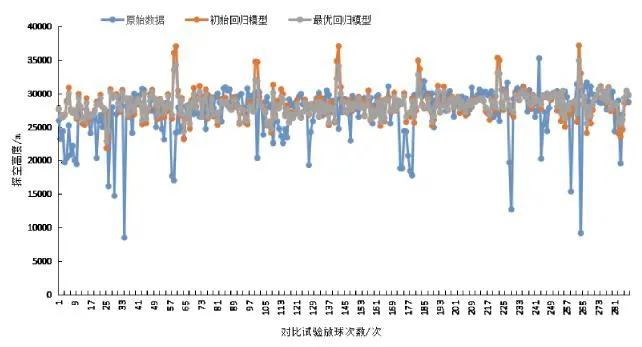
图5　模型预测效果验证

其中，横轴代表288条对比验证放球数据，纵轴代表探空高度，从图5可以看出，最优回归模型验证效果相对初始回归模型预测效果要好。

4　结果及分析

在上述研究的基础上，本文着重探究净举力对探空高度的影响程度，因此绘制了净举力与探空高度关系散点图（图6）。

从图6可以看出，一般情况下，净举力保持在1500～1800 g左右，能以较大概率保证探空气球达到理想的高度；净举力过大或过小都很难再提高释放球高度。

为研究天气现象、净举力与具体天气现象的关系，绘制了3D图（图7）。

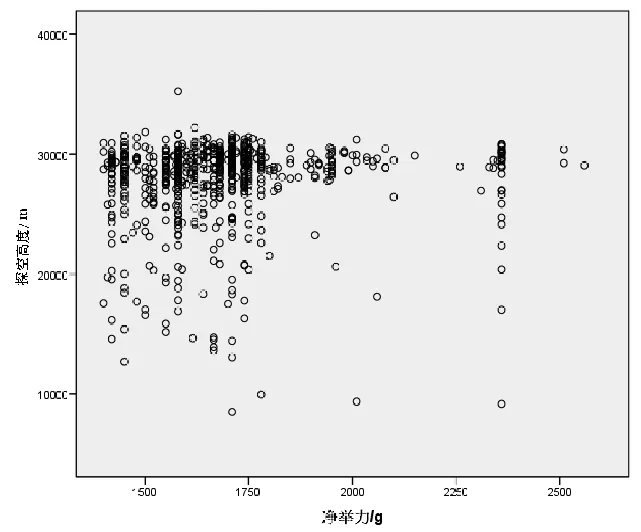
图6　净举力与探空高度关系散点图

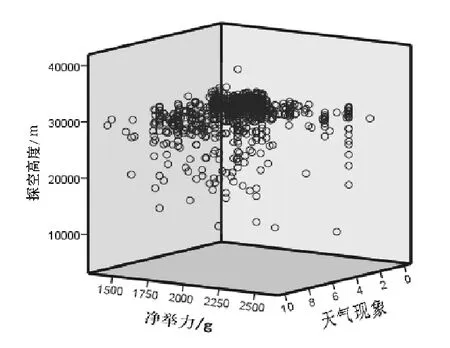
图7　天气现象、净举力与探空高度3D分布

由图7可知，不同天气现象下，探空高度与净举力的关系是不同的。因此，在日常充灌球时要根据具体的天气选择合适的净举力。依据长期从事探空工作专家的建议以及上述统计和分析结果，得出：

（1）克拉玛依四季不是很分明，春季和秋季很短暂，基本上可以忽略不计，大致可以分为夏季和冬季两季。由于温度与探空高度呈现正相关关系，在夏季气温较高时可以适当少充灌些氢，而冬季气温较低时需要适当多充灌些氢气。

（2）晴天或者10 m/s以上的有风天气一般保持净举力在1500～1750 g。

（3）遇到大雨或者大雪天气，净举力要在晴天基础上增加300～500 g，即达到1800～2250 g。

（4）遇到小雨、阵雨、小雪及10 m/s以下的有风天气，净举力保持在1650～1800 g即可。

（5）雾霾天气净举力保持在1650～1750 g即可。

5　结语及讨论

根据中国气象局对探空高度考核指标要求，以及目前国内学者对探空高度影响因素的研究现状，结合2011—2016年6 a平均探空高度变化，从定量的角度构建多元线性回归模型，并对模型进行检验优化和验证实验，确定了最优拟合模型。主要得出以下结论：

净举力与探空高度在某种程度上呈现显著的正相关关系；

在不同季节及天气下选择合适净举力可以适当提高释放球高度。

在研究过程中，未考虑天气现象变化是否在放球时间的情形，比如上午下阵雨，下午19时天气已晴等，即没有细化到放球时间。另外，本文着重讨论了探空释放高度与净举力和天气现象的关系、探空释放高度与气温的关系以及降水量和风速对探空释放高度的影响，而对于气压、湿度、风向对探空释放高度的具体影响没有深入讨论。