利用多测点混合模型对混凝土坝受冻区坝体弹性模量的反演
2018-07-13,,,
, ,,
(河海大学 水利水电学院,南京 210098)
1 研究背景
目前,混凝土的弹性模量一般是通过现场取样,然后通过实验室实测获得,通常是根据实测混凝土强度的平均值确定[1]。而现实情况是现场取样是随机的,并且混凝土的强度分布不同,情况也不相同,因此只用实验均值来确定混凝土弹性模量大小的方法只能确定大坝混凝土强度平均值,不能反映大坝内部真实情况。例如,大坝内部出现受冻破坏时,其受冻区的弹性模量无法确定。除了通过现场取芯试验确定混凝土弹性模量之外,还可以由大坝安全监控混合模型得到,目前国内外监测大坝运行的正反分析仍以单测点监控模型为主[2]。随着科技的进步,除了采用传统方法,许多智能算法也被引入到反分析当中,如改进果蝇算法[3]和量子遗传算法[4]。在研究坝体分区弹性模量反演方面,文献[5]利用改进的模拟退火算法得到了一种反演大坝分区弹性模量的方法。
位于严寒地区的混凝土坝,由于没有及时做好保温措施,甚至有些早期建造的大坝由于施工条件的限制,导致混凝土坝在浇筑过程中受冻,部分混凝土已经受冻破坏。这种情况下,单测点监控模型只能反映测点附近局部变化规律,不能反映大坝每个部位的弹性模量变化情况,对此方面的反演方法研究较少。为了解受冻部位混凝土强度变化,采用多测点混合模型联合反演的方法,引入线性约束优化算法,可以同时对2个或2个以上的测点建立的混合模型进行反演,求得一个使所有参加反演的测点均满足的混合模型,为评价严寒地区大坝坝体受冻区域混凝土强度提供依据,具有实际意义。
2 多测点混合模型联合反演法
假设待反演的坝体Ω,其材料参数属性分布用f(x)(x∈Ω)表示,x是坝体内任意一点,则f(x)可能与很多因素有关,例如x的位置、监测资料的完整性和准确度等。在混合模型中,大坝位移的主要影响因素是水压、温度和时效,即大坝的某点的变形δ可表示为
δ=δH(t)+δT(t)+δθ(t)。
(1)
式中δH(t),δT(t),δθ(t)分别表示位移的水压分量、温度分量和时效分量。
水压分量采用确定性模型,温度分量和时效分量采用统计模型[6]。坝体受冻的位置可通过前期监测资料和施工期的报告大体确定。假设受冻区从坝体上游面贯通至坝体下游面,则坝段混凝土分区分为未受冻区(Ec)、受冻区(Ef)、基岩弹性模量(Er),假设坝体不同高程布置了26个测点,其编号为a—z,图1给出了混凝土分区及测点分布示意图。
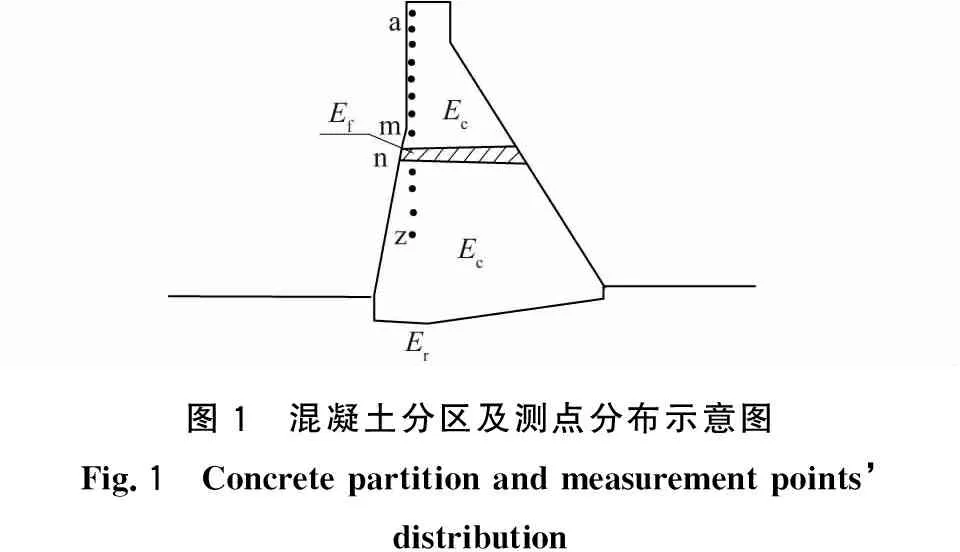
图1 混凝土分区及测点分布示意图Fig.1 Concrete partition and measurement points’ distribution
为了解释模型建立原理,这里选取m测点和n测点(各有i和j个测值)建立多测点混合模型。从图1中可以看出,m和n测点位于受冻区两侧,受冻区弹性模量变化对其值影响不同,因此,用2个测点或者更多的测点建立混合模型,能够提高反演的坝体参数结果的连续性和准确性,减小因单测点而产生的误差。
反演模量主要与水压分量δH有关[7],为了分离水压作用于坝体和坝基变形的影响,采用单因素加载法,分别使水压作用于上游坝面和库底。坝体变形又可分为受冻区变形和非受冻区变形,因此可以分别取基岩、坝体受冻区和坝体未受冻区为弹性体,其余部分为刚体,各种情况下坝体和基岩单独变形组合成观测点的位移。采用这种处理方法在于事先假设一组坝体、基岩的弹性模量,然后结合监测数据使用优化方法对坝体和坝基弹性模量进行修正,以分别反演出坝体、基岩的弹性模量。具体方法如下。
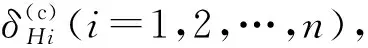
(2)
式中:aci为拟合系数;H为坝前水深;n1为最高幂次数,可取3或4,这里都采用4。
同样的,再分别假设坝体受冻区弹性模量为Ef,其余部分为刚性体,或者基岩弹性模量为Er,其余部分为刚性体,此处公式不再给出。

式中:Xc为坝体混凝土弹性模量调整参数;Xf为坝体受冻区混凝土弹性模量调整参数;Xr为基岩弹性模量调整参数。
为了阐述多测点混合模型建立原理,此处温度分量采用周期项,时效分量采用对数函数和线性函数表示。由式(1)可知,m测点的单测点混合模型为
(4)

同理,n测点的单测点混合模型为
(5)
2个测点联合起来形成多测点混合模型则可写成矩阵的形式如式(6)所示。

(6)
式中:i为m测点的测值个数;j为n测点的测值个数;δ(t1),δ(t2)为温度分量正弦周期项和余弦周期项;δ(θ1),δ(θ2)为时效分量的线性函数项和对数项;δmi为m测点的第i个实测值,δnj为n测点的第j个实测值。
这时,上述问题就转化为求解该方程。当i+j大于未知数的个数,该方程就可以求解。可以看出,当水位在高水位运行时,基岩产生的变形和坝体产生的变形有很强的相关性,这将导致Xc,Xf,Xr存在共线性而影响调整系数的准确性。这时需要对上述调整系数进行估计,通常采用带约束的线性优化问题求解。因此,采用Powell的TOLMIN容错算法[8-9]:利用Wolfe-Powell准则[10]进行非精准线搜索,并通过BFGS公式更新[11],直到迭代满足终止标准。该过程可以通过Fortran程序包IMSL实现。
3 工程实例
3.1 基本资料
某大坝为混凝土宽缝重力坝,修建于1959年,共分为3种坝段:挡水坝段、溢流坝段、中孔泄水坝段,坝段宽度一般为15.0 m。坝基岩石为凝灰集块岩、板岩和后期侵入的玢岩等。反演时选取监控变形资料较为完整、受冻区较为显著的坝段作为典型坝段分析,因此,选取26#和38#坝段分别作为挡水坝段和溢流坝段的典型坝段。
由于横缝的存在,通常认为重力坝各坝段是独立工作的,相互之间没有影响,从而可按平面问题计算坝体变形。计算时取坝基以下以及上、下游方向各取一倍坝高地基。坝段两侧缝宽各3 m。26#坝段共建立单元15 840个,节点18 438个,网格图如图2(a)所示;38#坝段共建立单元23 636个,节点26 768个,网格图如图2(b)所示。
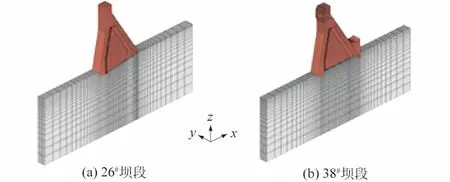
图2 有限元网格模型
本构模型选用线弹性模型计算。基岩弹性模量取25 GPa,泊松比0.26;坝体弹性模量取20 GPa,泊松比0.167;受冻区弹性模量取10 GPa。水荷载仅考虑静水压力,作用在库底和上游坝面,下游水压力和空腔中的水压对坝顶位移影响很小,因此计算时不考虑其影响。
3.2 弹性模量反演
根据上述多测点混合模型反演方法和步骤,利用ABAQUS/Standard有限元软件系统,编制Fortran程序中的线性约束算法优化反演过程,应用于该大坝的坝体受冻区弹性模量反演中。
3.2.1测点的选择
建立各坝段不同测点的水平位移统计回归模型。由表1可知,回归模型拟合结果较好,坝顶测点拟合精度最高,且水压分量占水平位移的比重随测点所在高程增大而增大,其变化符合规律。选择拟合精度较高(统计模型复相关系数R在0.9以上)的坝顶水平位移测点(m)和281高程测点(n)的26#和38#坝段作为挡水坝段、溢流坝段的典型坝段测点进行分析。选择激光观测水平位移监测资料。根据前期资料,初步确定混合模型的弹性模量调整系数未知量有3个,分别是未受冻区弹性模量Ec、受冻区弹性模量Ef、基岩弹性模量Er。
表1模型拟合精度统计
Table1Fittingprecisionofmodels
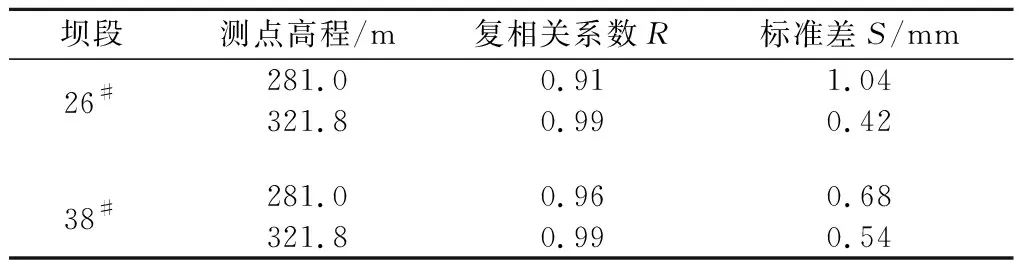
坝段测点高程/m复相关系数R标准差S/mm26#38#281.00.911.04321.80.990.42281.00.960.68 321.80.990.54
受冻区的范围由大坝冬季施工浇筑资料确定。坝体受冻主要是由于施工期没有做好保温措施,因此确定受冻区范围时,参考前期施工监管记录,没有保温措施记录的时间内浇筑的坝体层面视为受冻区。因坝体上下游面受冻情况不同,为了简化计算,选取上下游受冻厚度相同的区域作为受冻区。图3分别为26#和38#坝段测点布置示意图,阴影区为受冻区。
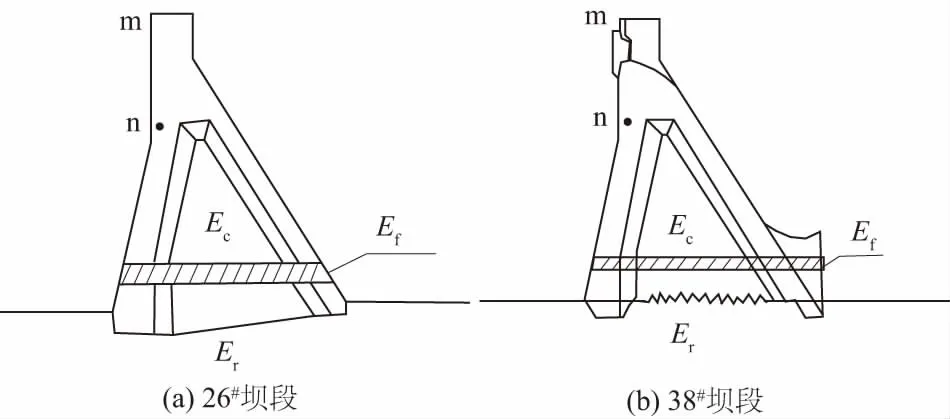
图3 测点布置示意图
3.2.2反演结果
因为坝体未受冻区、受冻区和基岩弹性模量调整系数均有一定的相关性,需要约束Xc,Xf,Xr的范围,这里采取4种约束方法,即:Xc=1, 0 图4(a)给出了38#坝段上述第1种约束条件下,测点混合模型的321.8 m高程测点拟合过程线,图4(b)给出了38#坝段上述第1种约束条件下,281 m高程测点拟合过程线。表2为联合反演法和单测点反演结果的对比,表3为2种反演方法反演结果的拟合精度对比,其中,单测点混合模型选用的是281 m高程测点进行。 图4 38#坝段不同高程测点拟合过程曲线 坝段两点联合反演弹性模量/GPa单测点反演弹性模量/GPa受冻区未受冻区受冻区未受冻区26#7.5023.147.6423.2138#5.5118.365.5118.78 表3 2种反演方法拟合精度对比 从表2结果可以看到,2种反演方法反演出的坝体综合模量基本相同,说明利用多测点混合模型联合反演混凝土大坝受冻区弹性模量的方法是可行的。 因为坝体未受冻区、受冻区和基岩弹性模量调整系数均有一定的相关性,需要约束Xc和Xr的范围:由数值计算结果可知,基岩变形产生的水压分量占总水压分量的比重大概为20%,所以约束基岩弹性模量的调整系数在1左右不会对参数反演带来明显误差;由表2可知,26#和38#坝段坝体综合弹性模量在17~24 GPa之间,因此约束坝体未受冻区弹性模量调整系数在1左右总体也可以接受。 从表3拟合精度可以看出,多测点联合反演模型精度较高。图4中,281 m高程位移拟合精度不高,主要与281 m高程测点本身相对观测精度有关,因表1中,281 m高程单测点的混合模型复相关系数相对两测点联合反演模型较低。 本文利用水平位移监测资料建立多测点混合模型联合反演得到受冻区弹性模量的参考值,反演过程中分离了坝体未受冻区、坝体受冻区及基岩对于测点位移影响,采用优化算法对受冻区混凝土弹性模量进行反演,得出以下结论。 (1)采用Fortran中的线性约束优化算法提高了优化算法的效率,建立的多测点混合模型拟合精度较高,说明该方法是可行的。 (2)本文采用简化的方法确定受冻区范围,即受冻区域上下游贯通且高程方向上厚度相同,但对受冻区分布较复杂的情况则不适用该方法。对于如何确定受冻区范围在上下游方向上未贯通的坝体混凝土弹性模量,有待进一步研究。 (3)用多测点混合模型试探性地计算出大坝受冻区弹性模量的大致范围,可以作为严寒地区早期修建的混凝土大坝运行性态研究的依据。 (4) 多测点混合模型反演坝体受冻区弹性模量的影响因素,除了测点精度和测点空间分布,还有一些非决定性因素,如上游水位。当上游水位均为高水位时,误差较小,因水位越大,位移也越大,整体计算的误差就会相对缩小,但是遇到极高的水位,模型误差反而会增大,具体规律有待进一步研究。


4 结 论
