多产品救援物资的储备决策: 一个扩展的Newsvendor模型
2018-07-13陈敬贤
陈敬贤,梁 樑
(1. 南通大学商学院,江苏 南通 226019;2. 合肥工业大学管理学院, 安徽 合肥 230009)
1 引言
随着人类社会的不断发展进步,灾害事件也在频繁爆发,给社会及人类生命财产安全带来了极大的影响。世界红十字会组织International Federation of Red Cross and Red Crescent Societies (IFRC)2014年年度报告指出,在过去的十年里(2004-2013),世界范围内总共爆发了6525起灾害事件,共有1059072人因灾害事件而丧生,共有19979.32万人受到了灾害事件的影响[1]。而EM-DAT的数据(EM-DAT统计的是有十人以上丧生的灾害事件)则表明2014年中国总共爆发了40起灾害事件,居全世界之首,在灾害中受伤的人数达到6496万人,直接经济损失达到289.5亿美元[2]。这些数据充分表明,研究有效应对灾害事件的方法与策略具有明显的意义和价值。
《中华人民共和国突发事件应对法》将突发事件的应急管理划分为预防与应急准备、监测与预警、应急处置与救援和事后恢复和重建等四个阶段,也有文献将突发事件的应对划分为应急预备、响应和恢复重建等三个阶段[3-5]。本文研究应对灾害事件的物资储备问题,属于应急预备或预防与应急准备阶段的内容。从已经发表的文献来看,目前的研究偏向于关注应急响应问题,而预备、监测与预警及恢复重建等重要问题的研究还较为鲜见。但从救援管理的实践来看,应急预备阶段的工作尤为重要。例如,中央政府在《突发事件应对法》中就强调“突发事件应对工作实行预防为主、预防与应急相结合的原则”。实际的案例也对此进行了说明。例如,以典型救援物资帐篷为例,汶川地震发生后两天,全国10个中央物资储备库中的18万顶帐篷被掏空,而仅为安置四川、陕西和甘肃3省的灾民,就需要300多万顶帐篷,这一事实表明了帐篷的储备在地震发生后表现出明显的不足;而在汶川地震发生以前,我国10个中央储备仓库中尚剩余1998年储备的帐篷约88000多顶,而仅是为维持这些帐篷基本功能的维修费、管理费每年就高达近百万元。这一事实反映出,储备一定数量的救援物资具有明显的必要性,但同时也具备一定的风险性,平衡储备物资的必要性及风险性研究救援物资的储备决策是亟待研究的重要问题,这也是本文研究的主要内容。
本文的研究问题属于应急预备阶段,下面对应急预备阶段的已有相关文献进行综述。关于应急监测预警、应急响应及事后恢复与重建等方面的研究可以详见Altay和Green、Galindo和Batta的综述[7,8]。Whybark、Tomasini和Van Wassenhove的定性研究较早的关注了应急资源的储备与库存问题,他们均指出储备一定数量的救援物资对于提高救灾效果及效率具有重要意义[9,10]。Beamon和Kotleba[11]建立了一种改进的(Q,r)决策模型,并利用该模型确定救援物资的最优订货量和再订货点。Lodree[12]基于minimax准则研究了应对飓风灾害的救援物资的预防性与响应性控制策略。Duran等[13]针对国际救援组织CARE的实际案例,基于整数规划模型研究了救援物资的库存决策。Balick和Ak[14]同样利用数学规划的方法研究了救援组织的供应商选择及库存决策等问题。以上这些研究均是在假设灾害事件发生的基础上,救援组织的如何利用预防性的策略来应对,本质上仍然属于应急响应阶段的物资调度与规划问题。
近年来,渐有学者开始运用报童模型来研究救援物资的库存决策。Lodree和Taskin[15]利用报童模型量化了应对灾害事件的救援物资的最优订货量,并进一步讨论了救援物资储备的保险策略。Chakravarty[16]利用报童模型讨论了救援组织的或有计划,该计划包含了应急预备、响应和恢复重建三个阶段的产能及供应商的批发价决策;进一步,他又在该模型的基础上讨论了灾害事件发生后的快速响应机制[17]。Das和Hanaoka[18]开发了一种估计需求及救援组织期望成本的方法,并在此基础上讨论了救援组织的最优库存决策。Campbell和Jones[19]利用报童模型研究了救灾物资供应商的选址及库存决策,他们同时考虑了供应商在灾害事件中被摧毁的可能。Wang Xihui等[20]研究了救援物资供应链预采购的期权契约及供应链协调。王熹徽和梁樑[21]研究了救援供应链的采购策略及期权契约协调机制;陈涛等[22]研究了应对突发事件的社会化储备体系中,协议企业实物储备、生产能力储备的协调性问题;王熹徽等[23]研究了救灾网络的解构及其优化问题;张琳等[24]研究了基于价格柔性契约的应急物资采购问题。以上文献均是在利用报童模型的基础上开展研究的,但均是针对单一产品的救援物资,并没有考虑多产品的救援物资储备决策。显然,实际救援管理工作中往往牵涉到多种救灾物资的储备决策,这也正是本文研究的主要问题。另外,本文同时也考虑了当储备物资不足以全部满足灾民需求时,救援机构利用社会捐赠物资和(或)应急采购物资来满足需求,而这也是已有文献并没有考虑的,尤其是关于社会捐赠对于救援物资储备的影响。
本文考虑救援实际中需要储备多种救援物资,通过刻画各种灾害事件发生的概率并进一步联系其对应的物资需求情况,建立考虑多种潜在灾害事件的救援物资需求模型,进而研究了物资储备的最优决策。考虑到救援实际中的物资储备常常受到财政预算的限制,本文还研究了具有预算限制的多产品救援物资储备决策模型及其求解算法。本文的主要贡献在于:(1)通过引入多种可能发生的灾害事件集,刻画了救援物资的需求模型,并在此基础上建立了多产品救援物资的库存决策模型;(2)在救援物资需求全部被满足的前提下,提出了一种灾害事件发生后救援物资的二阶段交付过程模型。该模型同时考虑了储备物资和社会捐赠及应急采购物资的交付,为刻画救援组织机构的期望成本奠定了良好的基础;(3)提出了具有预算约束的多产品救援物资储备决策模型与求解算法。
2 模型
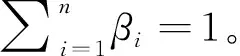
2.1 两阶段交付过程
为了刻画NPO的期望成本函数,本文首先描述灾害事件发生后NPO的交付过程。在对实际救援管理工作进行总结的基础上,本文利用图1对NPO交付救援物资的事件进行描述,并在此基础上勾画了一种救援物资的两阶段交付过程。
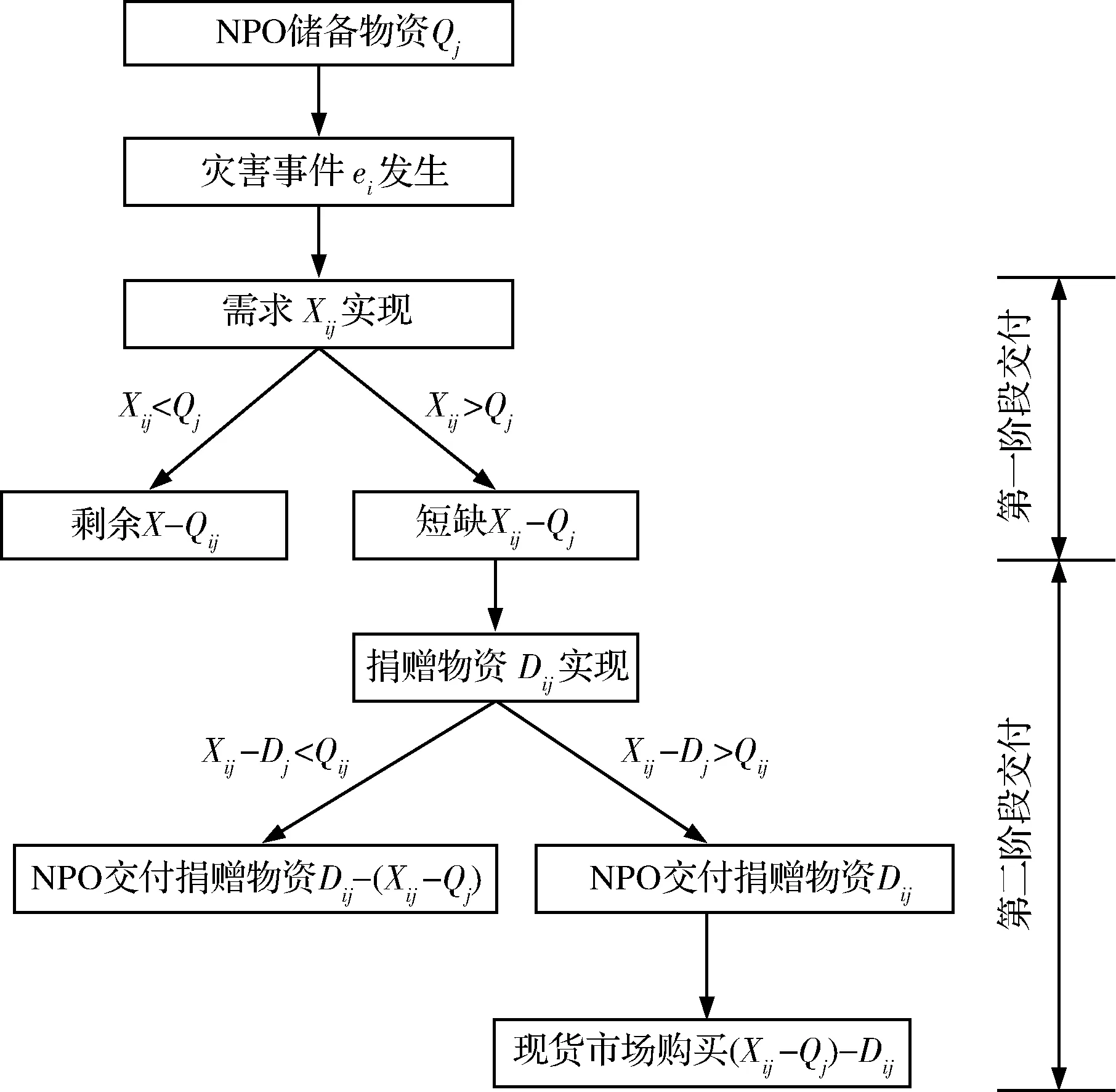
图1 救援物资两阶段交付过程
图1所示的两阶段交付过程的含义是,当灾害事件发生后,NPO首先交付储备物资;如果灾害事件引发的需求大于储备物资数量,即Xij>Qj成立,那么第二阶段的交付开始,其目的在于完全满足剩余需求Xij-Qj。单位短缺需求需要支付惩罚成本pij,这一成本由延迟交付短缺需求引发的社会成本[16-17]。本文这里的两阶段交付过程主要是在对救援管理实际抽象的基础上得到的。例如,2013年4月20日,四川雅安地震7.0级地震爆发以后,非营利组织壹基金在震后的24小时内交付了储备在西安、贵阳、遵义等地救灾仓储的大量的救援物资,剩余的灾民需求也在接下来的一个月里通过综合利用社会捐赠及应急采购而满足[26]。需要说明的是,图1所示的两阶段交付本质上是一种广义的二阶段交付,在实际中可能并不止两次交付,本文这样假设的目的在于区别对待储备物资和应急物资的交付。当然,本文这里的两阶段交付过程也可以拓广至n阶段交付。另外,在管理实际中也有救援主导机构采用储备供应商产能的措施(如协议储备、协议企业生产能力储备)来实现短缺救援物资的储备,本文这里并没有考虑这一问题,而是深入研究捐赠物资对于救援物资储备的影响。关于协议储备及协议企业生产能力储备可以参考文献[22]。

2.2 期望成本函数
根据图1及上文的符号定义,可以得到NPO的期望总成本为
(1)
其中,TC表示NPO的期望总成本;Q表示救援物资的储备数量集,即Q=(Q1,…,Qm);E为期望值算子;符号(·)+≡max(·,0)。
式(1)右边第一项表示的是储备物资的采购成本,第二项表示的是交付储备物资的成本,第三项表示的是储备物资的残值,第四项表示的是短缺需求的惩罚成本,第五项表示的是使用捐赠物资的处理成本与交付成本,第六项表示的是除了使用捐赠物资以外的紧急采购物资的采购与交付成本。
2.3 模型假设
对于本文模型中涉及的相关成本参数,提出如下假设条件:
(2)
式(2)中的第一个条件是表示储备救援物资并不能获利;第二个条件是说明现货市场的单位产品价格大于储备物资的单位采购成本,该条件若不满足,NPO没有储备救援物资的激励。该条件主要源自救援工作的管理实际,文献[6]指出当前我国救援管理工作中最大的困难在于如何“存储价格”,物价上涨已然给救援物资储备带来了极大的困扰。条件pij>tij+cj表示的是交付单位储备物资能获取正的“收益”。这个条件的含义是单位短缺物资的惩罚成本足够大以至于在灾害事件发生后,NPO有激励首先交付储备物资来满足灾民需求,而不是让需求短缺,然后再利用捐赠物资或应急采购物资来满足。最后一个条件是保证NPO有激励首先利用捐赠物资来满足剩余需求。另外本文假设灾民需求失去的惩罚成本为一个足够大的正数,以此来保证NPO有激励满足所有的灾民需求。
3 无约束的多产品储备决策
本节将讨论不存在任何约束时NPO的最优产品储备决策问题。定理1对该问题的最优解进行了描述。

(3)
证明:由于TC(Q)为关于变量组合(Q1,…,Qm)的可分离函数,因此,只需要证明TC(Q)为任意变量Qj的凸函数,即可证明TC(Q)关于(Q1,…,Qm)的联合凸性。求解TC(Q)关于任意产品Qj的二阶偏导数,可以得到
(4)

(5)
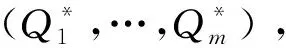
4 具有预算约束的多产品储备决策
实际的救援储备工作中常常存在预算或容量限制。例如,四川成都的中央级救灾储备库总占地面积为158.23亩,总的有效库容为3.7万立方米,拥有近万个货位,可储备帐篷5.41万顶、棉被10.83万床、棉衣裤21.65万套等各类救灾物资和冲锋舟、橡皮艇、救生圈、发电机、挖掘机等各类应急救援工具,可同时满足紧急转移安置人口86.6万、救助21.65万人所急需的救灾物资储存、调运等紧急任务,并能保障两架直升机同时起降。由此可以发现,制定该储备仓库的产品储备决策时,就应该考虑到仓库容量的约束。根据文献[30]可知,在多产品Newsvendor模型中,容量约束与预算约束是完全等价的。本文这里采用预算约束主要是为了避免确定单位产品救援物资所占用的容量比例,而对于预算约束而言,这一比例即为单位产品的采购价格。另外,预算限制的做法在救援实际中也是常见的,例如我国《预算法》第三十二条规定,各级政府预算应当按照本级预算支出额的1%—3%设置预备费,用于当年预算执行中的自然灾害救灾开支及其他难以预见的特殊开支[31]。
假设预算限制为B(B≥0),由此可将NPO的储备决策问题归纳为如下的数学规划问题:
(6)
(7)
Qj≥0,∀j∈{1,…,m}
(8)
其中,式(6)表示NPO的目标函数;式(7)表示物资储备的预算限制;式(8)是储备物资数量的非负性要求。需要说明的是,预算限制主要是针对物资储备决策的,但并不针对灾害事件发生后的应急物资购买。
根据定理1可知,问题(6)—(8)为凸规划,因此Karush-Kuhn-Tucker(KKT)条件为该问题最优解的充分必要条件。式(9)—(12)给出了问题(6)—(8)的KKT条件。
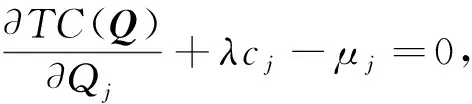
(9)
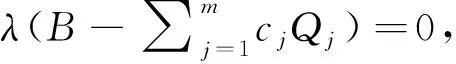
(10)
μjQj=0,∀j∈{1,…,m}
(11)
Qj≥0,∀j∈{1,…,m}
(12)
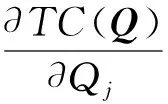
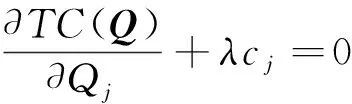
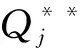
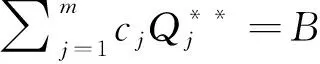
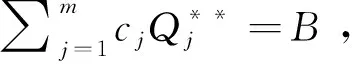
性质2记λ(Qj)为Qj(λ)的反函数,则有:(1)λ(Qj)为关于Qj的减函数;(2)Qj(λ)为关于λ的减函数;(3)λ(Qj)是有界的,满足0≤λ(Qj)≤λmax。其中,λmax由式(13)确定:
λmax=
(13)
λ(Qj)=
由于λ(Qj)为关于Qj的减函数,因此当Qj→0时,λ(Qj)达到最大。将Qj=0代入上式可以得到λ(Qj)的上界λmax。证毕。
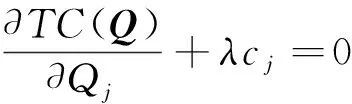
步骤1输入相关参数和计算精度ε;
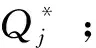
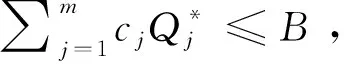
步骤4令λL=0,λU=λmax;
步骤5计算λ=(λL+λU)/2;
步骤6如果
(14)
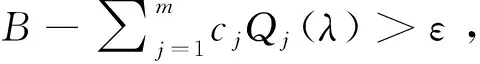
ε,转步骤7。
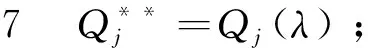
注意到Qj≥0,因此,若式(14)成立,则必有Qj=0成立。

图2 算法流程
5 数值实验
本节利用一个存在三种灾害事件的五种救援物资储备决策的算例来验证模型和算法的有效性。考虑存在三种可能的灾害事件,也即e={e1,e2,e3}。各种灾害事件发生的概率分别为β1=0.7、β2=0.2和β3=0.1。假设各灾害事件发生后的需求及对应的捐赠量均服从正态分布,参数如表1所示。
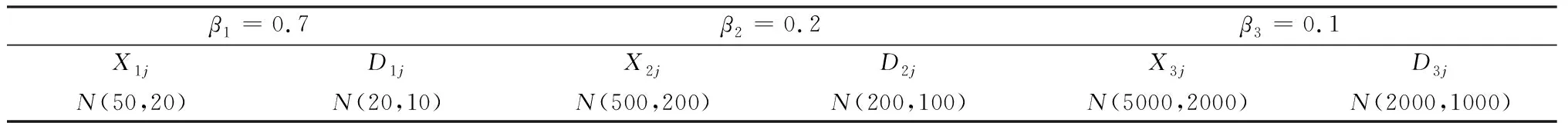
表1 需求与捐赠参数
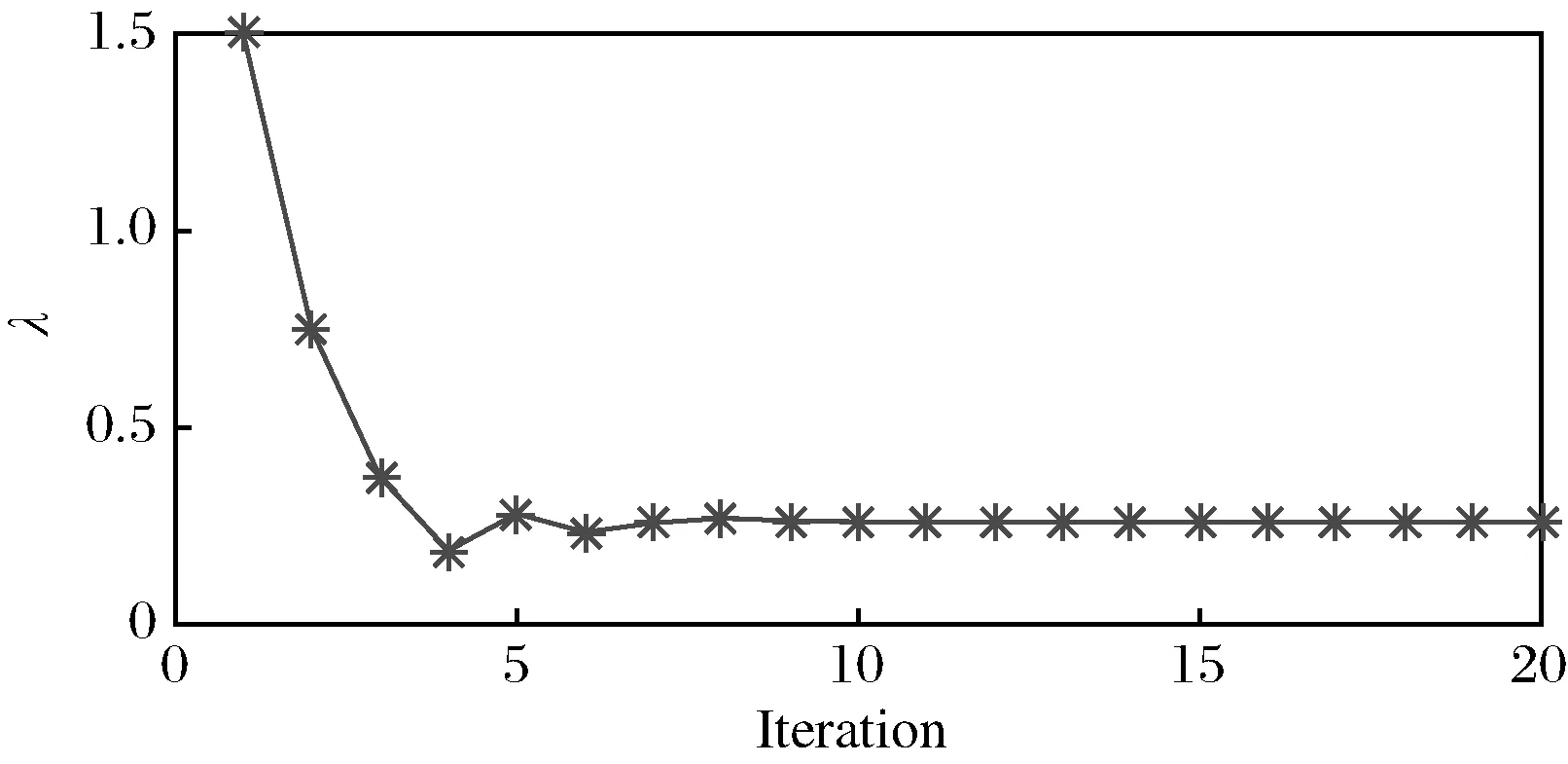
图3 迭代算子λ
各成本参数如表2所示,未列出的成本参数均设置为零。易知,参数设置是满足模型假设条件式(2)的。给定预算限制B=10000,表2给出了模型的最优解及其对应的最优期望成本。为了与无预算约束时的最优解及其成本进行比较,表2同时给出了有无预算约束的计算结果。本文的求解算法是在Matlab 8.5平台上开发的,计算精度设置为ε=0.001,方程求解使用的是Matlab库函数fzero,计算精度达到10-14。图3给出了本文算法迭代算子λ的收敛过程。
图3反映出本文设计的迭代求解算法收敛速度较快,在不到10步的计算后,迭代算子λ即收敛。

表2 计算结果
由表2的结果可知,本文设计的算法能给出任意精度所对应的模型最优解。另外,计算还反映出,预算约束使得NPO降低产品的储备量,而期望总成本因此而增大。为了进一步反映预算限制对于救援物资储备决策的影响,图4和5分别给出了不同预算限制对应的最优储备量和期望总成本的变化趋势。
给定B在区间[2000,18000]变化时,图4和5表明,当预算限制越来越紧时(B越来越小),最优储备量降低、期望总成本增大。当预算限制B由18000降至2000,期望总成本增大了4.08%,5个产品的最优订货量最低降至7.49%。由此可以发现,预算限制对于NPO的救援物资储备决策及其绩效产生了显著影响。另外,当预算限制B较小时,最优储备量增长的较慢,而期望总成本则下降的较快;当预算限制B较大时,最优储备量增长的较快,而期望成本则降低的相对较慢。当预算限制较紧时,一个相对较少的预算的增加,都会给整体救援效率的提高作出较大贡献。
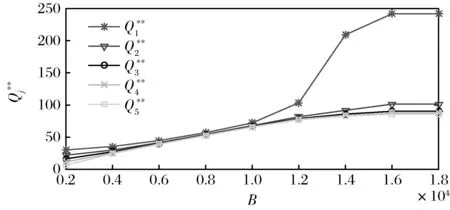
图4 最优储备量与B
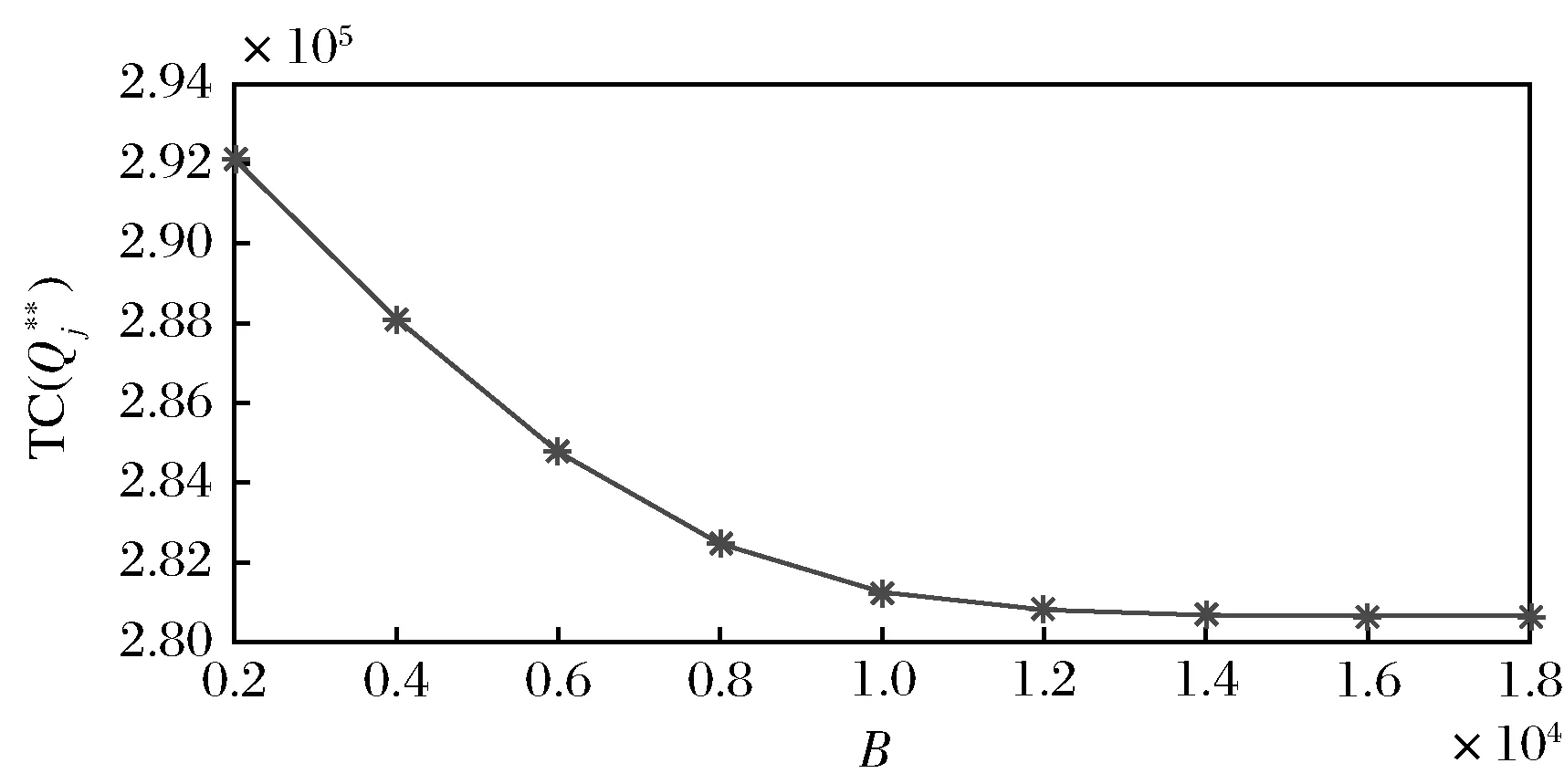
图5 最优期望总成本与B
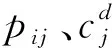
(1)当无预算约束时,若pij增大,则最优储备量增大;但这一结论并不适用于存在预算限制的储备决策。设定预算限制为B=10000时,pij增大可能会导致惩罚成本较低的产品的最优订货量减小。当然,无论有无预算约束,期望总成本会随着pij的增大而增大。

表3 参数和的灵敏度分析
6 结语
本文研究了多产品救援物资的储备决策问题。考虑多个可能的灾害事件的发生概率,进而联系各种灾害事件发生后的物资需求建立了救灾物资的组合随机需求模型,并在此基础上通过对现实救援物资交付的抽象提出了一种二阶段救援物资的交付过程模型,并建立了基于期望总成本最小化的救援物资储备模型,研究了模型的最优解。进一步考虑救援物资储备存在预算约束的限制,研究了具有预算约束限制的多产品救援物资储备决策模型,并利用二分法算法的思想开发了求解模型的算法。数值算例的计算结果表明,本文开发的算法能计算任意给定精度下的模型的数值最优解。另外,算法的迭代过程收敛速度也较快。
本文的研究结果可以服务于实际救援管理中的多产品救援物资储备决策,为制定合理有效的储备量决策提供借鉴与参考。另外,由于本文的模型是一种需求全部被满足的多产品Newsvendor问题,同时也考虑了使用捐赠物资和(或)现货市场购买物资的影响。因此,本文的研究结果对多产品Newsvendor模型及求解研究亦有贡献。但本文并未考虑多约束条件限制的模型求解,而实际救援储备工作中往往存在资金、仓库容量、救援时间等多个方面的约束,如何设计求解存在多个约束条件时储备决策模型是值得进一步开展研究的重要问题,特别是当这些约束均为紧约束时,设计有效的求解算法是极其重要的。另外,注意到本文模型中所提出的短缺物资的惩罚成本是难以测量的,这点与文献[16]和[17]中所提出的社会成本一样。因此,如何收集历史数据建立测度该成本的模型与方法也是值得进一步研究的问题。最后,本文并未考虑不同灾害事件对应的物资需求之间的相关性,这主要是因为相关性将会导致联合密度函数具有极其复杂的形式,使得期望成本函数的凸性难以保证。因此,未来的研究应加以考虑不同灾害事件之间需求的关联性。
