基于互信息的知识图谱实体关联关系建模与补全*
2018-07-13王珊蕾尹子都
夏 维,王珊蕾,尹子都,岳 昆
云南大学 信息学院,昆明 650500
1 引言
随着Linking Open Data等项目的全面展开,语义Web数据源的数量剧增,大量RDF(resource description framework)数据被发布,互联网正从仅包含网页和网页之间超链接的文档万维网(document Web)转变成包含大量描述各种实体和实体之间丰富关系的数据万维网(data Web)。在这一背景下,互联网公司逐步开始以此为基础构建知识图谱(knowledge graph,KG)[1-2]。KG为海量数据和领域知识提供了一种非常有效的组织方式,是一种结构化的语义知识库,如YAGO 的 YAGOKB[3]、DBpedia的 DBpediaKB[4]等。借助KG,人们可以从过去单一的网页链接转向实体链接;基于KG的搜索引擎,通过图结构反馈知识,帮助用户简单精确地实现知识的获取和定位,从而实现真正意义上的语义搜索。近年来,国际上主流的互联网公司或研究机构都加入到KG的研究中,研究人员在KG的构建[5]、表示学习[6-7]和补全(completion)[8-9]等方面开展了大量的研究。
KG是一种节点和边组成的图结构,其中节点表示相应的实体,边表示实体之间的关系。因为KG中节点之间的关联关系能够更好地完善搜索结果,服务用户,所以KG的完备性和准确性尤为重要。虽然当前知识库数量不断增多,规模不断扩大,但是仍然有许多知识库并不完整,例如Google Knowledge Vault[7]项目核心元素Freebase[10]中71%的个人信息缺失“出生地”,75%的个人信息缺失“国籍说明”,这使得KG的补全具有重要的实际意义。
针对图1中描述用户浏览商品相关信息的KG,补全就是判断和添加图1中虚线部分商品节点之间缺失的关系。

Fig.1 Knowledge graph of users'browsing on commodities图1 用户浏览商品KG
针对KG补全,目前国内外学者开展了许多系统性的研究。例如,Liu等人[2]综述了KG中通过实体间关系抽取来补全KG的相关概念和研究领域,介绍了关系抽取的经典模型,大多数KG补全的方法都是以表示学习和知识推理为基础。其中,从表示学习方面,Zhang等人[11]提出一种实体间相似性度量标准,以及利用实体间常见语义模式来估计三元组间是否存在关系的方法;Minervini等人[12]提出一种统一的方法,利用潜在因素模型(latent factor model)中包括实体类别与子类关系的附加模式知识,实现KG中缺失链接的预测。这些方法仅仅以已有的KG中的知识为基础进行关系抽取,忽略了KG中错误的链接,从而导致实体间关系预测错误。从知识推理方面,Lao等人[13]提出一种基于路径的知识推理方法,将每种不同的关系路径作为一维特征,通过统计KG中大量的关系路径来构建关系分类的特征向量,建立关系分类器进行关系抽取;Gardner等人[14]在大规模语料库上标记潜在特征的边,旨在提升基于路径排名算法KG补全准确率。但是,KG中比较稀疏且连通性较差的实体关系不利于关系的抽取,很难有效地补全KG中节点间的缺失关系。
事实上,随着社交网络的普及和广泛应用,用户行为记录依托多种媒介快速产生,即使对于同一实体集,用户行为中体现出来的实体间的关联关系,仍有可能与KG中的描述并不相同。也就是说,KG和用户行为记录,分别从领域知识库和用户生成数据(user-generated data,UGD)这两方面描述了实体间的关联关系。从用户行为记录产生和KG构建的角度看,急剧增长的数据中所蕴含的知识,也是KG所描述领域知识的有益补充。分析UGD中实体间的关联关系,既可以修正KG中单一的实体间错误的关联关系,又可克服KG中因为节点间关系稀疏性和连通性差而使得所抽取关系不准确的问题。因此,在UGD中找出实体节点间的关联关系,对KG进行补全,在一定程度上可保证实体间关联关系的可靠性和完整性。为了有效实现KG补全,本文需要解决如下问题:
(1)如何从UGD中发现实体间存在的关联关系。
(2)如何有效、准确地利用UGD中实体间的关联关系来完成KG补全。
互信息被广泛应用于文本信息处理等领域[15],常用于描述两个变量之间的关联程度。UGD中实体之间的关系具有不确定性和依赖性,相比关联规则等度量方法,互信息更能表示不确定信息之间的依赖关系。本文以互信息作为计算UGD中实体间关联关系的基础,从而根据“实体—关联度—实体”三元组的形式构建实体关联图(entity association graph,EAG)。针对海量的UGD,传统的集中式计算平台难以处理海量数据,Spark分布式计算架构是高效处理海量数据的典型代表[16],其中的GraphX框架为EAG中海量节点的图结构操作提供了有效的支持。本文以Spark作为计算框架,在Spark之上实现EAG的构建和KG补全的算法。
在EAG结构中,相邻实体节点间一般具有共同的属性,因此可以从实体节点的相邻实体节点出发,来判断实体间是否存在潜在的关联关系。例如,通过实体节点“鼠标”分别与“键盘”和“电脑”之间的关联,来判断“键盘”和“电脑”之间是否存在潜在关联关系。本文将一个实体节点与相邻实体节点之间的关联关系看作为一种影响(influence),一个实体节点与两个互不相邻的实体节点均相邻,则将一个实体节点对这两个互不相邻的实体节点的影响综合起来表示这两个实体节点之间的关联影响。文献[17]给出了一种计算多个因素联合影响的方法,本文基于此给出一种关联影响叠加(superposition)的方法,从而计算实体节点之间的关联影响值。两个实体节点之间可能存在多个与这两个实体节点均相邻的实体节点,因此可能存在多个关联影响值。为了有效估计实体节点间的关联度,本文将多个关联影响值再次叠加,从而得到这两个实体节点之间的综合关联值,进而判断这两个实体节点之间是否存在潜在关联关系。在淘宝网真实数据[18]上进行了实验,验证了本文方法的高效性和有效性。
2 基于互信息的实体节点关联模型构建
在电子商务背景下,UGD是用户浏览网页或者购买商品等行为产生的记录,将网页或者商品作为实体,一条行为记录表示一个用户对某种实体的行为。用U={u1,u2,…,um}表示用户集合,O={o1,o2,…,om}表示实体节点集合,B={1,2,…,h}表示用户行为集合,集合B中的元素代表“浏览”、“购买”或“收藏”等行为,一条用户行为记录表示为{u,o,b},其中u∈U,o∈O,b∈B。表1给出了一个UGD片段。

Table 1 Fragment of UGD表1 UGD片段
下面给出KG的定义,作为后续讨论的基础。
定义1(KG)用GK=(VK,EK)表示KG,其中VK={v1,v2,…,vy}为实体节点的集合,EK={e1,e2,…,el}(l≥1)为实体之间边的集合。任意一条边el=(vi,vj),vi,vj∈EK,i≠j且1≤i,j≤r,节点vi称为始点,节点vj称为终点,节点vi和vj之间的关系由标签(label)表示。
UGD中实体节点间的关系可以作为KG中实体节点间缺失关系的有益补充,下面给出实体节点关联模型的定义,用以表示UGD中实体节点集合中不同实体之间的关联关系。
定义2(实体节点关联模型)M=(O,I,ε)称为UGD中实体节点关联模型,其中O={o1,o2,…,on}表示UGD中实体节点的集合,且O≠VK,O⋂VK≠∅,I表示实体节点之间的关联值,其中0≤I≤1,ε表示给定的关联阈值,0≤ε≤1。
2.1 基于互信息的实体节点关联关系度量
互信息[19]的定义如式(1),是实体间关联关系度量的基础。

定义3(互信息)对于O中任意的两个实体节点op和oq(p≠q),0≤p,q≤n,它们之间的关联值定义为:
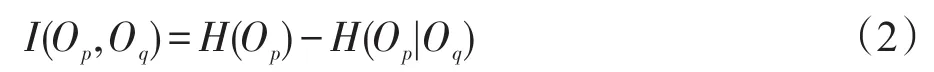
为了方便计算,对式(2)做如下等价变化:
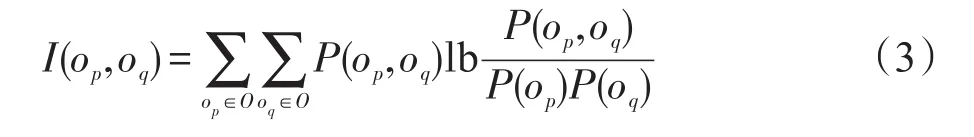
其中,0≤I(op,oq)≤ 1;P(op,oq)表示O中op和oq的联合概率;P(op)和P(oq)分别表示O中op和oq的概率。

其中,N(op,oq)表示在用户行为记录中出现实体节点op或oq的用户行为记录条数;N(op)表示出现op的条数;N总表示总的用户行为记录条数。以表1中的UGD片段为例,(o1,o2)同时出现的次数为1,o1和o3同时出现的次数为0,o2和o3同时出现的次数为1,因此N(o1,o2)=3,P(o1,o2)=0.75。可见,两个实体节点op和oq同时出现的概率越大,I(op,oq)越大,op和oq之间的关联关系就越强。给定阈值ε,若节点之间关联度不小于ε,则节点之间的边真实存在。
2.2 EAG的构建
基于前述方法,可以得到实体节点之间的关联关系,下面给出EAG的定义。
定义4(EAG)用G=(O,A)表示实体节点关联图(EAG),其中O={o1,o2,…,on}为实体节点集合,A={a1,a2,…,as}表示EAG中边的集合。若O中任意两个实体节点ox和oy(1≤x,y≤n,x≠y)有边相连,则表示ox和oy之间存在关联关系。
EAG中相互关联的实体节点之间存在相互影响,一个实体节点的出现必然会影响另一个实体节点的出现,另一个节点的出现也会影响该节点的出现,但影响的程度往往并不相同,因此实体节点关联关系具有方向性。例如,顾客购买电脑的同时可能也会购买键盘。借鉴文献[20]中的判断方法,采用式(6)来判定关联的方向,其中e(ox→oy)表示关联关系方向由实体节点ox指向实体节点oy,e(ox←oy)表示关联方向由实体节点oy指向实体节点ox。假设ox的出现次数表示为|Mx|,oy的出现次数表示为|My|,ox和oy出现的次数用集合表示为|Mx⋂My|,则有:
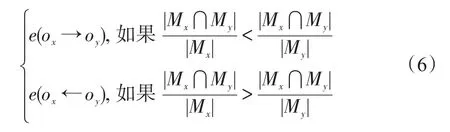
针对UGD中大量的实体节点,以Spark作为编程模型,使用式(3)来衡量两个实体节点之间的关联程度。首先统计UGD中每个实体节点出现的次数,以<key,value>对形式表示,其中key表示实体节点,value表示实体节点出现的次数;然后对每个实体节点进行Map操作,统计实体节点中每对实体节点的出现次数。
算法1实体节点关联模型

算法1中,构建EAG模型的时间开销主要取决于任意两个实体节点之间的组合。若EAG中有n个实体节点,步骤4、步骤5的执行时间远小于O(n2),步骤7、步骤8和步骤9的执行时间为O(n2),因此算法1的时间复杂度为O(n2)。针对实际中规模较大的UGD,下文进一步通过实验来测试算法的有效性。
例1以用户浏览商品为例,若UGD中包含1 000条用户行为记录,由算法1的步骤5得到N(“鼠标”)=325,N(“键盘”)=400,由步骤6得到 N(“鼠标”,“键盘”)=187 ,则根据上述式(2)、(3)、(4)、(5)、(6)得到0.71>0.58,因此“鼠标”和“键盘”之间边的方向为“鼠标”➝“键盘”。同理可计算出其他实体节点间的关联度以及它们之间边的方向,如图2所示。
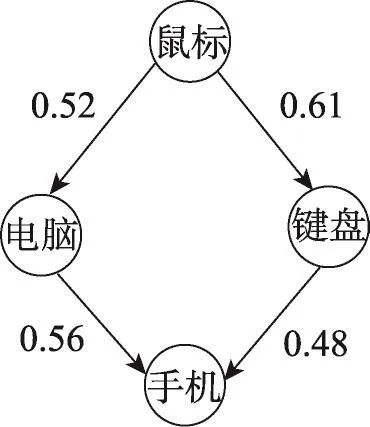
Fig.2 EAG of commodities图2 商品EAG
3 KG的补全
若GK中实体节点间缺失的边在G中真实存在,则把这条边添加到GK中;若GK中实体节点间缺失的边在G中不存在,则把这样的节点之间的关联称为潜在关联,进而通过判断潜在关联的强弱来确定这两个节点之间是否需要添加边。
3.1 实体节点间潜在的关联关系度量
G中一个实体节点op均与两个不相邻的实体节点oq和oz相邻,且它们之间的关联值分别记为I(op,oq)和I(op,oz)。在实际情形中,一个实体节点与两个不相邻的实体节点之间关联值越高,且关联值越接近,则这两个不相邻的实体节点之间的潜在关联关系越高,反之,则越低。本文综合考虑一个实体节点对两个不相邻的实体节点之间产生的关联影响,引入“叠加”的概念[18]。将该实体节点对两个不相邻的实体节点之间的影响而产生的关联影响值记为I(op,oq)⊕I(op,oz),且叠加算子⊕应满足:
(1)有界性,0≤ I(op,oq)⊕I(op,oz)≤ 1,这保证了多个关联值可以通过两两叠加来实现。
(2)交换律,I(op,oq)⊕I(op,oz)=I(op,oz)⊕I(op,oq),这保证了一个实体节点对两个不相邻的实体节点之间的潜在关联的影响是一个不变的值。
基于上述思路,下面给出不相邻实体节点之间潜在关联关系的定义。
定义5(关联影响)在O中存在任意3个实体节点 ob、oc和 od,ob分别与 oc和 od相邻,oc与 od不相邻,其中ob和oc之间的关联度为I(ob,oc),ob和od之间的关联度为 I(ob,od),且有 ε≤ I(ob,oc),I(ob,od)≤ 1,0≤b,c,d≤ n,b≠ c,b≠ d且 c≠ d,则 oc和 od之间的潜在关联关系受实体节点ob的影响而产生的关联影响为:
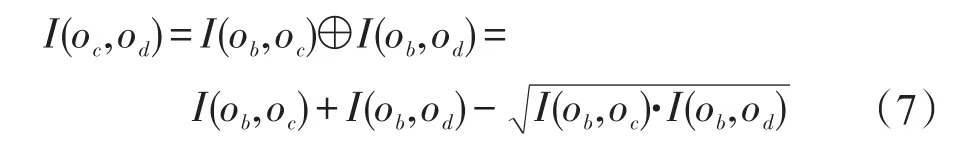
可见,如果式(7)中I(ob,oc)和I(ob,od)越大且越接近,则I(oc,od)就越大,反之则越小。
3.2 关联影响值的叠加
G中的实体节点数多,且结构复杂,但是可能存在多个实体节点与两个不相邻的实体节点均相邻,因此这两个不相邻的实体节点可能有多个关联影响值。基于上述思想,针对两实体节点间存在多个关联影响值的情况,下面给出对多个关联影响值进行叠加的方法,从而得到不相邻实体节点间的综合关联值,定义如下。
定义6(综合关联值度量函数)不相邻实体节点oc和od之间有多个关联影响值I1(oc,od),I2(oc,od),…,Iz(oc,od),其中z为oc和od共同的邻居实体节点的个数,则oc和od的综合关联值度量函数 f定义如下:
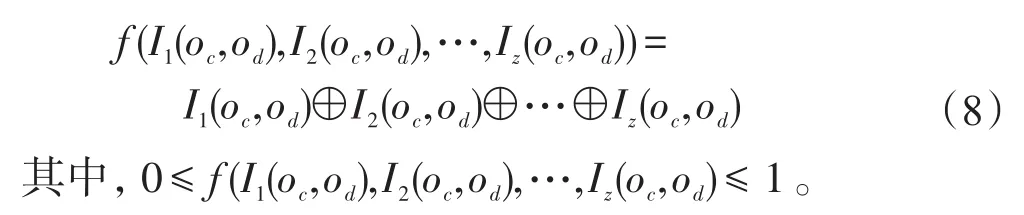
若 f(I1(oc,od),I2(oc,od),…,Iz(oc,od))≥ ε(0≤ ε≤ 1),则认为这两个实体节点间存在强的潜在关联,需要在这两个实体节点之间添加一条边。
GK中实体节点间缺失的边,如果在G中存在,则将该边补全到GK中,本文统一给商品和商品之间添加“influence”的标签,进而实现KG中实体节点间缺失关系的补全。上述思想见算法2。
算法2KG补全


算法2中,若UGD中包含n个实体节点,步骤4、步骤5的执行时间为O(n2),步骤10的执行次数远小于O(n2),而算法2的主要时间开销是寻找相邻实体节点的三元组,即为步骤4和步骤5,因此算法2执行时间为O(n2)。针对大规模KG,算法2的实际执行性能将通过实验进一步测试。
例2图2中不相邻的实体节点“电脑”和“键盘”间存在“鼠标”和“手机”,且“鼠标”和“手机”都与“电脑”和“键盘”相邻,根据式(7)可计算出“电脑”和“键盘”之间的关联受“鼠标”的影响,且产生的关联影响值为0.56。同理,基于“手机”对相邻的“电脑”和“键盘”之间关联关系的影响,其间的关联影响值为0.52。再由式(8)得到“电脑”和“键盘”的综合关联值为0.54。若δ=0.52,由于0.54>0.52,因此在实体节点“电脑”和“键盘”之间添加一条边。
4 实验结果
为了测试本文提出方法的有效性,采用淘宝网真实用户行为记录作为实验数据集[17],包含2 000个用户、350 889件商品和1 048 576条用户行为记录,格式为user_id::item_id::behavior_ty。实验环境如下:1台主频为3.3 GHz的4核CPU、内存16 GB的计算机作为Master节点,9台主频为3.3 GHz的8核CPU、内存16 GB的计算机作为Worker节点,构建了Spark分布式计算平台。本文测试了构建EAG的效率、加速比和并行效率以及KG补全的有效性。
4.1 EAG的构建效率
为了测试构建EAG的效率,本文随机选取了淘宝数据集中的2.5×105、5.0×105、7.5×105和10.0×105条用户行为记录数据,并分别测试了Worker数量为3、6和9情形下算法1的执行时间和加速比。由图3可见,随着数据规模的增大,不同Worker数量下的执行时间均增大。
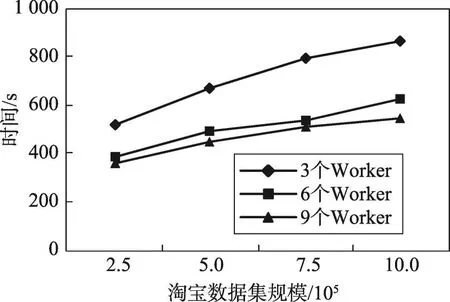
Fig.3 Time of EAG construction图3 构建EAG的时间
并行算法的加速比是单个节点情况下执行时间与多节点情形下执行时间的比值。图4给出了随着数据规模增大,不同Worker数量情形下算法1的加速比。图5给出了随着Worker数量增加,不同数据规模情形下算法1的加速比。可以看出,随着数据规模的增大,Worker数量越多,加速比增加越快。但在数据为5.0×105和7.5×105情形下,6个Worker和9个Worker时的加速比增加明显,因为在随机选取的5.0×105和7.5×105条用户行为记录中,商品节点数量趋近于商品总数,多个Worker处理商品节点的优势较显著。
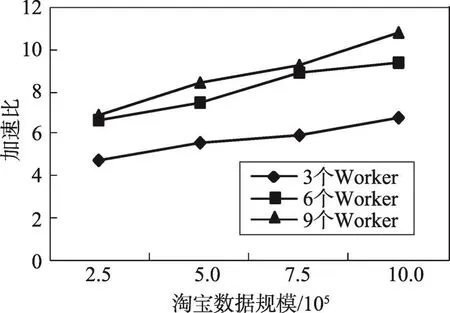
Fig.4 Speedup ratio ofAlgorithm 1 with various scales of data sets图4 不同数据集规模情形下算法1的加速比
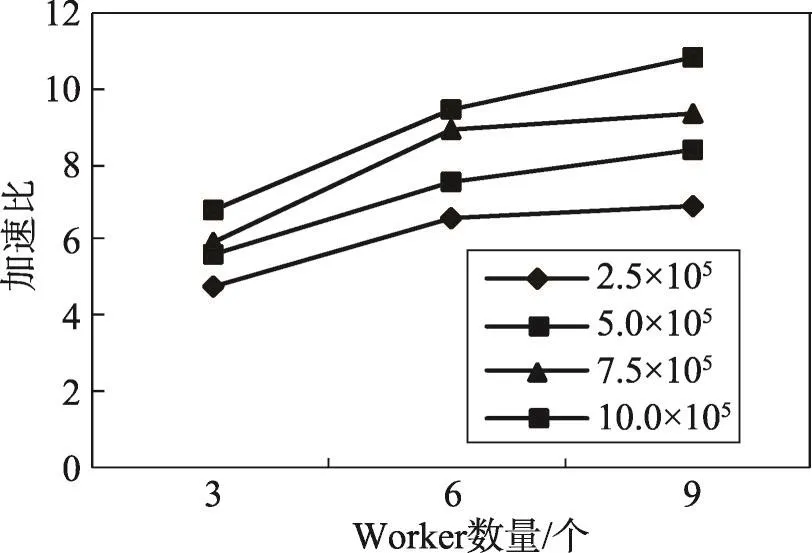
Fig.5 Speedup ratio ofAlgorithm 1 with various numbers of Workers图5 不同Worker数量情形下算法1加速比

Fig.6 Parallel efficiency ofAlgorithm 1 with various numbers of Workers图6 不同Worker数量情形下算法1并行效率
并行算法的并行效率是加速比与节点数的比值,图6给出了随着Worker数量增加,不同数据规模算法1的并行效率。可以看出,随着Worker数量的增加,不同数据规模的并行效率都降低。图7给出了随着数据规模的增加,不同Worker数量情形下的并行效率。可以看出,随着数据规模的增加,不同Worker数量的并行效率都增加,且同一Worker数量时,数据规模越大,并行效率越高。这说明算法1对于大规模数据具有良好的可扩展性。

Fig.7 Parallel efficiency ofAlgorithm 1 with various scales of data sets图7 不同数据集规模情形下算法1并行效率
4.2 KG补全的有效性
为了测试本文从UGD中得到的实体节点之间的关系补全KG的有效性,首先假设UGD中实体节点间的关联关系是真实、正确的,并以之作为补全KG的基础。为了保证实体节点间的关联具有一定的可靠性,从数据集中随机选取该数据集的5%比例的具有相关联的实体节点,并取它们的关联值的平均值作为阈值δ。考虑到不同数据集下的δ值可能不同,分别从20%,30%,…,80%的数据集比例下计算δ值,再从不同比例数据集构建的EAG中,随机选取5%比例的边,根据与选出的5%比例的边的相邻节点来计算它们的综合关联值,并与真实的关联值对比来证明算法2的有效性。若真实的关联值与算法2中得到的综合关联值同时小于或者同时大于阈值δ,即算法2得到的实体节点间关联性与真实的关联性一致,则表示算法2正确。如表2所示,算法2的正确率为70.02%,这从一定程度上说明了算法2的有效性。
此外,从另一个角度来测试本文基于互信息的补全方法的有效性。将数据集分为训练集和测试集两部分,并将数据集中得到的实体节点在不同比例的训练集中测试本文方法(MI)的准确性。由于本文所提出的补全KG的方法是一种基于图上的实体节点间关联关系的叠加推理,Path Ranking方法(PRA-paths)[21]是通过连接实体的已有路径来预测实体间的潜在关系,从而补全KG,这两种方法都是通过已有的路径进行知识推理来补全KG,具有一定的可比性。因此选取PRA-paths方法与MI方法进行对比来证明MI方法的有效性。在本实验中,选择准确率(Precision)、召回率(Recall)和F值作为衡量KG补全算法的指标,分别如式(9)和(10)所示:

Table 2 Accuracy ofAlgorithm 2表2 算法2的正确率

其中,Pre表示准确率;F0表示补全的边也是测试边;N(F0)表示补全的边也是测试边的条数;F表示补全的边;N(F)表示补全的边的条数;Rec表示召回率;T表示测试边;N(T)表示测试边的条数。
F值综合衡量了准确率和召回率,公式如下:

实验中,分别从淘宝数据集中随机选取出20%、30%、40%、50%、60%、70%、80%作为训练集,根据不同比例的训练集得到的结果如下,从图8和图9可以看出,随着训练集比例的增加,MI方法和PRA-paths方法的准确率均先增加再降低,召回率逐渐增加。因为随着训练集比例的增加,实体节点增多,图的连通性好,使得KG补全的准确率和召回率提高。当训练集比例多于50%时,实体节点增加速度降低,图的连通性趋于最大,得到的补全的边不断增多,召回率不断提高,同时得到的无关的边也在不断增多,使得KG补全的准确率降低。当训练集低于50%时,MI方法准确率高于PRA-paths方法,原因在于训练集比较小的时候,实体节点较少,图的连通性较差,MI方法在图的低连通性下比PRA-paths方法的准确率高。本文还测试了不同比例的训练集下的F值,从整体上衡量算法的有效性。由图10可以看出,MI方法的F值在训练集比例小于65%时均高于PRA-paths方法,因为在连通性低的图中不利于PRA-paths方法的推理。在训练集高于65%时,虽然MI方法的F值低于PRA-paths方法,因为MI方法在连通性较好的图中得到无关的边比PRA-paths方法多,但是两种方法F值的差距并不大且MI方法的F值略大于PRA-paths方法的F值,所以与PRA-paths方法相比本文提出的MI方法较为理想。
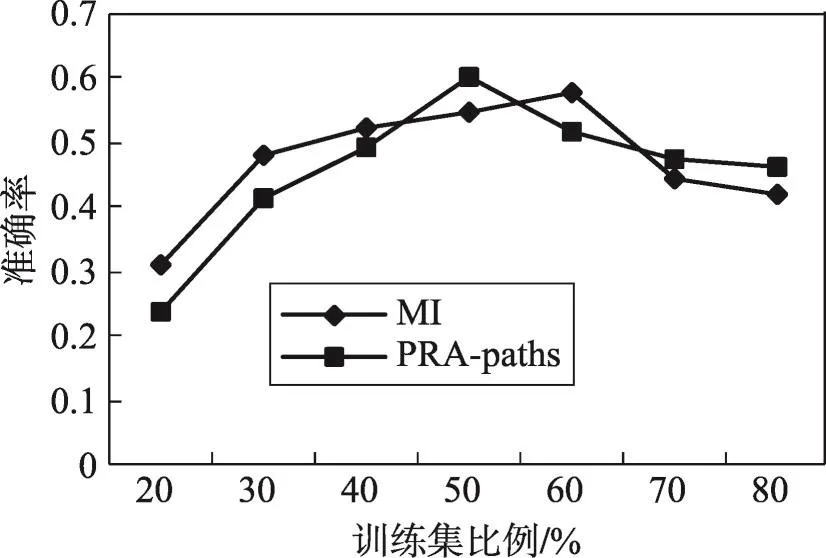
Fig.8 Precision图8 准确率
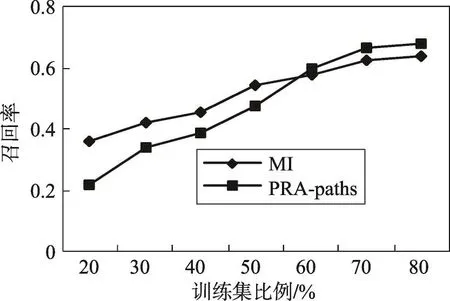
Fig.9 Recall图9 召回率
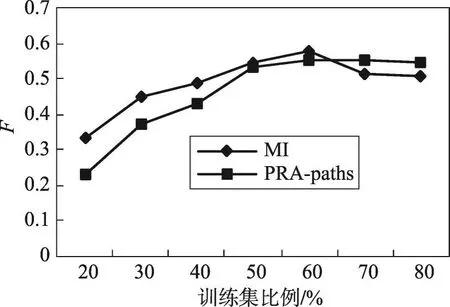
Fig.10 F scores图10 F值
5 总结与展望
本文针对KG中实体节点间缺失的关系,结合UGD,通过互信息计算实体节点之间的关联关系,进而构建EAG,并根据EAG的结构,提出一种叠加的方法来计算不相邻实体节点间的潜在关联关系,从而补全KG。本文用UGD中的实体节点之间的关联关系来补全KG,解决了KG中因为实体节点间关系稀疏而导致关系抽取不准确的问题。但是当UGD的规模较大时,得到的EAG图结构比较复杂,准确率较低且代价较高,因此未来的工作将考虑在实体间添加标记,去掉那些关联关系较“弱”的实体节点,从而提高KG补全的准确率。
