分布式随机方差消减梯度下降算法topkSVRG*
2018-07-13王建飞亢良伊
王建飞,亢良伊,刘 杰,叶 丹
1.中国科学院 软件研究所 软件工程技术研发中心,北京 100190
2.中国科学院大学,北京 100190
1 介绍
在机器学习领域,机器学习问题通常转换成一个目标函数,然后利用优化算法求解目标函数中的参数,因此优化算法在机器学习中具有非常重要的地位。
给定n个训练样本,xi表示输入向量,yi为输出,(x1,y1),(x2,y2),…,(xn,yn),xi∈Rd,yi∈R ,求解一个目标函数确保每个样本对应输出与已知输出误差最小。利用φ表示目标函数,目标函数表示为:

通常利用标准的梯度下降(gradient descent,GD)进行求解,更新公式如式(2)所示:
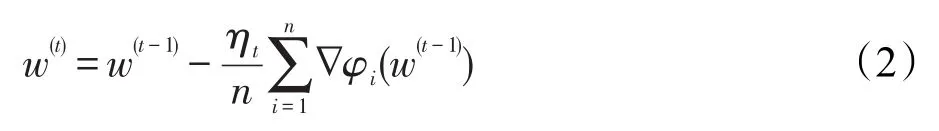
然而,每一步模型更新,需要计算所有样本点的梯度,代价较大。一个更加高效的算法是随机梯度下降(stochastic gradient descent,SGD)[1],每次随机从数据集中选择一个样本点it进行梯度更新,即式(3):

随后,针对类似的大规模分布式机器学习问题,SGD出现了改进的Mini-Batch[2]版本。随机选取m个样本进行并行或者分布式计算,(x1,y1),(x2,y2),…,(xm,ym),xi∈Rd,yi∈R ,其中 m 代表批(batch)的大小,然后使用式(4)更新模型:

理论分析和实践经验表明,SGD是大规模机器学习问题比较好的求解方法,具有广泛应用。然而SGD在稳定性方面还有所欠缺,容易受噪声梯度的影响,在固定学习率的情况下,很难达到某一最优解,在学习率逐渐减小的情况下,只能达到次线性的收敛速率。
针对SGD受噪声干扰的问题,文献[3]提出了随机方差消减梯度算法(stochastic variance reduction gradient,SVRG),核心思想是利用全局的梯度信息对每次用于模型更新的梯度进行修正。理论分析可以证明SVRG具有线性收敛速率。因为SVRG是单机串行算法,难以应用到大数据环境。已有的分布式SVRG算法(distributed SVRG,DSVRG)[4]采用循环节点更新策略,并不是完全的并行化,SCOPE(scalable composite optimization for learning)[5]理论证明了线性收敛性,但是存在较难调优的参数。因此,本文对原始SVRG的模型更新进行了改进,提出一种新的算法topkSVRG(top-k model average based SVRG)。其改进在于:主节点维护一个全局模型,从节点基于本地数据进行局部模型更新,每轮迭代时,选择与当前全局模型距离最小的k个局部模型进行平均来更新全局模型,参数k调大可以提高收敛速度,调小k可以保证收敛。topkSVRG的动机也是通过选择与全局模型最近的局部模型,来减少噪音的影响。本文理论分析了算法的线性收敛性,基于Spark进行算法实现,通过与Mini-Batch SGD、CoCoA、Splash及相关算法的实验比较,topkSVRG可以在高精度要求下更快地收敛。topkSVRG鲁棒性比较好,在稀疏数据集、稠密数据集上都可以取得不错的加速效果。
本文主要贡献有如下两点:
(1)提出了一种新的分布式SVRG实现算法,通过k个最近似局部模型来更新全局模型,从而加快收敛速度,并进行了基本的理论分析。
(2)基于Spark平台进行了算法的分布式实现,与Mini-Batch SGD、CoCoA、Splash,以及Mini-Batch SGD结合Adadelta、Adagrad、Adam和Momentum等算法进行了评测对比,证明了topkSVRG在高精度要求下收敛速度较快,这与原始SVRG的实验效果一致。
本文组织结构如下:第2章介绍了主流的分布式梯度下降算法;第3章提出了topkSVRG算法,并且理论分析了该算法的线性收敛性;第4章给出了实验评测方案和结果;第5章进行了总结和展望。
2 相关工作
梯度下降法是应用最广泛的优化方法,有大量相关工作,本文主要介绍三类:(1)以Mini-Batch SGD为基础的相关优化;(2)分布式SVRG的相关工作;(3)其他分布式SGD的重要工作。本文面向凸优化问题,因此不介绍深度学习相关优化算法。
分布式环境下目前主流的方法都是基于Mini-Batch的思想,Spark目前实现了Mini-Batch SGD算法,用于支持MLLib[2]大量模型求解,但是该算法存在收敛速度慢,稳定性欠缺,难以确定学习率等问题[6]。于是出现了自适应学习率的Momentum[7]、Adagrad[8]、Adadelta[9]、Adam[10]等优化方法,这些方法不改变Mini-Batch SGD的执行逻辑,比较容易进行分布式实现。
随机方差削减梯度(SVRG)[3]是噪声梯度去除方法中的典型方法。这个方法的整体思路是:为了提高梯度计算的准确性,利用全局的梯度信息对每次用于模型更新的梯度进行修正。理论分析和实践经验表明,串行SVRG可以取得目前几乎最好的单机收敛速度。随后,诸多学者研究分布式模式下的SVRG方法。Jason等人提出了DSVRG[4],证明了在数据随机划分的条件下,相比其他一阶优化方法,可以取得最优的运行时间、最少的通信次数等。但是DSVRG存在如下问题:该算法是单机多线程模式,每个线程代表一个计算节点,通过节点之间相互传递消息,实现参数的更新。本质上来讲,这种循环更新模式是串行的,当一个机器更新模型的时候,其他机器会存在等待的情况,不是真正意义上的分布式并行。针对该问题,Zhao等人提出了SCOPE[5],其是对SVRG的分布式实现,理论证明了该方法具有线性的收敛速度,并且通过实验表明,在很多数据集上SCOPE可以取得明显优于其他分布式SGD的收敛速率。但是在SCOPE中,收敛保证因子C难以确定(C的取值范围太大),如果设置太小,会降低收敛速率,如果设置太大,可能导致不收敛。
Jaggi等人提出了CoCoA[11],CoCoA是一种分布式坐标下降方法,该方法在梯度计算过程中会对模型进行本地更新,从而使得最后每个计算节点计算出的模型更加准确,然后进行全局的聚合操作,有效地减少了全局的通信次数。Zhang等人提出了Splash[12]。Splash的核心思想是:首先将集群中的计算单元分成K组,然后每个计算处理单元使用本地数据计算本地模型,K个组分别合并组内的模型,通过交叉验证法选择K组内最好的模型,从而获得更为精准的计算结果。
3 topkSVRG算法
本章首先简单介绍SVRG原始算法,然后介绍本文提出的topkSVRG算法。
3.1 串行SVRG
为了降低梯度噪声,SVRG通过全局的梯度进行修正。SVRG中,每个计算节点使用式(5)、(6)进行更新:


其中,w∈Rd表示模型参数;η表示更新步长;∇Rn(wt)是使用上一轮的模型wt计算出的平均梯度;∇fij(wt)表示函数 f在样本点ij的梯度;∇fij(wt)-∇Rn(wt)是梯度的偏差是经过修正的梯度,是无偏的,使用更新模型算法伪代码如算法1所示。
算法1SVRG(T,m,η)

从wt到wt+1需要2m+n次梯度计算,其中步骤3执行n次,步骤7执行2m次。因此,每轮迭代需要2m+n次梯度计算,SVRG的单次迭代代价比SGD(m次梯度计算)要大。实践经验表明:在大多数应用上,SVRG比SGD收敛速度更快,其具有线性收敛率[3],尤其是需要大量数据集遍历(epochs)的时候。此外,算法1步骤1对w1进行初始化,对于凸优化问题,可以通过运行1轮SGD确定;对于非凸优化问题,可以运行大约10轮SGD确定。
3.2 分布式SVRG
分布式实现SVRG的主要目的是每轮迭代,由多个节点通过Mini-Batch的方式来计算梯度,更新局部模型。主要难点在于主节点每轮更新模型的时候如何在有效利用每个计算节点计算结果的同时,又能保证算法的收敛性。如果直接对从节点模型进行平均可能导致不收敛;SCOPE[5]通过增加一个收敛保证因子来确定收敛性,但是参数较难确定。本文提出一种直观的方法,主节点维护一个全局模型,从节点基于本地数据进行局部模型更新,每轮迭代时,选择与当前全局模型距离最小的k个局部模型进行平均来更新全局模型,参数k调大可以提高收敛速度,调小k可以保证收敛。该算法的动机也是通过选择与全局模型最近的局部模型,来减少噪音的影响。因此算法命名为topkSVRG。topkSVRG架构如图1。
算法伪代码如算法2所示。topkSVRG主要包括4阶段:
(1)计算平均梯度,采用Spark实现分布式计算,如步骤3所示;
(2)多个计算节点并行地按照串行SVRG的模型更新策略更新模型,如步骤4~步骤11所示;

Fig.1 Framework of topkSVRG图1 topkSVRG架构图
(4)平均这k个模型,从而获得最终的模型wt+1,如步骤16所示。
算法2分布式SVRG(T,K,k,h,r,η)

3.3 算法实现
本文提出的topkSVRG基于整体同步并行计算模型(bulk synchronization parallel computing model,BSP)[13],适合目前主流的Spark平台。通过Spark RDD[14](resilient distributed datasets)操作,可以方便高效地实现上面的每一个过程,具体说明如下:
(1)通过Spark RDD的map、aggregate操作实现平均梯度的计算。
(2)通过Spark RDD的mapPartition操作实现各个计算节点的并行计算。
(3)主节点通过Spark RDD的takeOrdered操作获取k个与上一轮模型最接近的模型。
(4)主节点通过Spark RDD的average操作对k个模型进行平均。
具体实现参见实验部分所示地址http://github.com/codlife/Ssgd。
3.4 算法收敛性分析
本文提出一种“top k最邻近模型平均策略”,即主节点聚合每个计算节点模型的时候,选取k个与当前模型最接近的模型,对这k个模型进行平均。该策略是算法收敛性证明的关键。算法收敛性分析如下:单机串行SVRG每一轮迭代有式(7)成立。其中L为常数,w*是模型的最优解,因此串行SVRG具有线性收敛速度[6]。

本文提出的topkSVRG中每个计算节点同样有式(8)成立。其中 p表示第p个计算节点,K表示节点个数。

假设各个wpt都比较接近,通过平行四边形法则可以证明,对于任意两个 wpt、wit、wjt有式(9)、(10)成立:

由式(8)可以得到式(11)成立:

由式(9)、(10)、(11)可以得到式(12)成立:

式(12)表明:当每个计算节点的计算结果wpt比较接近的时候,直接对模型进行平均可以获得和单机串行SVRG相同的线性收敛速率。
关于参数k,在初始数据随机划分的情况下,将k设置为计算节点的个数能够取得较快的收敛速度;通过缩小k,可以保证收敛。通常建议将k设置为Round(0.9×K)、Round(0.8×K)、Round(0.6×K)、Round(0.5×K)(Round为下取整操作)等几个常见的值。
4 实验评测
针对求解L2正则化的逻辑回归(logistic regression,LR)[15]的场景,对本文提出的方法和一些实验基准(Baseline)进行评测。目标函数如下所示:


Table 1 Dataset表1 数据集
其中,学习率η设置为(t是迭代轮数);采样因子r设置为0.1;计算节点内循环次数h设置为1 000。
对于参数设置:本文的实验超参数λ设置为10-4;参数k,实验1、实验3数据集都是稀疏数据集,k设置为Round(0.8×K),实验2数据集是稠密数据集,k设置为Round(0.9×K),实验4测试数据集较多,k设置为Round(0.8×K),以获得一个比较稳定的收敛过程。
4.1 数据集
本文使用多个数据集进行测评,从LibSVM网站获取,选取具有代表性的数据集,实验数据集如表1所示。
4.2 实验环境和实验基准
使用具有10个节点的Spark集群,Spark采用2.0版本。集群配置如表2所示。

Table 2 Machine configuration表2 机器配置
实现了本文提出的topkSVRG和工业界广泛使用的Mini-Batch SGD、Mini-Batch SGD with Adadelta、Adagrad、Adam、Momentum。同时将上述算法和CoCoA、Splash等算法进行对比。
4.3 实验结果
实验结果如图2~图4所示,图中的纵轴为对模型精度取对数lg。
实验1基于Rcv1数据集(高维,稀疏,N>>d),实验结果如图2。通过该实验可以发现,在高维稀疏样本数远远大于特征维数的数据集上有以下特点:

Fig.2 Experiment on Rcv1 dataset图2 数据集Rcv1上的实验
(1)topkSVRG收敛速率相比其他分布式SGD加速明显,并且可以达到较高的收敛精度。这是由于在稀疏数据集上,其他分布式SGD更易受梯度噪声的影响。
(2)Spark Mini-Batch SGD稳定性欠缺。
实验2基于Susy数据集(低维,稠密,N>>d),实验结果如图3。通过该实验可以发现,在低维稠密样本数远远多于特征维数的数据集上有以下特点:

Fig.3 Experiment on Susy dataset图3 数据集Susy上的实验

Table 3 AUC on many datasets within 100 iterations表3 在大量数据集上100轮迭代时的AUC
(1)topkSVRG收敛速率略优于Spark Mini-Batch SGD,加速相对较差。
(2)Spark Mini-Batch SGD稳定性欠缺,并且收敛速度较慢。
(3)CoCoA、Splash等算法很难达到较高的精度。
实验3基于Real-sim数据集(低维,稀疏,N>d),实验结果如图4。通过该实验可以发现,在低维稀疏样本数多于特征维数的数据集上有以下特点:
(1)topkSVRG收敛速率相比Spark Mini-Batch SGD加速明显,尤其是在高精度范围内。
(2)Spark Mini-Batch SGD稳定性欠缺,收敛速度较慢。
(3)CoCoA、Splash等算法很难达到较高精度。

Fig.4 Experiment on Real-sim dataset图4 数据集Real-sim上的实验
实验4将本文提出的topkSVRG和Spark Mini-Batch SGD with Adadelta/Adagrad/Adam/Momentum等在不同数据集上迭代100轮时的AUC值进行对比,结果如表3所示。可以发现,在各种类型数据集上,相同迭代次数,topkSVRG性能最稳定。
4.4 实验总结
通过实验1~实验3可以发现分布式SVRG相比Spark Mini-Batch SGD结合Adadelta、Adagrad、Adam和Momentum等算法,以及CoCoA、Splash等算法在较高收敛精度要求下,收敛加速效果明显。通过实验4可以发现topkSVRG是一个相对稳定的算法,模型准确率相对较高。
5 结束语
采用top-k局部模型平均来更新全局模型的思想,本文设计实现了分布式SVRG算法topkSVRG,用于求解大规模分布式机器学习最优化问题;基于Spark平台进行实现,并理论分析了topkSVRG的线性收敛性;实验表明topkSVRG优于目前Spark支持的Mini-Batch SGD算法,尤其是在高精度范围内可以取得明显的加速效果。此外,topkSVRG鲁棒性比较好,在稀疏数据集、稠密数据集上都可以取得不错的加速效果。
对于训练样本小于特征维数的情况(N≤d),topkSVRG还存在一些不足,相比Spark Mini-Batch没有太大优势。下一步针对样本数少于特征维数的情况进行算法优化,并进一步完善理论证明。此外,将topkSVRG应用于深度学习场景并进行优化。
