基于modeFRONTIER软件的空气动力学多目标智能优化
2018-07-13刘欢韩思远李飞
刘欢 韩思远 李飞
(华晨汽车工程研究院)
汽车空气动力学性能对汽车的动力性、经济性及操稳性等有着重要的影响,降低气动阻力可以显著改善汽车的动力性和经济性,降低气动升力有助于提升汽车的操稳性能。在满足结构设计、美学、人体工程学及法规要求的同时,降低气动阻力的设计空间不断缩小,降低气动升力的方法又常常与降低气动阻力的方法产生冲突,如何平衡二者是工程师面临的挑战。国内对飞行器、高速列车及风机领域空气动力学多目标优化关注较多,在汽车行业,文献[1]基于智能算法对汽车气动外形参数进行了多目标优化,在其他设计目标满足要求的条件下成功地将阻力系数降低了9.5%。当前的研究较多应用了Kriging近似模型,此模型在处理非线性问题时与神经网络对比其精度有明显劣势,故文章选择神经网络搭建近似模型,精度高,可以大幅节约计算成本,同时使用此近似模型进行多目标遗传算法优化,可以快速达到Ahmed模型[2]气动阻力和升力最优化。
1 仿真模型
Ahmed模型在汽车空气动力学研究过程中发挥了重要的作用,许多论文基于此模型展开研究,其试验数据更是研究的强有力支持,因此,文章亦将此模型作为研究对象。
1.1 模型简介
Ahmed模型是由AHMEDS等人在1984年为研究汽车尾涡而设计的,其前端具有类似汽车的钝体特征,模型的尾部变形可以产生多种不同尾涡流场,对Ahmed模型开展尾部变形和尾部流场的研究具有重要意义。Ahmed模型尺寸为1 044 mm×389 mm×288 mm,前端倒角半径为100 mm,离地间隙为50 mm。Ahmed模型尺寸,如图1所示[3]。

图1 Ahmed模型尺寸图
1.2 参数定义
ANSA软件是CFD仿真过程中常用的前处理软件,其Morph变形模块可以对模型进行参数化自动变形。文章利用modeFRONTIER软件在后台关联ANSA软件控制变形参数的变化,对Ahmed模型进行参数化变形后,自动输出变形结果的网格文件。
本研究拟对Ahmed模型尾部上方(Angle_top)、尾部下方(Angle_bottom)及尾部两侧(Angle_side)变形进行研究。尾部上方、下方及两侧变形量分别为0~30°,0~10°,0~10°,变形位置,如图2所示。
1.3 仿真模型标定

图2 Ahmed模型变形参数位置示意图
本研究采用STARCCM+软件进行CFD求解计算,对于 Ahmed 基础模型(Angle_top=0°,Angle_side=0°,Angle_bottom=0°)进行CFD仿真计算,计算模型计算域入口到Ahmed模型前距离为3倍车长,计算域出口距Ahmed模型后端7倍车长,计算域入口尺寸3 m×3 m,阻塞比约为1.28%,满足工程分析对阻塞比要求。CFD模型体网格总数约为1 200万个。本研究CFD求解选用Realizablek-ε模型进行稳态分析。阻力系数仿真结果为0.253,试验结果为0.25,绝对误差为0.003。仿真与试验结果的误差小于3%。认为本研究中CFD仿真方法精度满足智能优化流程计算,基于上述模型的CFD仿真求解设置可以应用整体自动化优化流程求解。
2 优化方法
2.1 理论基础
试验设计采用modeFRONTIER中的优化拉丁超立方设计方法,优化拉丁超立方设计使所有的试验点尽量均匀地分布在设计空间,具有很好的空间填充性和均衡性。优化拉丁超立方设计改进了随机拉丁超立方设计的均匀性,使因子和响应的拟合更加精确真实。
神经网络模型呈现着高度的非线性,同时,神经网络能够处理连续的模拟信号以及不精确和不完全的模糊信息,这使得神经网络给出的通常是满意解而非精确解。神经网络可以经过一段时间的训练或感知,对给定的输入产生期望的输出,因此,神经网络具有自学习、自组织及自适应性。神经网络的上述特点,使得它在优化计算中取得了较好的应用效果[4]。
本研究采用modeFRONTIER中的多目标遗传算法(MOGA-II),MOGA-II是多目标遗传算法的专有版本,它使用智能高效的多搜索精英法,能够保持优秀(帕雷托解或非劣解)的解决方案,而不会过早地收敛到局部最优。精英法改进了算法的收敛性,并确保每新一代的适应度大于父代的适应度[5]。
2.2 优化流程
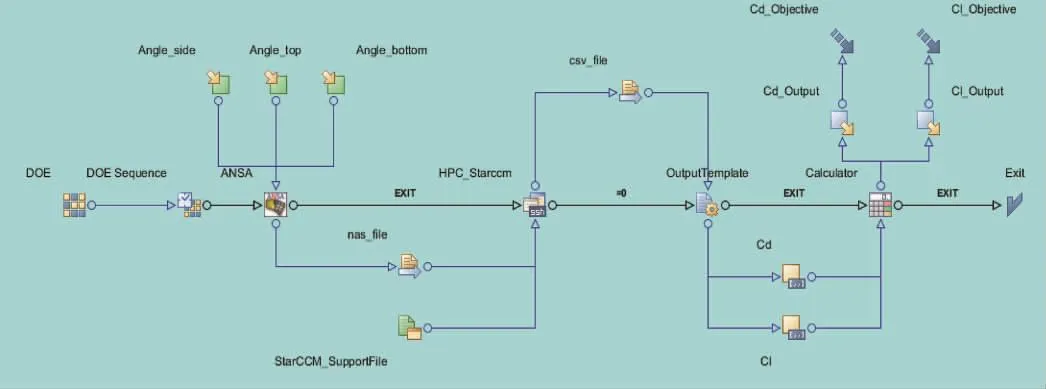
本研究拟通过试验设计(DOE)优化拉丁超立方的方法对不同的参数组合选取足够数量的样本点进行CFD仿真计算,计算给出风阻系数和升力系数数值,基于计算结果通过神经网络近似模型构建参数与目标(风阻系数、升力系数)之间的关系,基于此近似模型继续应用多目标遗传算法进行寻优。Ahmed模型智能优化流程,如图3所示。

图3 Ahmed模型智能优化流程图
本研究应用优化拉丁超立方方法选取总计130个样本点,基于计算结果利用神经网络分别对阻力和升力系数构建近似模型,对近似模型进行R2检验,当R2>0.9时,认为近似模型精度满足使用要求。建立近似模型后,基于此近似模型选择多目标遗传算法寻优。多目标遗传算法进行了100代进化,基于近似模型的计算量为22 000余次,计算时间约3 min。
3 结果分析
3.1 参数分析
通过对参数进行分析,Ahmed模型3组参数中尾部两侧变形对风阻系数影响最大;尾部上方和尾部下部变形对升力系数影响最大。其中,风阻系数随着尾部两侧角度增大而降低,升力系数随着尾部上方角度增大而升高,升力系数随着尾部下方角度增大而降低。参数与目标关系,如图4和图5所示。

图4 参数变化对风阻系数影响主效应图

图5 参数变化对升力系数影响主效应图
3.2 近似模型分析
DOE计算完成后,基于计算结果利用神经网络分别对风阻和升力系数构建近似模型,通过R2检验,利用神经网络对风阻系数构建的近似模型进行R2检验,得R2=0.984;利用神经网络对升力系数构建的近似模型进行R2检验,得R2=0.999,均大于检验标准0.9,认为二者近似模型精度满足使用要求。
3.3 优化结果分析
对于风阻和升力系数,基于各自的神经网络近似模型选择多目标遗传算法寻优后,得出帕雷托前沿,如图6所示。经过分析,认为本次寻优升力系数<0就可以接受,故选择图6中最左侧结果作为最终结果。
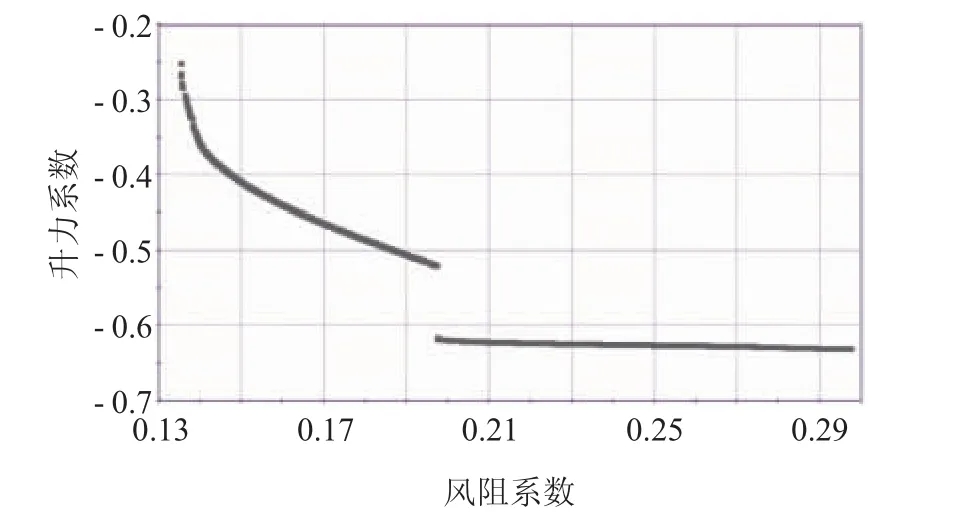
图6 Ahmed模型多目标优化帕雷托前沿图
Ahmed模型利用多目标遗传算法基于神经网络近似模型的优化结果,如表1所示。

表1 Ahmed模型最优结果
将优化结果与基础模型对比,生成Y=0截面湍动能损耗云图,如图7所示。由图7对比可知,经过尾部优化后,Ahmed模型尾涡区明显减小,优化效果明显。

图7 Ahmed模型优化前后Y=0截面湍动能损耗对比图
Ahmed模型表面压力系数云图对比,如图8所示。通过图8对比可知,经过尾部优化后,Ahmed模型尾部压力明显升高,优化效果明显。
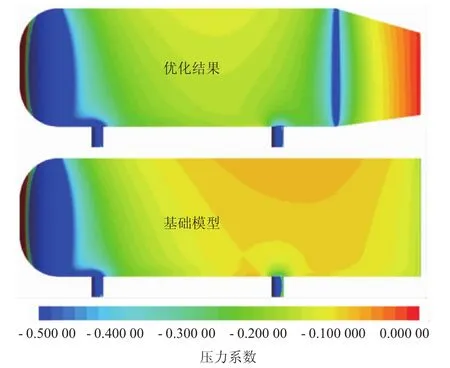
图8 Ahmed模型表面压力系数云图
3.4 结果验证
因基于近似模型求解的最优结果与CFD仿真求解结果存在误差,故本研究对基于近似模型求解得出的最优参数进行CFD计算验证。验证结果为风阻系数误差-1.7%,升力系数误差4.0%。对比结果,如表2所示。
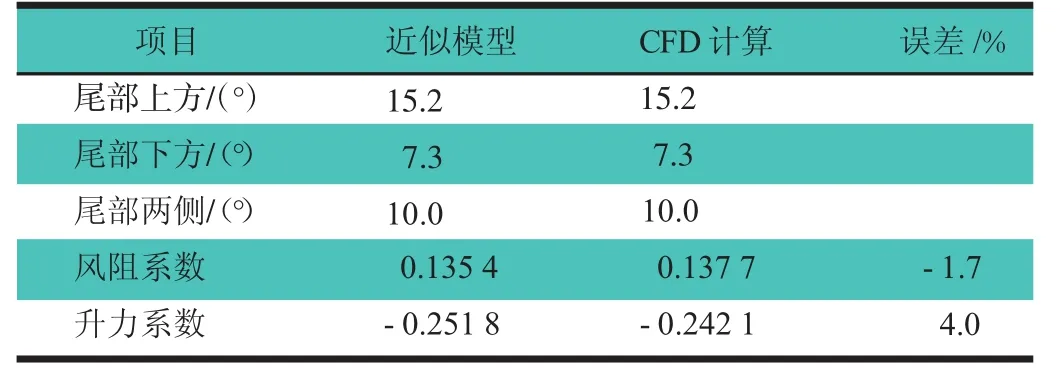
表2 Ahmed模型最优结果验证对比
4 结论
本研究讨论了Ahmed模型尾部上方、下方和两侧角度的改变对空气动力学性能的影响,通过分析可知,风阻系数随着Ahmed模型尾部两侧角度增大而降低,升力系数随着Ahmed模型尾部上方角度增大而升高,升力系数随着Ahmed模型尾部下方角度增大而降低。本次优化风阻系数降低了46.6%,升力系数降低了36.5%。
文章给出了多目标智能优化的方法,基于mode-FRONTIER搭建了智能优化流程,利用神经网络近似模型构建了参数与风阻系数和升力系数2个目标的关系,在此基础上,使用多目标遗传算法进行了优化,经过CFD验证,基于近似模型的优化精度较高,对工程应用有着重要的指导意义。
