基于最大后验贝叶斯法的临床药动学采样点优化研究的文献分析

何子剑　詹莹　邵华　于锋

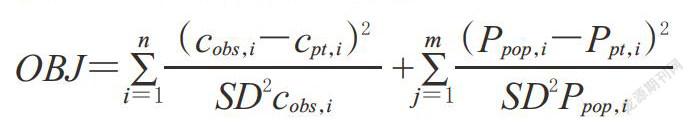
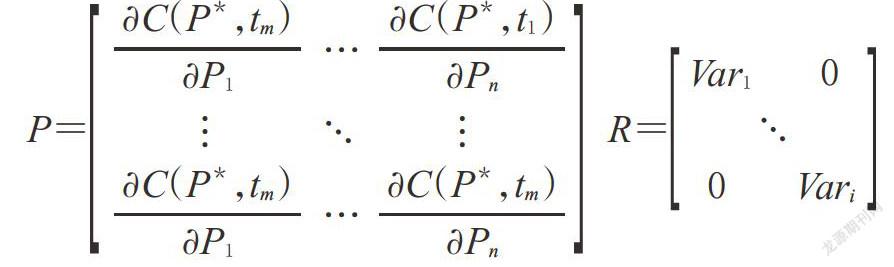
中圖分类号 R969.1 文献标志码 A 文章编号 1001-0408（2018）02-0210-06

DOI 10.6039/j.issn.1001-0408.2018.02.16

摘 要 目的：为临床药动学采样点优化研究提供参考。方法：以“贝叶斯估计”“贝叶斯反馈法”“有限采样”“优化采样”“稀疏采样”“最小采样”和“Bayesian estimate（s）”“Bayesian estimator（s）”“Bayesian analysis”“Limited sampling”“Optimal sampling”“Sparse sampling”“Minimal sampling”等为检索词，组合查询2011年1月-2016年6月在中国知网、万方、维普和PubMed、Medline、ScienceDirect等数据库中有关药动学采样点优化研究方面的文献，并对其进行系统分析与评价。结果：最终纳入中文文献1篇、英文文献13篇。有关临床药动学采样点优化研究方面的药物，主要集中在免疫抑制剂、抗病毒药物、抗菌药物和儿童个体化用药等领域。目前，关于临床药动学优化采样策略的研究方法国内仍较多采用多元线性回归法（MLR），国外已广泛应用最大后验贝叶斯法（MAPB）。MLR方程简便易用，但对采样点要求十分严格；MAPB法可应用较少采样点完成，且对采样时间要求少，更适于临床实践，但需要应用专业软件完成。两种方法精密度和准确度大致相同。优化采样策略的研究方法差异较大，但均包含获取先验信息、确定参考值、优化采样点、验证预测能力4个步骤。结论：MAPB法结果准确、可靠，且对采样点要求更少，更符合临床实践需要，适用于临床药动学优化采样研究。

关键词 最大后验贝叶斯法；多元线性回归法；优化采样策略；治疗药物监测；药动学；群体药动学

ABSTRACT OBJECTIVE： To provide reference for the study of optimal sampling points in clinical pharmacokinetics. METHODS： The literatures about optimal sampling points in clinical pharmacokinetics were searched from CNKI， Wanfang database， VIP， PubMed， Medline， ScienceDirect and other databases during Jan. 2011-Jun. 2016 using “Bayesian estimate（s）”“Bayesian estimator（s）”“Bayesian analysis”“Limited”“Optimal”“Sparse”“Minimal sampling” as retrieval words. The systematic analysis and evaluation were conducted. RESULTS： A total of 1 Chinese literature and 13 English literatures were involved respectively. The drugs they focused on were mainly immunosuppressive agents，antiviral drugs， antibiotics， pediatric individualized medication， etc. Multiple linear regression （MLR） was still the most widely used method in China，while maximum a posteriori Bayesian （MAPB） method was more popular in foreign studies. MLR equation was simple and easy to use， but the sampling was very strict. MAPB method could be completed with less sampling points and sampling time； it was more suitable for clinical practice， but needed professional software. The precision and accuracy of the two methods were similar. The research methods of optimal sampling strategy were quite different but all included 4 steps as prior information ganining， reference value determination， sampling point optimization， prediction capability verification. CONCLUSIONS： MAPB method requires less sampling points and it results are relatively accurate and reliable. It is more suitable for clinical practice and optimal sampling study of clinical pharmacokinetics.

KEYWORDS Maximum a posteriori Bayesian； Multiple linear regression； Optimal sampling strategy； Therapeutic drug monitoring； Pharmacokinetics； Population pharmacokinetics

随着药动学（PK）研究的逐步深入，特别是临床药理学的发展，治疗药物监测（TDM）越来越多地应用群体药动学（PPK）模型，即将日常收集的患者血药浓度信息按照PPK研究方法建模，然后依据模型计算个体PK参数，并预测患者给药后的血药浓度，再根据TDM得到患者的实际血药浓度值，调整给药剂量和频次使血药浓度位于目标范围内，从而达到精准治疗的目的。目前，TDM已在多种药物治疗中开展，包括免疫抑制剂[1-2]、抗肿瘤药物[3]和抗菌药物[4-5]等。

通过TDM对患者的治疗药物进行剂量制订和调整，通常需要估算1个或多个PK参数，由此确定药物的暴露量，再据此调整药物的用法用量。由于大多数药物的暴露量无法直接测得，因此需要选取与其相关性良好的指标，谷浓度即是其一[1]。然而，单一谷浓度点的个体差异性较大，仅通过谷浓度确定治疗窗、调整给药方案的方法逐渐受到质疑。与选取单一谷浓度为监测指标的方法相比，选取多个采样点为指标可显著减少药物治疗不当情况的发生[6]。近年来，越来越多的学者认为，药-时曲线下面积（AUC）与疗效和毒性反应的相关性显著高于谷浓度，选择AUC作为监测指標能更好地反映药物治疗方案是否合理[7-8]。AUC代表药物在人体中被吸收利用的程度，可通过药-时曲线积分或梯形法（Trap）计算而得，用来表示药物的暴露量[9]；而测定稳态时的AUC，可以更好地指导临床合理用药。

按AUC的传统计算方法，通常需要采集多个时间点的血样，患者往往难以接受。因此，在确保测量结果准确的前提下，限制采样点数量具有重要的伦理学、经济学和临床意义。而PPK以最大后验贝叶斯法（MAPB）为理论基础，可以充分利用稀疏、离散的数据进行建模分析，对单个患者采样次数要求较少[3，5]。美国FDA《群体药动学指导原则》中也指出，PPK模型的建立可通过单个谷浓度值、多个谷浓度值以及多个血药浓度点（通常为1～6个）进行[10]。应用PPK模型进行采样点优化，可将原本需要密集采样的PK研究大大优化，通过极少的采样点获得较为准确的AUC值，尤其适于临床TDM实践。本研究拟通过检索中国知网、万方、维普和PubMed、Medline、ScienceDirect等数据库，统计2011年1月1日-2016年6月30日发表的临床PK优化采样研究文献并分析、比较，为后续研究提供参考。

1 研究方法

1.1 检索策略

（1）中文数据库：中国知网、万方、维普等；检索词：“贝叶斯估计”“贝叶斯反馈法”“有限采样”“优化采样”“稀疏采样”“最小采样”，单独或组合在“标题”“关键词”“摘要”中检索。（2）英文数据库：PubMed、Medline、ScienceDirect等；检索词：“Bayesian estimate（s）”“Bayesian estimator（s）”“Bayesian analysis”“Limited sampling”“Optimal sampling”“Sparse sampling”“Minimal sampling”，单独或组合在“标题”“关键词”“摘要”中检索。（3）学科范围限定：医学、药学。（4）检索时间限定：2011年1月1日-2016年6月30日。

1.2 纳入与排除标准

1.2.1 纳入标准 ①研究内容为优化采样策略（OSS）；②血药浓度数据来源于患者或临床试验受试者；③研究的药物为目前已上市或拟上市药物；④药物浓度数据来自血浆或全血样本。

1.2.2 排除标准 ①仅包含贝叶斯分析，未进行优化采样；②数据由计算机模拟产生；③优化采样采用多元线性回归法（MLR）；④药物浓度数据来源于血浆或全血以外的其他体液；⑤研究对象并非药物，而是临床检验或其他。

1.3 分析方法

记录每篇文献所研究的药物、优化软件、建模患者例数、PPK模型构建方法、采样点优化方法、预测能力评价指标、OSS验证方法，并由检索得到的文献总结出OSS的必备步骤。笔者进行系统评价时，由于不同研究的方法差异较大，建模软件、研究药物与目标人群也存在较大差异，未能采用统一的统计学方法进行比较，故未进行Meta分析。

2 结果

经初步检索，共得到中文文献17篇、英文文献67篇；进一步按照“1.2”项下纳入与排除标准进行筛选，最终纳入中文文献1篇、英文文献13篇；再按照OSS研究步骤对文献进行分析。OSS研究通常包含4个步骤，即获取先验信息、确定参考值、优化采样点、验证预测能力，检索结果见表1（注：“PPK分析方法”项下，MEM表示非线性混合效应模型法，ITSB表示迭代两步贝叶斯分析法；“参考值计算方法”项下，BFS表示贝叶斯全抽样法，MC表示蒙特卡罗模拟法；“预测能力评价指标”项下，RMSE表示均方根误差，PE表示相对误差，MPE表示平均相对误差，AE表示相对误差绝对值，MAE表示平均相对误差绝对值，R2表示判定系数）。

2.1 OSS模型的构建方法

医院药学研究常常受到伦理学和受试者病理、生理状态等因素的制约，很难像普通PK研究一样可以通过密集采样来进行PK参数的估算。对于临床实践而言，如何应用较少的采样点获得准确的PK参数显得至关重要[20]。通过检索文献，笔者发现目前的OSS研究多采用MLR法和MAPB法，国内研究普遍采用MLR法，该检索条件下仅有1篇MAPB法研究[18]纳入分析，而国外研究则广泛采用MAPB法。下面将分别进行介绍。

2.1.1 MLR法 MLR法是估算药物PK参数或药物暴露量的经典方法。该方法需要按照传统PK研究方法对患者进行密集采样，通常采集8～12个点[18]。将上述各点血药浓度应用Trap法计算出实测AUC（Observed AUC），再按照MLR方程得到估算AUC（Estimated AUC），并比较两者是否一致。MLR方程[21]可表示如下：

AUC=A0+A1×c1+A2×c2……+An×cn

式中，A0是Y轴截距，cn是tn时间点对应的血药浓度，An是MLR的相关系数。

采用MLR法的优势在于方程简便易用，不需要复杂的数学建模方法，而且易于理解，仅需通过利用简单的统计软件即可完成分析。但是该方法也存在一定的不足，就是只能严格按照事先设计的采样方案加以应用，在临床实践过程中，若患者因为各种原因缺失任何一个采样点，那么该方法建立的回归方程和先验数据都将失效，故灵活性较差。

2.1.2 MAPB法 近年来，MAPB法越来越多地被应用于估算药物的PK参数，由表1检索结果可知，国外研究已广泛采用这一方法。该方法基于贝叶斯定理，即先验信息与观察值之间存在必然联系。MAPB法中的先验信息，是指与目标人群相似的PPK参数分布，通常包含均值、方差、协方差等信息；观察值是指目标患者的血药浓度及其他个体信息，如年龄、体质量、肌酐清除率等。其目标函数值可用方程表示如下：

OBJ=[∑][i=1][n][（cobs，i-cpt，i）2

SD2cobs，i] +[∑][j=1][m][（Ppop，i-Ppt，i）2

SD2Ppop，i]

式中，OBJ代表目標函数值，即评判模型拟合效果的标尺；n代表血浆样品数量；m代表参数的数量；Ppop和Ppt分别代表PPK参数和个体PK参数；cobs表示实测血浆药物浓度；cpt表示预测浓度；SD2Ppop表示PPK模型估算参数的方差；SD2cobs表示血药浓度观察值的方差。该方法的总残差由以下3个部分组成[10]：①PK模型设定误差；②给药剂量、给药时间、采样时间误差；③测量误差。通常，假定PK模型误差小至可忽略不计，同时通过严格控制给药和采样时间以减小误差，因此误差主要来源于测量、分析及失误。

采用MAPB法的主要优点在于药物的PK参数可通过任意时间点、任意数量的血样进行估算[18]。该方法估算准确度主要与采血时间点和数量多少有关，所有先验信息都可加入方程。相比MLR法，MAPB法对数据的利用度更高。该方法的缺点是对数学及统计学基础要求较高，进行研究需要应用专业的PPK软件，需要学习一定的编程语言。

MLR法与MAPB法建立OSS拟合AUC的精密度和准确度较为接近。有研究指出，MAPB法较MLR法更具灵活性，即使患者漏采1次血样或采样时间与原定时间差别较大，都不会对拟合结果产生显著影响[18]，因此更利于临床操作实施。目前，国内与药物PK相关的OSS研究仍多采用MLR法，不过MAPB法也逐步得到了应用。

2.2 获取先验分布

先验分布是PPK模型的重要组成部分，通常是由观察结果或实验数据组成的数据集，包含患者的基本信息（如年龄、体质量、肌酐清除率等），以及1个或多个时间点对应的血药浓度。PPK模型研究方法通常分为两种：参数法和非参数法。参数法假定PPK参数有特定分布，通常呈正态分布或对数正态分布；非参数法则无需作假设。OSS通常由以下几种较为明确的方法进行PPK模型建立：（1）标准两步法（STS）；（2）MEM；（3）ITSB；（4）非参数最大期望值法（NPEM）[3]。

2.3 确定参考值

为了评估模型的预测性能，需要确定特定的PK参考值。参考值的计算方法通常有以下几种：Trap法、BFS法、非线性最小二乘回归估算法（NLR）、MC法。

大部分研究均以AUC作为PK参考值[7-8]，根据各采样点对应的血药浓度值，用Trap法即可计算出参考AUC。如果研究关注AUC之外的其他参数（如清除率）[10]，那么Trap法便不再适用，通常可采用另外3种方法。BFS法[6]、NLR法[22]均假设其结果与实测值十分接近，若模型拟合值与实测值差距过大，那么模型预测结果的偏差也会很大。MC法可以作为一种评估模型预测性能的方法[22]，按照PPK模型随机抽样产生虚拟患者，以此模拟出足够的样本量来表现整体分布情况。在这些虚拟患者中，给药剂量和药-时曲线都可以模拟产生。这些患者的PK参数确切可知，并且可以作为较少样本量时MAPB法的参考值。

2.4 确定优化采样点

应用优化的采样点估算个体PK参数时，结果可能会不完全精确。为了提高估算的精度，通常可采用OSS的方法来进行采样点的选择。文献中较常采用的方法有D优化法[10]、ED优化法和全部组合测验方法[3]。OSS的理念如下：特定采样时间点对于某一PK参数的影响远大于其他时间点。不同采样点对于预测结果的影响程度，可通过Fisher信息判断，它表示观测数据蕴含的信息量[23]，反映对参数估算的准确程度。Fisher信息越大，对参数估算的准确度越高，即代表了越多的信息量。在OSS中，Fisher信息是采样时间对应的1个或多个PK参数的信息量。D优化法中使用了Fisher信息矩阵（FIM），可通过下式确定：FIM=[PTR-1P]（式中，P表示Jacobian矩阵，PT是Jacobian矩阵的转置，R-1是测量误差的方差矩阵）。令c（P*，tm）表示在tm时P*参数下的血药浓度值，那么Jacobian矩阵可表示成N×N的形式[24]：

R矩阵中，Vari表示测量误差i的方差值；P矩阵中，?是偏微分的符号，相当于加号或减号，属于这一矩阵的计算方法，它并没有生理或药理上的意义，只是一种运算。

由于Jacobian矩阵必须是矩形矩阵，由行列式组成，故该方法要求采样点的数量不能多于参数的数量。例如，D优化法用于有2个参数（清除率和表观分布容积）的一房室模型，最多只能有2个采样点；当采样点超过参数个数时，会出现重复的采样点。

D优化法的采样点选择会受到诸多限制，不同的先验信息可能会产生不同的优化结果[25]。由于通常研究时输入的优化初始值为PPK模型均值，这一初始值的准确程度将对优化结果产生很大影响。ED优化法与D优化法类似，都是利用FIM进行优化，ED优化法可克服D优化法必须明确先验参数分布的限制[21]，但计算方法更复杂，实际应用较少。

另一種确定优化采样点的方法是全部组合测验方法，具体做法是：将每一种可能的优化采样点排列组合全部列出，分别建模比较，这种方法通常需要由临床研究或MC模拟试验设计取得的大量数据来完成。预测表现最佳的采样点组合即为最佳采样策略。然而，事实上这并不是真正的最优化，因为参与优化的时间点受到试验设计的限制。例如，研究设定每小时采样1次，那么OSS只能在这些采样点中选取1个或多个进行组合优化。

上述两种采样方法都需要建立群体模型，可对所有参数或部分参数进行优化，不同点在于：D优化法对于采样点个数有限制，全部组合测验方法则没有限制。

2.5 验证预测能力

表1中所列文献共提及了6种反应预测能力的评价指标：R2、PE、AE、MPE、MAE、RMSE。为了便于解释和比较，通常以相对值表示，分别可用以下公式表示：

上述公式中，N表示预测个数，Pi表示个体参数预测值，Ri表示个体参数真实值。

表1研究中的模型验证方法主要包括外部验证法和内部验证法两种。外部验证法采用单独的验证组比较密集采样与优化采样的参数结果，结合上述预测指标进行预测表现评价。若使用D优化法[15]确定优化采样点，样本应由单独的患者组别采取，不应在同一批患者中分出部分数据作为外部验证数据，然后应用MAPB法估算PK参数。内部验证法通过重新采样，比较建模组与验证组各均值及置信区间，若验证组均值位于建模组置信区间内，通常认为模型拟合能力较好。内部验证法常用的方法包括重采样法[16，18-19]、交叉检验法[4，11，13]等。内部验证法对患者数据利用更为高效，每个患者的数据均用于建模，同时对其进行验证。

MC法是进行模型验证的另一个有效手段，通过对PK参数分布进行模拟，可精确重现目标群体，部分文献[10，14，16]采用了这种方法。随着模拟患者的增加，这一数据集可以重现整个分布。若假设正确，模拟结果与优化采样结果比较应无统计学差异。

3 讨论

为了方便读者查阅比较，表1中列出了近年来应用MAPB法进行采样点优化的典型案例。目前，MAPB法主要应用于免疫抑制剂（如他克莫司[2]、环孢素[8，11]）、抗病毒药物（如更昔洛韦/缬更昔洛韦[7]、阿巴卡韦等[16]）、抗菌药物（如阿尼芬净等[13]）及儿童个体化用药（如氯胺酮在儿科的应用[10]）的TDM中。这些药物大多具有治疗窗窄、需要个体化用药、密集采样较难执行等特点。应用优化采样法可以显著减少患者痛苦、增加依从性、降低治疗成本。除了用于TDM领域外，OSS还应用在基因多态性表型测定[26]、药物相互作用评价[27]、造影剂清除率测定[28]、生物等效性评价[29]等领域。

PK参数的先验分布是PPK模型的必备部分，其可靠性将直接影响OSS结果的准确性。若模型假设的PK参数分布与群体的真实分布差距较大，那么应用MAPB法将会产生较大的偏差。NONMEM是建立OSS群体模型最常用的软件，因此MEM也成为应用最广泛的方法，该方法在稀疏数据和密集数据上均有良好的表现。已有文献对有限采样策略的准确性展开探讨[30]，但偏差有多大仍不太清楚，可以作为一个课题进行深入研究。

用于MAPB法估算的参考值通常需要通过可靠的方法确定，无论是采用外部验证法还是内部验证法，产生的所有估算值均应尽可能接近真实值。BFS法应用较广，随着样本量的增加其精确度也会随之增加。Trap法用于估算AUC，在以AUC为单一优化参数的研究中常用于计算参考值。也有部分研究[9]的参考值建立在先前优化采样研究的基础上，此时应评估参考模型研究群体和自身研究群体的一致性，否则必然会存在偏差。

表1文献中使用了两种方法优化采样点。D优化法所保留的时间点可能是最具统计学信息，即Fisher信息的，但对于单一PK参数而言，因其仅考虑时间点所含统计信息量的丰富程度，并不一定是预测表现最好的；BFS法检测所有采样时间点组合的预测效果，该方法受限于预设的采样点，同时其优化结果受到预测指标的影响。

OSS验证是优化方法的重要组成部分。外部验证法是用一个单独的验证组进行外部验证，部分研究会采用这种方法。该方法需要保证验证组患者的构成与OSS模型患者类似。除了外部验证法外，当数据量充足时，重采样法也可用于采样策略的验证。同时，若患者数据有限，仅能建立PPK模型时，可采用MC进行验证。这些方法在表1所列文献中均有应用。

4 结语

MAPB法是一种精确、通用、灵活的方法，其预测表现与MLR法类似。目前国内应用较多的是MLR法。相比较而言，MAPB法的原理较难理解，同时需要采用NONMEM等软件进行操作，难度较大，但其对采样点要求更少，从临床实际应用的角度来看，该方法显然更符合临床实践需要。本研究通过对近年来的OSS研究进行检索总结，希望为后续相关研究提供借鉴。文中涉及较多统计学与数学建模方面的概念、理论未能全面阐述，希望今后会有更多的医院药学工作者投入到定量药理学的研究领域，将药学知识服务于临床。

参考文献

[ 1 ] SAREM S，NEKKA F，BARRI?RE O， et al. Limited sampling strategies for estimating intravenous and oral cyclosporine area under the curve in pediatric hematopoietic stem cell transplantation[J]. Ther Drug Monit，2015，37（2）：198-205.

[ 2 ] ANDREU F， COLOM H， GRINY? JM， et al. Development of a population PK model of tacrolimus for adaptive dosage control in stable kidney transplant patients[J]. Ther Drug Monit，2015，37（2）：246-255.

[ 3 ] WATANABE M， FUKUOKA N， TAKEUCHI T， et al. Developing population pharmacokinetic parameters for high- dose methotrexate therapy：implication of correlations among developed parameters for individual parameter estimation using the Bayesian least-squares method[J]. Biol Pharm Bull，2014，37（6）：916-921.

[ 4 ] DIJKSTRA JA， VAN ALTENA R，AKKERMAN OW， et al. Limited sampling strategies for therapeutic drug monitoring of amikacin and kanamycin in patients with multidrug-resistant tuberculosis[J]. Int J Antimicrob Agents，2015，46（3）：332-337.

[ 5 ] MAGIS-ESCURRA C， LATER-NIJLAND HMJ， ALFFENAAR JWC， et al. Population pharmacokinetics and limited sampling strategy for first-line tuberculosis drugs and moxifloxacin[J].Int J Antimicrob Agents，2014，44（3）：229-234.

[ 6 ] WILHELM AJ，DE GRAAF P，VELDKAMP AI， et al. Po- pulation pharmacokinetics of ciclosporin in haematopoietic allogeneic stem cell transplantation with emphasis on limited sampling strategy[J]. Br J Clin Pharmacol，2012，73（4）：553-563.

[ 7 ] CALD?S AP， COLOM H， CALDES A， et al. Optimal sparse sampling for estimating ganciclovir/valganciclovir AUC in solid organ transplant patients using NONMEN[J]. Ther Drug Monit，2014，36（3）：371-377.

[ 8 ] FRUIT D， ROUSSEAU A， AMREIN C， et al. Ciclosporin population pharmacokinetics and Bayesian estimation in thoracic transplant recipients[J]. Clin Pharmacokinet，2013，52（4）：277-288.

[ 9 ] SUN HE，FADIRAN EO，JONES CD， et al. Population ph- armacokinetics[J]. Clin Pharmacokinet，1999，37（1）：41- 58.

[10] SHERWIN CM， STOCKMANN C， GRIMSRUD K， et al. Development of an optimal sampling schedule for children receiving ketamine for short-term procedural sedation and analgesia[J]. Paediatr Anaesth，2015，25（2）：211-216.

[11] SAREM S，LI J，BARRIERE O， et al. Bayesian approach for the estimation of cyclosporine area under the curve using limited sampling strategies in pediatric hematopoietic stem cell transplantation[J]. Theor Biol Med Model，2014，11（1）：39.

[12] ZHAO W，FAKHOURY M，BAUDOUIN V， et al. Limited sampling strategy for estimating individual exposure of tacrolimus in pediatric kidney transplant patients[J]. Ther Drug Monit，2011，33（6）：681-687.

[13] VAN WANROOY MJ，PROOST JH，RODGERS MG， et al. Limited-sampling strategies for anidulafungin in critically ill patients[J]. Antimicrob Agents Chemother，2015，59（2）：1177-1181.

[14] YOUSEF AM， MELHEM M， XUE B， et al. Population pharmacokinetic analysis of clopidogrel in healthy Jordanian subjects with emphasis optimal sampling strategy[J]. Biopharm Drug Dispos，2013，34（4）：215-226.

[15] MONCHAUD C， DE WINTER BC， KNOOP C， et al. Population pharmacokinetic modelling and design of a Bayesian estimator for therapeutic drug monitoring of tacrolimus in lung transplantation[J].Clin Pharmacokinet，2012，51（3）：175-186.

[16] ZHAO W，CELLA M，DELLA PASQUA O， et al. Population pharmacokinetics and maximum a posteriori probability Bayesian estimator of abacavir：application of individualized therapy in HIV-infected infants and toddlers[J]. Br J Clin Pharmacol，2012，73（4）：641-650.

[17] ZHAO W， MAISIN A， BAUDOUIN V， et al. Limited sampling strategy using Bayesian estimation for estimating individual exposure of the once-daily prolonged-release formulation of tacrolimus in kidney transplant children[J]. Eur J Clin Pharmacol，2012，69（5）：1181-1185.

[18] 丁俊杰，焦正，王藝.基于D最优设计的最大后验贝叶斯法估算个体药动学参数[J].药学学报，2011，46（12）：1493-1500.

[19] CASTRO FA， PIANA C， SIM?ES BP， et al. Busulfan dosing algorithm and sampling strategy in stem cell transplantation patients[J]. Br J Clin Pharmacol，2015，80（4）：618-629.

[20] 左笑丛，袁洪，张毕奎，等.用模型和模拟方法设计氨氯地平的群体药动学研究方案[J].药学学报，2012，47（7）：941-946.

[21] NIIOKA T，MIURA M，KAGAYA H， et al. A limited sampling strategy to estimate the area under the concentration-time curve of tacrolimus modified-release once-daily preparation in renal transplant recipients[J].Ther Drug Monit，2013，35（2）：228-232.

[22] MCDOUGALL DA， MARTIN J， PLAYFORD EG， et al. Determination of a suitable voriconazole pharmacokinetic model for personalised dosing[J]. J Pharmacokinet Pharmacodyn，2015，43（2）：165-177.

[23] 孙鹤，施心陵，赵磊，等.基于D-优化设计的那拉曲坦给药方案的建模与仿真[J].生物医学工程研究，2012，31（4）：238-240.

[24] DARGENIO DZ. Optimal sampling times for pharmacokinetic experiments[J]. J Pharmacokinet Biopharm，1981，9（6）：739-756.

[25] 付东晓，张蕊，李芳，等.不同先验信息下D-优化法的估值精度及其适用性[J].含能材料，2009，17（3）：339-343.

[26] DE ANDR?S F，TER?N S，BOVERA M， et al. Multiplex phenotyping for systems medicine：a one-point optimized practical sampling strategy for simultaneous estimation of CYP1A2，CYP2C9，CYP2C19，and CYP2D6 activities using a cocktail approach[J]. OMICS，2016，20（2）：88-96.

[27] DUMORTIER T，LOOBY M，LUTTRINGER O， et al. Estimating the contribution of everolimus to immunosuppressive efficacy when combined with tacrolimus in liver transplantation：a model-based approach[J]. Clin Pharmacol Ther，2015，97（4）：411-418.

[28] BENZ-DE BRETAGNE I， LE GUELLEC C， HALIMI JM， et al. New sampling strategy using a Bayesian approach to assess iohexol clearance in kidney transplant recipients[J].Ther Drug Monit，2012，34（3）：289-297.

[29] CHEN LF， JIAO JJ， ZHANG CL， et al. Bioequivalence assessment of metformin hydrochloride using a limited sampling strategy[J]. Int J Clin Pharmacol Ther，2011，49（10）：629-636.

[30] ADD RAHMAN AN，TETT SE，STAATZ CE. How accurate and precise are limited sampling strategies in estimating exposure to mycophenolic acid in people with autoimmune disease？[J]. Clin Pharmacokinet，2014，53（3）：227-245.

（收稿日期：2017-02-07 修回日期：2017-07-20）

（编辑：杨小军）