不确定非线性系统的事件驱动鲁棒跟踪控制
2018-07-12崔黎黎王晓薇
崔黎黎, 王晓薇, 吴 鹏, 王 利
(沈阳师范大学 科信软件学院, 沈阳 110034)
在实际工业领域中,大多数被控对象具有高度非线性,很难获得其精确的数学模型,这使得实际动态系统和系统的数学模型间普遍存在不确定性,从而导致系统的性能变差甚至不稳定,因此,控制器设计时鲁棒性是研究者们所考虑的重点。非线性鲁棒跟踪控制研究如何设计控制器使系统在不确定性作用下能够跟踪一个给定的目标轨迹,一直是控制领域研究的一个重点内容。研究者们基于经典的控制理论,如变结构控制[1]、模型预测控制[2]、反演控制[3]、神经网络控制[4]等,提出了各种鲁棒跟踪控制方法。然而,上述方法虽然实现了鲁棒跟踪,但大多数未考虑系统性能的优化。
近年来,自适应动态规划方法(adaptive dynamic programming, ADP)由于具有自学习与优化能力,能够有效解决动态规划的“维数灾”问题,现已成为了控制领域研究的热点。 目前ADP理论在非线性系统的最优控制[5]、微分对策[6]、多智能体系统的最优控制[7]等方面已取得了许多重要的研究成果。在最优跟踪控制方面,文献[8]针对一类不确定连续非线性系统提出了基于评价网络-控制网络结构的神经网络自适应鲁棒器设计方法。文献[9]基于ADP方法研究了一类不确定离散非线性系统的鲁棒跟踪控制问题。文献[10]提出了一个在线策略增强学习算法,实现了一类未知非线性系统的H∞跟踪控制。文献[11]针对一类未知不确定性系统的跟踪控制问题提出了一个数据驱动ADP算法。然而,上述控制器设计方法均未考虑网络带宽的限制,所设计的控制器是基于时间驱动的,采用实时更新的方式,因此网络负荷和计算量较大,在实际应用中具有一定的局限性。据作者所知,目前基于ADP的不确定非线性系统的事件驱动鲁棒跟踪控制相关结果尚未见报道。
本文针对一类非线性系统提出一种基于事件驱动自适应动态规划方法的鲁棒跟踪控制方案。首先,利用系统增广技术将原系统转化为由跟踪误差和目标轨迹表示的增广系统,从而将原系统的鲁棒跟踪问题转化为增广系统的鲁棒镇定问题。为了处理不确定性的同时优化系统跟踪性能,定义了一个新的性能指标函数,进一步将增广系统的鲁棒镇定问题转化为其标称系统的最优控制问题,推导得出相应的HJB方程和最优控制策略,并在理论上证明了问题转化的等价性。针对标称系统,提出了一个事件驱动自适应动态规划算法设计近似最优控制策略,值得指出的是该控制策略仅在事件触发时刻更新,可大大减少网络负载和计算量。利用Lyapunov稳定性理论严格证明了闭环系统的一致最终有界稳定性。仿真例子验证了所提出的控制方案的有效性。
1 问题描述
考虑如下的不确定非线性系统:
(1)
其中:x(t)∈Rn为系统状态;u(t)∈Rm为系统控制输入;d(t)∈Rm为控制扰动。假设f(x(t))和g(x(t))满足Lipschiz连续性条件,且系统在Ω∈Rn是强可控的。本文的控制目标是设计事件驱动鲁棒跟踪控制策略u(t),使得扰动存在时系统状态x(t)能够跟踪给定的目标轨迹xd(t)。假设期望轨迹满足如下的表达式
(2)
其中:xd(t)∈Rn为有界的期望轨迹;fd(xd(t))为Lipschiz连续函数,并满足fd(0)=0。
定义如下的跟踪误差
ed=x(t)-xd(t)
(3)
利用式(1)~式(3)可得系统的跟踪误差动态方程为
(4)
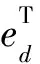
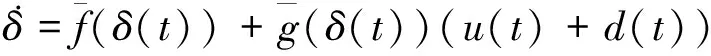
(5)
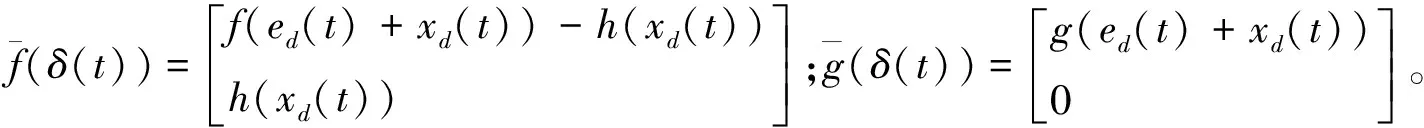
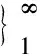
∀t∈[tk,tk+1)
(6)
则当t=tk时,有ek(tk)=0。基于状态采样的事件驱动控制策略可表示如下
∀t∈[tk,tk+1)
(7)
由式(7)可知事件驱动控制策略仅在事件触发条件满足时更新,而在2个相邻的事件间则保持不变。控制输入的连续性可由零阶保持器保证。接下来,本文将针对增广系统(5)在事件驱动控制框架下提出一个基于ADP方法的事件驱动鲁棒控制策略,从而实现控制目标。
2 基于ADP的事件驱动鲁棒控制
首先,通过定义一个新的性能指标函数,进一步将增广系统的鲁棒镇定问题转化为其标称系统的最优控制问题,并在理论上证明问题转化的等价性。接着,提出一个事件驱动ADP算法求解标称系统的HJB方程,从而得到事件驱动最优控制策略。
不考虑输入扰动,增广系统(5)的标称系统可以表示为
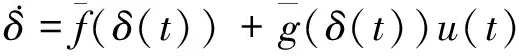
对标称系统(5),定义一个新的性能指标函数如下:
其中:λ为衰减因子;Q和R为对称正定常数矩阵。对上式求微分可得
(8)
定义Hamilton函数如下
H(δ,V(δ),u)=
(9)
最优性能指标函数V*(δ(t))定义如下:
(10)
根据Bellman最优控制原理可得,最优性能指标函数V*(δ(t))满足如下的HJB方程:

(11)
相应的最优控制策略u*(δ)为
(12)
将上式带入式(11),可得HJB方程如下:
V*(δ)=0
(13)
定理1考虑标称系统(6),定义性能指标函数为(7),控制策略为(12),假设跟踪HJB方程(13)存在一个解V*(δ(t)),若不等式:

(14)
成立,则当λ=0时,闭环系统(5)渐近稳定。当λ≠0时,闭环系统(5)一致最终有界稳定。
证明选取最优性能指标函数V*(δ(t))为Lyapunov函数,对其求导可得
(15)
由HJB方程(11)可得
(16)
根据式(12)有
(17)
利用式(16)~式(17)可得
(18)
上式两边均乘以e-λt可得
(19)
进一步可得
(20)
对上式加减dT(t)Rd(t),并利用式(14)可得
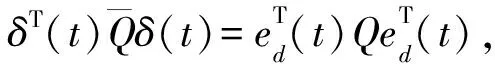
(22)
当λ≠0时,由上式可得
(23)
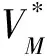
(24)
则可得闭环系统渐近稳定。证明完毕。

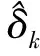
(25)
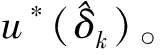
V*(δ)=W*Tσ(δ)+ε(δ)
(26)

(27)
根据式(25)和式(26)可得
(28)
(29)
将上式代入式(9)可得近似Hamilton函数:
(31)
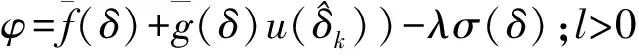
(32)
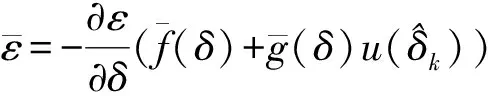
由式(6)和式(29)可得标称系统闭环动态为
(33)
3 稳定性分析
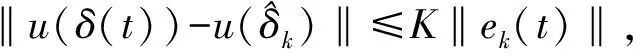
假设2g(x)有界,即‖g(x)‖≤gM,其中gM>0。
假设3评价网络理想权值W,激活函数σ(·)及其导数σ(·),近似误差ε及其导数ε均有界,即‖W‖≤WM,‖σ(·)‖≤σM,‖σ(·)‖≤σdM,‖ε‖≤εM,‖ε‖≤εdM,其中WM,σM,σdM,εM和εdM均为正常数。
定理2考虑系统(6),事件驱动控制策略为(29),评价网络权值调节律为(31)。假设系统状态满足持续激励条件,事件触发条件为
(34)
其中α∈(0,1)。若评价网络学习率l满足如下不等式
(35)
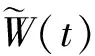
证明选取如下的Lyapunov函数
(36)
那么,当t∈[tk,tk+1)时,对Lyapunov函数(36)求导可得
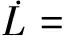
(37)
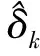
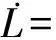
(38)
由HJB方程(13)可得
V*(δ)
(39)
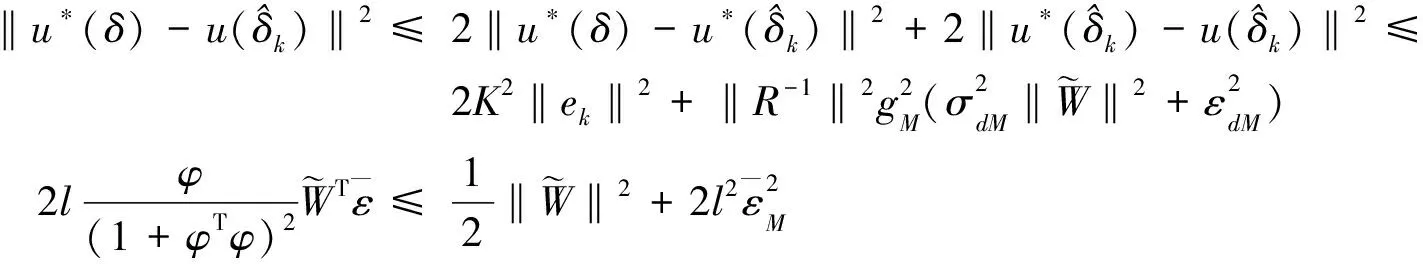
进一步可得
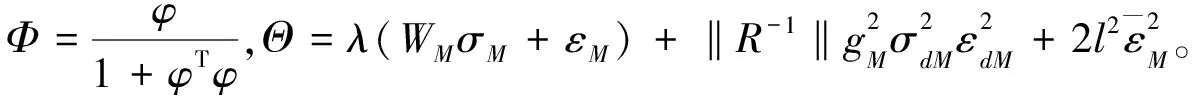
利用式(34)可得
(42)
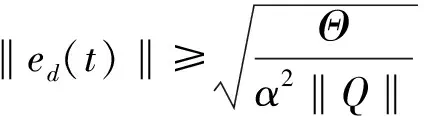
当t=tk时,对Lyapunov函数(36)求差分,
(43)
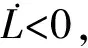
因此可得跟踪误差和神经网络权值误差均一致最终有界。证明完毕。
4 仿真例子
考虑如下的不确定非线性系统:
(44)
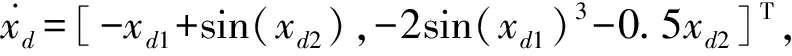
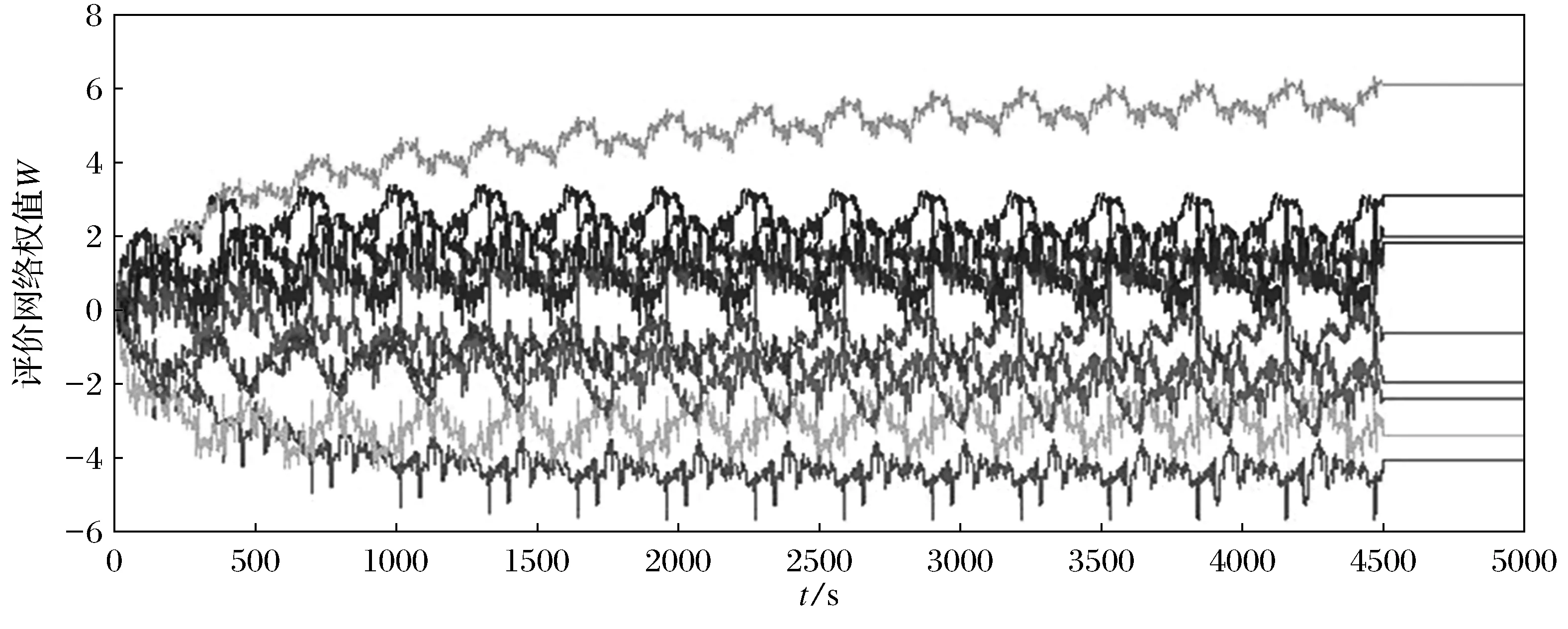
图1 评价网络的权值收敛轨迹Fig.1 Convergent trajectories of critic neural network weights
将所得到的事件驱动鲁棒控制器作用到系统(44)上,跟踪误差轨迹如图2所示,事件触发条件ek及其上界eT的轨迹如图3所示。本文提出的事件驱动的鲁棒控制器仅需更新69次,而时间驱动的控制器则需更新500次,因此可减少86.2%的计算量。仿真结果证明了本文所提出方案的有效性。
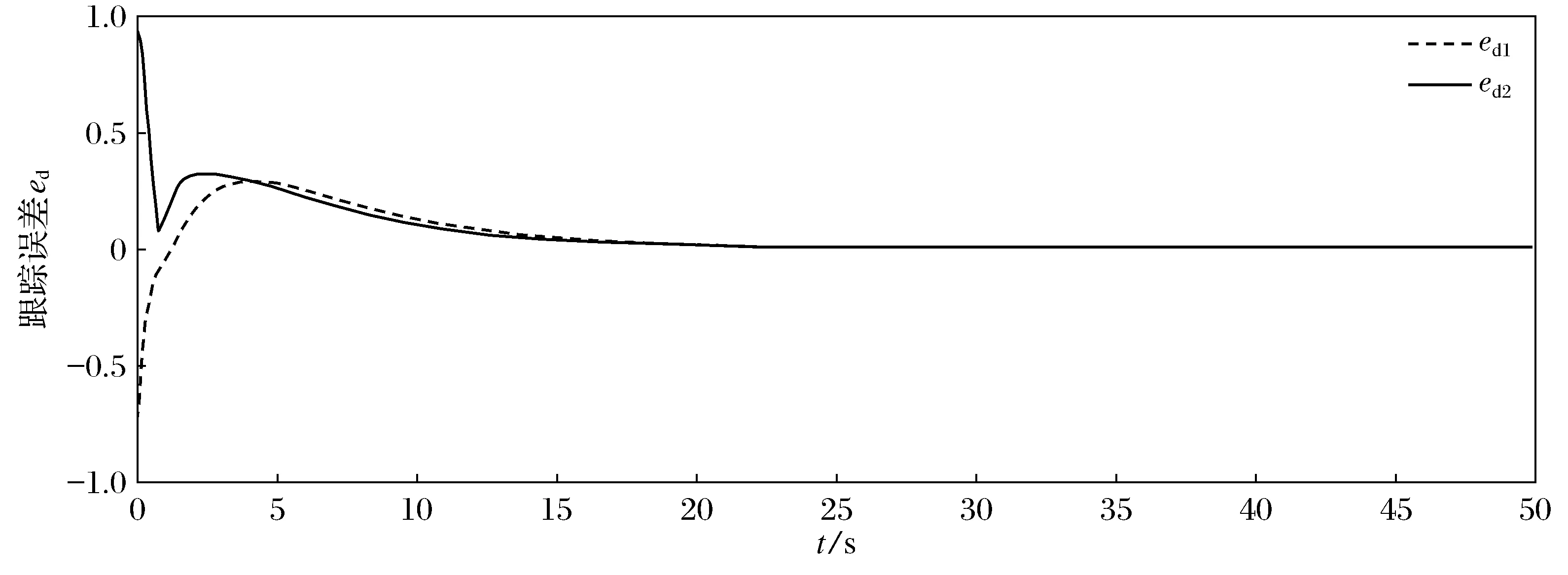
图2 跟踪误差轨迹Fig.2 Trajectories of tracking error
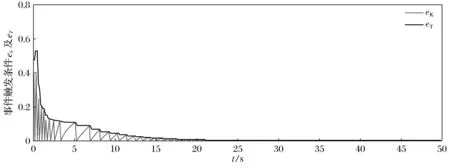
图3 事件触发条件轨迹Fig.3 Trajectories of event-triggered condition
5 结 论
针对一类不确定非线性系统的鲁棒跟踪控制问题,本文利用增广技术和引入新型性能指标函数将其转化为标称系统的最优控制问题,并结合事件驱动机制和ADP方法提出了一个事件驱动鲁棒跟踪控制方案,理论上证明了闭环系统的一致最终有界稳定性。仿真结果验证了所提出方法的有效性。
