基于遗传算法的旅游路径规划问题研究

　

(同济大学经济与管理学院　上海　201804)

一、引言

随着人们生活水平的提高，旅游已经成为人们日常生活中必不可少的一部分。科学的旅游路线设计，不仅可以有效地节约游客的时间、金钱和精力，使之充分享受到旅途的乐趣，还有助于旅游景区之间的相互对比，统筹配置。

上海便是中国举世闻名的旅游城市之一。上海位于中国东南部沿海，在长江入海口位置，是中国最发达的城市之一，也是中国的经济中心。上海密布的交通网络、繁华的街道、竞相增长的摩天大楼，都映射着这座摩天都市的不断雄起。

上海是一座极具现代化而又不失中国传统特色的都市。有超过2000万人居住和生活在这里。作为中国历史上最早的通商口岸，上海也是最早接触“外界”的地方。随着时代的变迁，上海也逐渐成为了东亚地区重要的金融贸易城市。上海是多元的，老城厢里原汁原味的老弄堂，外滩沿岸百年历史的欧式建筑，陆家嘴地区各式各样的摩天大楼，城隍庙间承载记忆的中华园林。多元的城市元素汇聚在这里，让上海独具魅力。

同济大学坐落于有着“东方巴黎”之称的上海，是教育部直属全国重点大学，国家“211工程”和“985工程”重点建设高校，在国际上享有较高的声誉。每年，都有大批的学子包括国外留学生慕名来到同济学习。上海作为一座极具现代化而又不失中国传统特色的国际大都市，拥有诸多的旅游景点，游客可以在外滩夜观美景，去城隍庙品尝美食。

对来沪求学的学生而言，在外求学获取知识的同时，领略上海当地的风土人情、游览特色景点，也是学生期间一个难忘的经历。但全日制学生因课业压力较大，时间上往往会受限制；同时经济上的预算往往也并不充足，出行选择公共交通较多。基于上述时间和经济上的限制，我们决定以遗传算法为求解算法，建立模型解决这一路线规划问题。

旅行商问题(Traveling Salesman Problem,TSP)是威廉·哈密尔顿爵士和英国数学家克克曼于19世纪初提出的一个数学问题。它是一个是典型的NP问题，其简单描述是，一名商人欲到n个城市推销商品，目标是找到一条经过所有城市且每个城市只经过一次的最短路径[1]。本文所研究的旅游路线规划问题类似于TSP问题，但不同之处在于游客要用m天游览完n个旅游景点，其中m要尽可能小，且每天必须从同一地点出发再回到该出发点，出发时间固定，返回时间不能晚于某个时刻，要求所有旅游所花费的总时间最短，也即得到了最短的天数m。

遗传算法(Genetic Algorithm,GA)是由美国Michigan大学的Holland教授于1969年提出，后经De Jong、Goldberg等人归纳总结所形成的一类模拟进化算法。它来源于达尔文的进化论、魏茨曼的物种选择学说和孟德尔的群体遗传学说。遗传算法是模拟自然界生物进化过程与机制求解极值问题的一类自组织、自适应人工智能技术,其基本思想是模拟自然界遗传机制和生物进化论而形成的一种过程搜索最优解的算法,具有坚实的生物学基础；它提供从智能生成过程观点对生物智能的模拟,具有鲜明的认知学意义；它适合于无表达或有表达的任何类函数，具有可实现的并行计算行为；它能解决任何种类实际问题，具有广泛的应用价值。因此，遗传算法广泛应用于自动控制、计算科学、模式识别、工程设计、智能故障诊断、管理科学和社会科学等领域，适用于解决复杂的非线性和多维空间寻优问题[2]。遗传算法是求解复杂的组合优化问题的有效方法。它将问题的可行解编码为由基因组成的染色体，通过模拟染色体群的选择、交叉和变异等操作，不断迭代，最终收敛到高适应度值的染色体，从而求得问题的最优解或满意解，非常适用于解决旅行商问题[3]。

二、问题提出

本文选取了上海市15个著名的旅游景点，旨在帮助同济大学嘉定校区的学生规划出合适的旅游路线。上海市交通便利，基本各景点都有地铁或公交可以到达，且班次较为固定，所以从学校到各景点以及各景点间往返所耗费的时间和路费基本固定，可以通过在上海公共交通平台查询，估计出各两点间行程的最短耗时。景点的最佳游览时长可根据以往经验估计出，为已知常量。如果游客到达景点时刻时的剩余时间不足以完整地游览景点，则选择当天不去此景点，而去另一景点或者返回出发点。

出于人身安全及拥有良好的游玩状态考虑，设定每天从学校出发时间为8点，晚上23点前必须返回学校。我们借助网络资源査阅了相关资料，确定了上海市15个著名的旅游景点，用自然数1，2，3……15为各个景点和地点编码；同时收集到了各景点的最佳游玩时间：

景点1:外滩，最佳游玩时间：4小时；景点2:豫园，最佳游玩时间：2小时；景点3:田子坊，最佳游玩时间：2.5小时；景点4:世博公园，最佳游玩时间：4小时；景点5:新天地，最佳游玩时间：1.5小时；景点6:复旦大学，最佳游玩时间：3小时；景点7:老城隍庙，最佳游玩时间：2.5小时；景点8:外白渡桥，最佳游玩时间：4小时；景点9:上海博物馆，最佳游玩时间：6小时；景点10:金茂大厦，最佳游玩时间：2小时；景点11:思南路，最佳游玩时间：2.5小时；景点12:静安寺，最佳游玩时间：1小时；景点13:1933老厂坊，最佳游玩时间：2小时；景点14:古漪园，最佳游玩时间：2小时，景点15:杜莎夫人蜡像馆，最佳游玩时间：3小时。

表1表示了各景点间的交通时间：

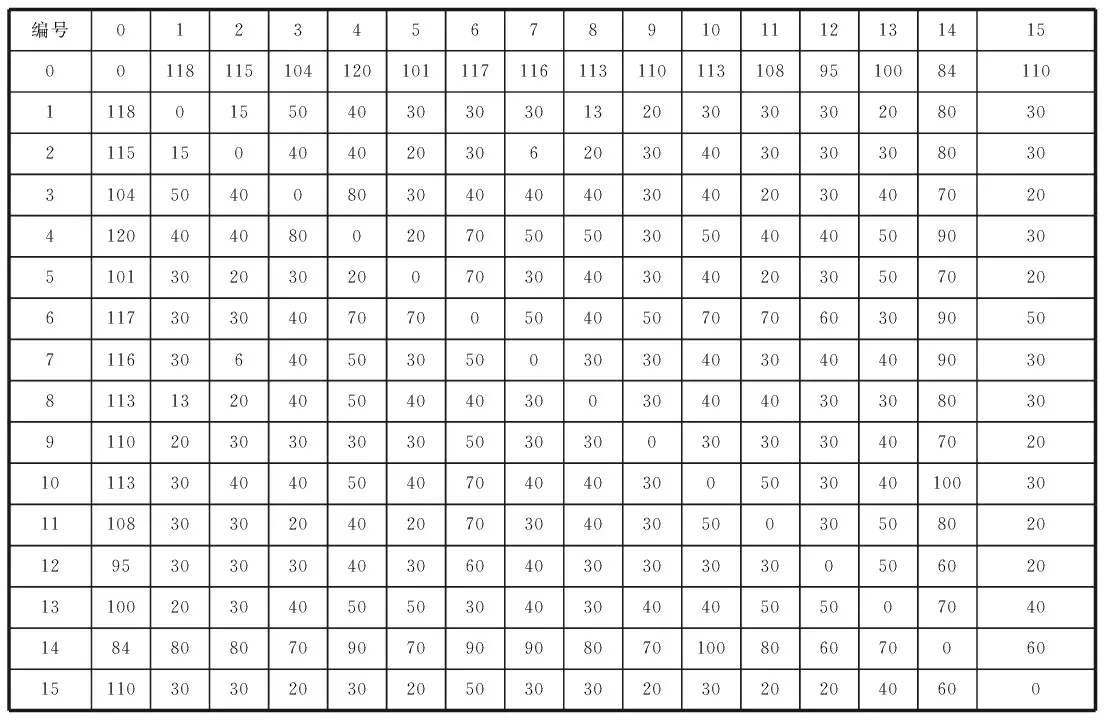
表1　各点间的交通时间(单位：小时)

三、模型假设与符号说明

(一)基本假设

(1)所有的公共交通都是准点出发，不存在故障或停运等突发性情况；

(2)旅游者每天都是八点准时从学校出发，在各景点逗留时间固定；

(3)对于道路的拥堵程度不予考虑，认为都是畅通的；

(4)天气等一切突发情况不考虑在内；

(5)每个旅游景点只游览一次。

(二)符号说明

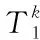
四、模型建立及求解

(一)目标函数的确立

由于游览完全部景点所花费的门票、购物等费用基本相同，唯一的区别在于交通费用，而往往走过的路程最短，相应的交通费往往也会更短，同时路程与时间一般也成正比，所以本模型的目标可以抽象为花费最少的时间游览完这15个景点，游览的总时间T包括了往来于各景点、学校间的时间，即总交通时间T1，以及在景点逗留游玩的总时间T2

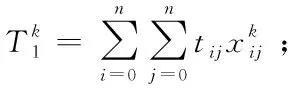
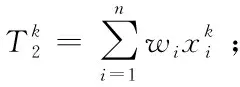
为简化运算，本文决定根据游客每天回到学校即出发点的时刻减去出发时刻，来得到该日的总游完时间。已知游客于每天早上8点从同济大学嘉定校区出发，假设第k天游玩返回学校的时刻是hk，则这天旅游所耗费的时间tk则为(hk-8)个小时，m天一共花费的旅游时间则为每天旅游时间之和，目标函数为：

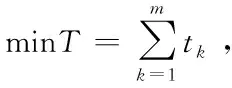
(二)约束条件

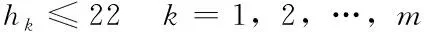
(三)基于遗传算法的模型求解

遗传算法在求解NP问题中得到了普遍运用，其包括初始化种群、评价种群中个体的适应度、选择运算、交叉运算、变异运算和终止判断等基本步骤，下面将对其原理进行阐述。

(1)编码

利用遗传算法求解问题不是直接作用于问题的解空间上，而是利用解的某种编码表示，而编码是指在遗传算法中如何描述问题的可行解，即把问题的可行解从解空间转换到遗传算法所能处理的搜索空间的转换方法。常用的遗传算法编码方法有：二进制编码、符号编码、树编码、自适应编码、乱序编码等[4]。本文将采用符号编码方法，其主要特点是意义明确，遗传操作不需要频繁地编码解码，计算复杂性降低，算法效率较高。

本文研究15个旅游景点的路径规划问题，每个景点用一个自然数表示，随机生成1～15的15个自然数的随机排列，便组成了一条染色体，如2 8 3 1 15 6 9 12 14 10 4 7 5 13 11。

(2)适应度函数设计

本文以时间最小化作为目标函数，且总取非负数，故可直接利用目标函数构造适应度函数，可表示为：F=tk

(3)算法参数设置

下面对GA的参数作出说明：

种群个数：70；迭代次数：150；交叉率：0.9；变异率：0.1；

(4)遗传操作

①种群初始化

随机产生含有70个个体的初始种群。

②个体评价

此步骤是对繁衍出来的后代进行评估打分。在本文研究的问题中，时间越少，分数越高。

③选择运算

选择的目的是为了从交换后的群体中选出优良的个体，使它们有机会作为父代为下一代繁殖子孙。选择以达尔文的适者生存为原则，适应性越强的个体为下一代贡献的概率也就越大。本文将适应度按照从小到大的顺序排列，选取前70个个体作为下一代进行繁殖。

④交叉运算

交叉运算是遗传法中产生新个体的主要操作过程，它以某一概率相互换某两个个体之间的部分染色体。本文采用单点交叉的方法，对于随机生成的70*16初始种群矩阵，先对种群随机配对，再随机设置交叉点位置，从而把母体对中两个个体从交叉点分为前后两段，确定交叉概率0.9，当产生的随机数小于交叉概率时，将两个个体的后半部分交换。如生成[1,15]内的随机整数r=9，对9之后的位置部分进行交叉。

283115691214104751311

491411361181572510312

交叉为：

28311569121572510312

4914113611814104751311

⑤变异运算

变异运算是对个体的某一个或某一些基因座上的基因值按较小的变异概率进行改变，它也是产生新个体的一种操作方法。如生成[1,15]内的随机整数r1=5和r2=8，将其代表的位置对换。

28311569121572510312

变异后：

28311269151572510312

(5)终止

本文以进化代数作为遗传算法的终止条件。可将经过150代遗传筛选出的最优基因，近似认为得到了最优解。当然，可以通过无限增加初始种群以及繁衍代数，得到理论上的最优解。本文求解迭代过程如下图2所示，最后函数值稳定在61.3左右。

图1　迭代逼近真值图

(四)结果分析

本文运用遗传算法求解了该旅游路线规划模型，通过MATLAB 2015b编程，得到了在有往返时间限制和起点终点固定的前提下，游览完这15个景点所用的最短时间为61.3h，共需要5天完成，同时得出了相应的5条旅游路线，各路线路径及到达各点的时刻等详情如下所示：

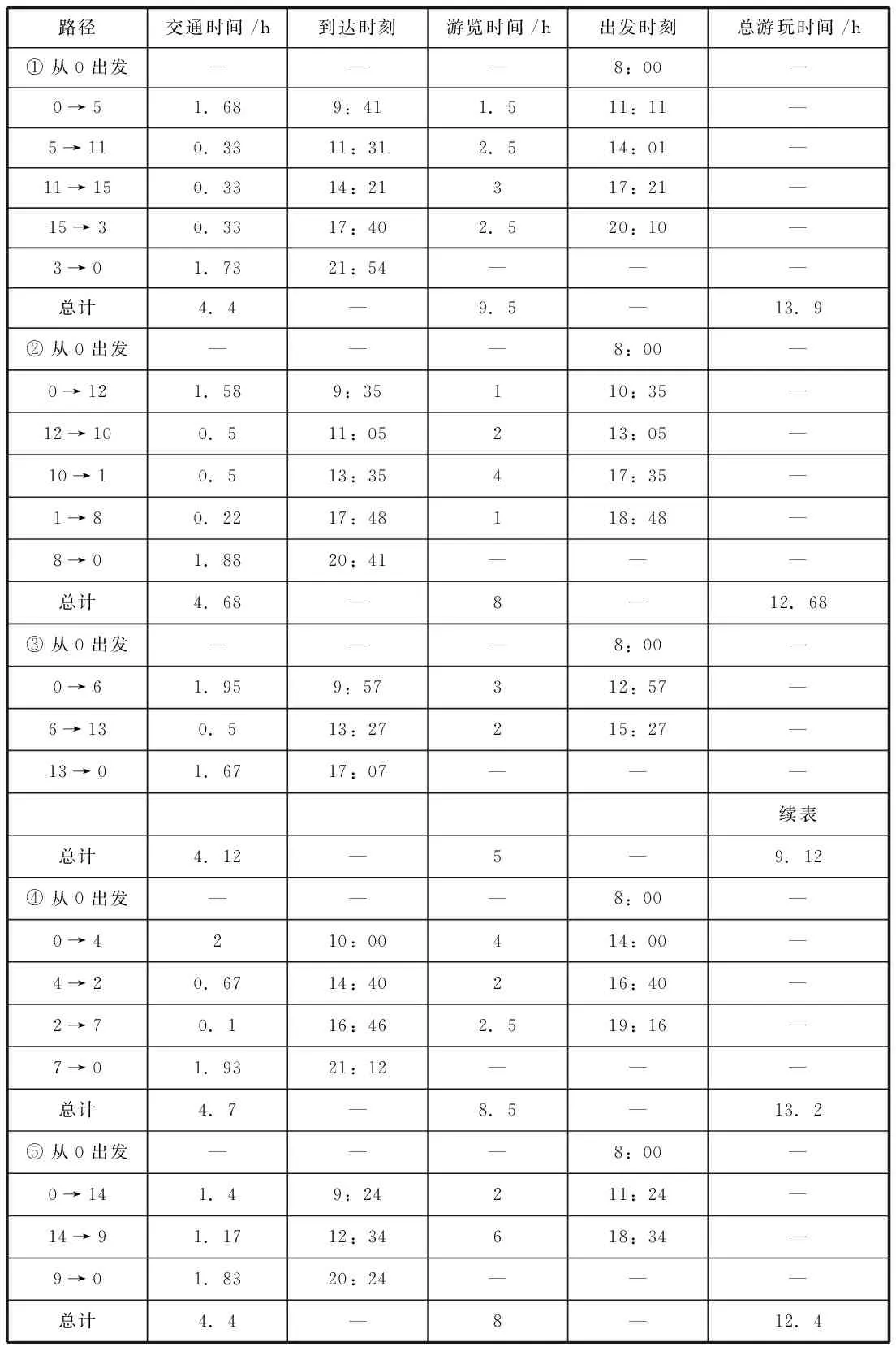
路径交通时间/h到达时刻游览时间/h出发时刻总游玩时间/h①从0出发———8:00—0→51.689:411.511:11—5→110.3311:312.514:01—11→150.3314:21317:21—15→30.3317:402.520:10—3→01.7321:54———总计4.4—9.5—13.9②从0出发———8:00—0→121.589:35110:35—12→100.511:05213:05—10→10.513:35417:35—1→80.2217:48118:48—8→01.8820:41———总计4.68—8—12.68③从0出发———8:00—0→61.959:57312:57—6→130.513:27215:27—13→01.6717:07———续表总计4.12—5—9.12④从0出发———8:00—0→4210:00414:00—4→20.6714:40216:40—2→70.116:462.519:16—7→01.9321:12———总计4.7—8.5—13.2⑤从0出发———8:00—0→141.49:24211:24—14→91.1712:34618:34—9→01.8320:24———总计4.4—8—12.4

五、模型的评价、改进及推广

本模型为身处同济大学嘉定校区的同学外出旅游提供了一定的参考，具有明确的现实意义。旅游者可根据自身实际情况，只需对旅游景点、游玩时间、出行时间等参数做出些许调整，即可带入模型，得出适宜的旅游路径，不仅有助于其有目的地选择并安排自己的旅游活动，避免漫无目的地游玩，而且还可以使其合理利用时间，争取游览更多的风景，并且合理的路径规划也增加了旅游者游玩的舒适度和愉悦感。

综上分析，本模型适用于有时间约束的定点往返的路线规划问题，具有广泛的使用意义。但是，本模型由于未将一些现实因素纳入考虑范围，还存在以下几点不足：

(1)实际情况中，多数景点都有规定的开放时间，本文只选取了开放时间较为宽松的旅游景点为例，在日后的研究中，可将景点的开放时间考虑其中，以期规划出更加贴合实际的旅游路线。

(2)景点游玩时间的长短往往因人而异，本文仅根据以往经验估计出了一个大概值，灵活性较差，可在日后对模型进行改进，增加游玩时间的弹性，将其设定在一个合理的区间内。

(3)现实生活中，人们在出行时往往会选择多种交通工具，并且选择的交通工具不同，所花费的交通时间自然也有所不同。另外，不同的时间路况信息有所差别，出行高峰期所花费的时间一般比低谷期长。本文仅选择了频次、时间相对固定的公共交通作为交通工具进行研究，未考虑不同交通工具、不同出发时间的影响。