基于灵敏度分析的系统运行可靠性薄弱环节识别的研究

潘波，余梦天

（贵州大学电气工程学院，贵州 贵阳 550025）

0　引言

对电力系统进行可靠性评估的一个重要目的就是发现系统的薄弱环节以便及时提出整改措施，有效预防某一元件或设备故障导致电网发生停电的事故[1]。虽然常规的可靠性指标能够反映整个电力系统以及各个节点的可靠性高低，但是，由于缺乏对其组成设备的具体分析，不能准确找到系统的薄弱环节[2-9]。因此，须找到一种可以有效识别出系统可靠性薄弱环节的方法，为改善系统可靠性参数、提高系统可靠性提供理论依据。

国内关于灵敏度分析的研究还处于起步阶段，目前，电力系统可靠性指标的灵敏度分析大多是通过可靠性指标对元件可靠性参数求一阶偏导数得出的，通过解析法计算灵敏度指标，该方法虽然可以找出系统的薄弱环节，但其中也存在着一些不足[10-15]。一方面，在计算方法上，常规的灵敏度计算主要是通过状态枚举来计算系统可靠性指标和可靠性指标对元件参数的灵敏度，该方法具有严格的指标计算公式，可以得到比较精确的计算结果，但现代电力系统规模不断扩大，涉及的元件数量很多，如果考虑所有故障状态，形成的状态数量巨大，计算时间十分长。另一方面，在可靠性指标和元件参数上，常规的灵敏度分析涉及的是系统年度化可靠性指标同时认为元件可靠性参数是固定不变的，而在系统实际运行过程中，元件参数会发生实时变化，常规灵敏度分析没有反映系统运行过程中的薄弱环节[16-19]；而且当多个参数发生变化或者参数变化幅度较大时，仅仅用一阶灵敏度求解的近似值在精度上很难满足要求，所以这就需要二阶灵敏度甚至高阶灵敏度来分析。

针对常规灵敏度分析的不足，本文在对系统运行可靠性薄弱环节进行研究中，采用系统短时可靠性指标和元件时变可靠性参数，例如故障率、修复率等都是随运行条件发生实时变化的变量，并且推导系统运行可靠性指标对元件时变参数的二阶灵敏度表达式，建立了系统运行可靠性二阶灵敏度计算模型，完善灵敏度分析方法。

1　运行可靠性指标对元件参数的一阶灵敏度分析

常规系统可靠性的灵敏度分析是求各指标分析函数的期望E(F)对元件参数的偏导，系统元件参数中元件故障率λk、元件修复率μk等都为常数。与常规灵敏度分析不同，本文研究运行可靠性薄弱环节，需要通过系统短时可靠性指标对元件时变参数求偏导数得到灵敏度计算模型，因此元件参数都是时变的，元件故障率λk、元件修复率μk等都为变量。

1.1　失负荷概率LOLP对元件参数的解析表达式和一阶灵敏度分析

1）LOLP对元件k的可靠性参数λk(t)和μk(t)的解析表达式如下:

式（1）～（3）是失负荷概率LOLP对元件可靠性参数λk(t)和μk(t)的解析表达式，H1，H2是两个重要的系数。在一个实际电力系统中，H1，H2是两个常数，因此，失负荷概率LOLP是以参数λk(t)和μk( t)为变量的函数表达式。H1表示元件k在任何时候都处于正常工作状态时由系统其它元件发生故障所引起的失负荷概率，即H2表示元件k在任何时候都处于故障状态时，由系统其它元件发生故障所引起的失负荷概率，即

2）LOLP的解析表达式和对元件k的可靠性参数的一阶灵敏度的表达式如下：

将式（1）对元件故障率、元件修复率、元件有效度以及元件无效度求一阶偏导数，可以得到LOLP对元件k的可靠性参数的一阶灵敏度其表达式如下所示。

1.2　失负荷频率LOLF对元件参数的解析表达式和一阶灵敏度分析

1）LOLF对元件k的可靠性参数λk(t)和μk(t)的解析表达式如下:

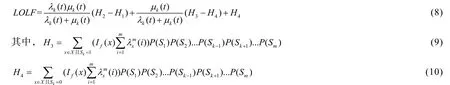
2）LOLF的解析表达式和对元件k的可靠性参数的一阶灵敏度表达式如下：

根据式（8）可以导出失负荷频率元件故障率λk(t)、元件修复率μk(t)的一阶灵敏度表达式，表达式如下所示：

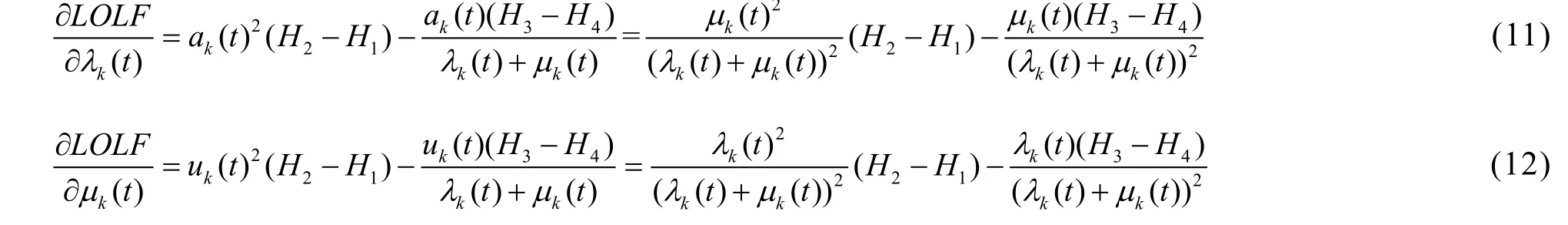
1.3　电力不足期望EDNS对元件参数的解析表达式和一阶灵敏度分析

1）EDNS对元件k的可靠性参数λk( t)和μk(t)的解析表达式如下:

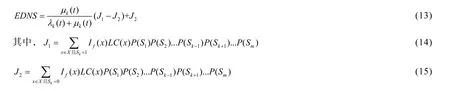
2）EDNS的解析表达式和对元件k的可靠性参数的一阶灵敏度表达式如下：

通过式（13）对元件时变参数求一阶偏导数，可以得到EDNS对元件k的可靠性参数的一阶灵敏度其表达式如下所示。

2　运行可靠性指标对元件参数的二阶灵敏度分析

2.1　失负荷概率LOLP对元件k的可靠性参数的二阶灵敏度分析

在式（5）～（7）的基础上推导了LOLP对元件可靠性参数的二阶灵敏度表达式。LOLP对元件故障率λk(t)和修复率μk(t)的二阶灵敏度表达式如下所示：

2.2　失负荷频率LOLF对元件false的可靠性参数的二阶灵敏度分析

在式（11）和式（12）的基础上推导LOLF对元件故障率λk(t)和修复率μk(t)的二阶灵敏度表达式：

2.3　电力不足期望EDNS对元件k的可靠性参数的二阶灵敏度分析

在式（17）～（19）的基础上推导EDNS对元件k的可靠性参数的二阶灵敏度表达式。EDNS对元件故障率λk(t)和修复率μk(t)的二阶灵敏度表达式如下所示：

3　算例分析

本文在计算IEEE-RTS79输变电系统短时失负荷概率LOLP、失负荷频率LOLF、电力不足期望EDNS等指标的基础上，分别计算元件故障率、元件修复率、元件有效度和元件无效度的一阶、二阶灵敏度，以找出其薄弱环节。以LOLP为例展开分析，IEEE-RTS79系统接线图如图1所示，按节点顺序对元件进行排序，序号1～32为发电机，序号33～37为变压器，序号38～70为输电线路。

3.1　系统可靠性指标元件可靠性参数的一阶灵敏度指标

从表1可以看到该输变电系统的总体可靠性指标，但是仅通过可靠性指标不能判断究竟是那些薄弱元件造成系统可靠性差的原因。本章介绍了通过可靠性指标对可靠性参数的灵敏度分析找出系统存在的薄弱环节。下面计算各个元件的灵敏度指标，将计算结果进行降序排列，筛选出排名前5的指标。一阶灵敏度指标如表2～4所示。

图1　IEEE-RTS79靠性测试系统接线图Fig.1 IEEE-RTS79 reliability test system wiring diagram

表1　IEEE-RTS79只考虑输变电系统的可靠性指标Table 1 IEEE-RTS79 only considers the reliability index of power transmission and transformation systems

表2　失负荷概率LOLP对元件可靠性参数的一阶灵敏度指标Table 2 First-order sensitivity index of the probability of loss of the reliability of components

表2列出了失负荷概率LOLP对元件可靠性参数的灵敏度指标，可以看到系统失负荷概率LOLP灵敏度指标排名前五的线路，这些线路对系统可靠性的影响较大，是系统的薄弱元件所在，对他们进行改善，可以有效的提高系统可靠性。

3.2　可靠性指标元件可靠性参数的二阶灵敏度指标

在上述一阶灵敏度分析的基础上，本节计算了各元件失负荷概率LOLP对元件可靠性参数的二阶灵敏度指标，同样对各元件灵敏指标降序排列后筛选出排名前5的元件进行分析，如表3所示。

表3　失负荷概率LOLP对元件可靠性参数的二阶灵敏度指标Table 3 Second-order sensitivity index of the probability of loss of the reliability of components

从表中可以看出，表3失负荷概率LOLP对元件时变可靠性参数的二阶灵敏度指标的元件排列顺序与一阶灵敏度指标排列顺序一致，这也验证了本文二阶灵敏度分析的准确性。

3.3　设元件参数变化后系统的灵敏度精度值对比

为了体现当元件可靠性发生变化时，一阶灵敏度和二阶灵敏度是否还能精确反映元件的灵敏度，本节取上述计算所得灵敏度指标排名前5的元件运行Δt小时后的可靠性参数重新计算其灵敏度指标，将参数变化前后灵敏度指标误差进行对比分析，以LOLP对元件可靠性参数的灵敏度指标为例，取Δt=10，计算结果如表4～8所示。

表4　参数变化后灵敏度指标精度对比Table 4 Comparison of parameter changes sensitivity index accuracy

由表4可以看到，随着系统运行Δt小时后，元件故障率λk(t)产生变化，各元件的一阶灵敏度和二阶灵敏度也随之发生变化，将参数变化前后的灵敏度指标误差进行对比可以看到，一阶灵敏度的误差高于二阶灵敏度。一阶灵敏度的误差很大，远高于二阶灵敏度计算的误差，所以元件参数变化的情况下，二阶灵敏度可以减少了元件薄弱环节识别的误差。这也证明了本文二阶灵敏度分析在元件参数变化的情况下仍然可以维持较高的精度。

3.4　计及不同运行方式的系统运行可靠性分析

系统在运行过程中运行方式可能会发生变化，当系统不同线路停运时，系统网架结构会发生变化，此时系统的可靠性指标以及灵敏度指标都会发生变化，因此本文对计及不同运行方式的系统运行可靠性进行分析。假设系统有以下两种运行方式：

1)方式一：线路38、线路42、线路48停运;

2)方式二：线路39、线路41、线路45停运。

两种不同方式的系统可靠性指标结果如表5所示，灵敏度分析以LOLP对元件可靠性参数的二阶灵敏度指标为例，结果如表6和表7所示。

表5　计及不同运行方式的系统可靠性指标Table 5 System reliability index under different operating modes

表6　输变电系统二阶灵敏度指标(方案一 )Table 6 Second-order sensitive index of power transmission and transformation system of the first option

表7　输变电系统二阶灵敏度指标（方案二 ）Table 7 Second-order sensitive index of power transmission and transformation system of the second option

在表5～7中可以看到在运行方式改变后，系统的运行可靠性指标和灵敏度指标都发生了变化。从表6中可以看到，灵敏度最大的前三条线路为线路46、47、43，因此这三条线路也是该运行方式下系统较薄弱的环节。从系统接线图来看，当线路38、42、48停运时，线路46为节点4和节点9之间唯一的连接线路，一旦线路46发生故障，节点4就会与系统发生解列；线路47是节点5和节点16之间唯一的线路，一旦线路47发生故障，节点16就会与系统发生解列。从表7可以看到，当线路39、41、46停运时，线路44、47、49这三条线路成为了该运行方式下系统较薄弱的环节。从系统接线图来看，这三条线路停运时，线路44成为节点2和节点6之间唯一连接的线路，一旦线路44发生故障，节点2会与系统发生解列；线路49成为节点4和节点15之间唯一连接的线路，当线路46发生故障时，节点4与系统发生解列。综上可以见得，当系统处于不同运行方式时，系统的运行可靠性指标及系统薄弱环节都会发生变化，因此研究计及不同运行方式的运行可靠性十分必要。

4　结论

本文主要对输变电系统运行可靠性灵敏度进行分析，并识别系统运行过程中的薄弱环节。首先，在现有文献基础上推导了系统运行可靠性指标（如失负荷概率LOLP、失负荷频率LOLF、电力不足期望EDNS）对元件时变可靠性参数（元件故障率、元件修复率、元件有效度和元件无效度）的二阶灵敏度计算公式，并对其重要系数进行了详细的解释。其次，以IEEE-RTS79系统作为算例，计算并对比了一阶和二阶灵敏度指标，验证了本文二阶灵敏度分析的可行性。然后，计算了元件参数发生变化后的二阶灵敏度指标，验证了本文二阶灵敏度分析精度更高。最后，计算了不同运行方式下的系统二阶灵敏度指标，验证了本文二阶灵敏度分析可以识别系统运行过程中的薄弱环节。综上，本文为运行可靠性分析提供了一种可行、有效的薄弱环节识别方法。