基于改进FUKF的燃气轮机性能退化诊断

曾　力,　龙　伟,　李炎炎

(1. 四川大学空天科学与工程学院, 四川 成都 610065; 2. 四川大学制造科学与工程学院, 四川 成都 610065)

燃气轮机气路主要由进气道、导流叶片、压气机、燃烧室、涡轮等组成,这些部件在工作期间,受到高温、高压、高应力、吸入物、粉尘等的影响,性能不断退化甚至出现部件的突发性失效,导致灾难性后果[1-3].因此,如何对气路部件的工作状态进行监控,评估燃气轮机的健康状况,为发动机维修提供合理的依据是当前研究的一个重点.通常健康状况可用健康参数表示,例如风扇、高低压压气机的效率系数和流量系数等,这些参数不可或难以直接测量.由于健康状况的变化可以通过一些可测量参数(高低压转子转速,压气机进气口压力、温度,燃烧室进气压力、温度等)的变化得以体现.因此,可以通过传感器获取这些可测量参数,建立这些参数到系统健康参数的映射模型,然后利用估计算法推导相应的健康参数.

无迹卡尔曼滤波器(unscented Kalman filter, UKF)是以卡尔曼滤波器作为框架,通过无迹变换(unscented transformation, UT)来逼近非线性函数的样本和均值,没有忽略高阶项.UKF是对分布的概率密度函数的近似,避免求解Jacobian矩阵,其精度要高于扩展卡尔曼滤波器(extended Kalman filter, EKF).目前,UKF已应用于燃气轮机气路部件故障问题的诊断.Sebastien等[4]提出一种基于卡尔曼滤波与主成分分析的混合算法,通过把测量数据分解到主元空间和残差空间,在两个空间中分别构造两个统计量,结合卡尔曼滤波实现对燃气轮机性能的监测与故障诊断.张鹏[5]针对计算误差与噪声引起的协方差矩阵负定的问题提出根据残差的变化来改进滤波收敛速度的办法.李冬等[6]提出通过主元分析对测量参数进行分解,提取反映性能衰减的成分,据此建立卡尔曼滤波模型.胡宇等[7]针对发动机气路故障诊断模型建模不准确的情况,提出采用高斯回归过程(Gauss process regression, GPR)对训练数据进行建模,利用超球体单行采样和平方根滤波来提高滤波的稳定性.

燃气轮机在工作中,随着使用周期的增加导致的气路部件老化或是突发性状况,可能出现状态突变的情况[8-9].这种情况下,普通的UKF无法根据测量值的变化准确估计出健康参数.针对这个问题,本文提出基于残差相似性的渐消无迹卡尔曼滤波法(fading unscented Kalman filter based on residual similarity, FUKF-RS),通过强制残差序列保持正交来确定渐消因子.针对遗忘因子ρ通过经验值获取而导致影响估值精度的问题,利用残差阵的相似度代替遗忘因子计算误差阵.另外,在构造滤波器时采用最小偏度采样.此时采样点个数为n+2(n为状态空间维数),小于对称采样的样本点数2n+1,缩短了运算时间.实验证明此方案能够在确保精度的情况下,增加系统的鲁棒性,加强对突变状态的跟踪能力,其计算复杂度较低.

1　发动机健康参数估计算法设计

1.1　对突变状态的估计

UKF算法将卡尔曼滤波的使用条件从线性场合推广到非线性场合,并具有较高的估计精度.但是对于一些强非线性场合,例如被估计对象的状态发生大范围突变的时候,UKF的估值精度会发生大幅度下降.图1描述某型燃气轮机的高压涡轮在不同时刻发生跳变时,利用UKF对涡轮流量系数进行估计得到的曲线.

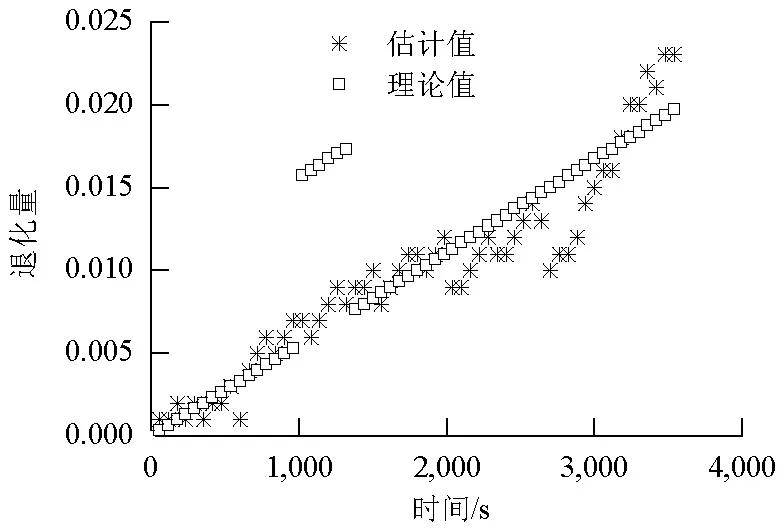
图1　基于UKF的流量系数突变时的估计值Fig.1　Estimation of the discharge coefficientduring state mutation based on UKF

图1中,在第1 000 s和1 450 s时,高压涡轮的状态发生了突变,导致流量系数发生了2次跳变,但UKF的滤波曲线较为平滑,与真实值相比,无法准确跟踪其值的变化.造成这种情况的主要原因是状态的突变导致量测值残差突然变化,而由于滤波器中当前数据所占比重较小,使得残差变化值引起的滤波增益不够大,无法通过估计值来体现出状态的突变.利用渐消卡尔曼滤波(fading unscented Kalman filter, FUKF)算法可以提高滤波器对参数突变的跟踪能力,其思想是给预测协方差乘以一个加权因子,通过改变加权因子的大小来调节历史数据和当前数据所占的比重来达到跟踪突变状态的作用.将其应用在燃气轮机气路部件故障诊断分析中,利用滤波器由系统的测量参数估计出健康参数.

1.2　估值算法的设计

本文对健康参数的估计采用FUKF,结合燃气轮机的结构点,算法如下[10]:

(1) 采集样本点并确定其相应的权值

根据前面所述,按照最小偏度采样的办法采集样本点,并计算其相应的权值,具体计算公式参见文献[11].时刻k健康参数为χi,k,其中,i=1,2,…,10,代表第i个样本.χi,k由高压涡轮(h)、低压涡轮(l)、风扇(f)、高压压气机(p)的效率系数(下标e)和流量系数(下标d)组成,即χi,k=(he,hd,le,ld,fe,fd,pe,pd)T.

(2) 健康参数一步预测

基于燃气轮机模型实现健康参数的一步预测,第i列健康参数在时刻k+1的预测值为

(1)

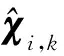
wk为燃气轮机的系统噪声.

(3) 健康参数均值和方差的计算

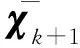
(2)

(3)

(4) 测量参数一步预测

基于燃气轮机模型实现测量参数的一步预测,第i列测量参数在时刻k+1的预测值为

(4)

式中:f(·)为发动机的非线性测量模型;

vk为测量系统的噪声.

(5) 测量参数均值和方差的计算

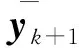
(5)

(6)

式中:Gk+1=diag (r1,(k+1),r2,(k+1),…,r8,(k+1))为渐消阵;

rg,(k+1)为第g个渐消因子,其值用于调节第g个测量参数的方差(g=1,2,…,8).

(6) 健康参数与测量参数间协方差的计算

时刻k+1健康参数与测量参数之间的协方差为

(7)

(7) 健康参数修正

健康参数修正主要包括时刻k+1卡尔曼增益Mk+1计算(如式(8))、健康参数估计值χk+1的修正以及协方差Pk+1的更新.

(8)

修正后的健康参数最优估计值为

(9)

式中:yi,k+1为时刻k+1的传感器实时测量值;

χk+1为健康参数一步预测值.

时刻k+1健康参数协方差阵修正值为

(10)

1.3　渐消因子求解

使FUKF稳定工作的条件是在确定卡尔曼增益Mk+1时,满足时刻k及时刻j测量参数残差之间的协方差为0[9]，即

(11)

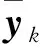
定义时刻k、j测量参数残差的协方差为

(Pχy,k-Mk+1Ck),

(12)

式中：ψ(·)为健康参数最优估计值随采样时刻的变化函数;

Pχy,k为时刻k的健康参数与测量参数之间的协方差；

Ck为时刻k测量参数残差的方差.

通过式(11)强制每一步残差序列保持正交可以确保序列中的信息全部被提取出来用于当前状态估计,同时滤波器具有自适应跟踪状态变化的能力.当滤波器保持稳定输出时,此时增益最优,Ckj=0;如果系统模型误差较大时,Ckj≠0,增益值并非最优,此时可通过调节渐消因子Gk+1使等式Pχy,k-Mk+1Ck=0成立,那么可认为增益最优,此时

(13)

式中:I为对角元素为1,其余元素为0的单位矩阵.

利用先验知识可以确定渐消因子之间的比值为

r1,(k+1)∶r2,(k+1)∶…∶r8,(k+1)=a1∶a2∶…∶a8,

(14)

式中：ag为渐消因子的比值.

令ag=vgck+1，其中ck+1为比例公共因子.

根据前面描述的渐消无迹卡尔曼滤波器成立的条件及渐消阵Gk+1可得

Ck+1=ck+1diag (a1,a2,…,a8)×

(15)

式中:Rk+1为测量噪声方差.

对式(15)两边求迹,整理可得

(16)

式中：tr(·)为矩阵求迹运算符.

从式(17)可得单个渐消因子的求解公式.

(17)

残差阵由前后时刻残差值按不同比例组成,如式(18)所示.

(18)

可以通过先验知识确定出a1,a2,a3,…,a8之间的比值，计算出因子ck+1便可以得到渐消因子的值.ρ值越大,越能突出当前残差的影响,ρ值越小,越突出历史信息的影响.ρ的取值通常是通过人为经验确定的,并没有精确的量化取值办法,过大或过小都会对状态估计结果造成影响.另外,根据滤波器为残差约束充分条件知道,基于残差约束的卡尔曼滤波器的渐消因子必须保证前后残差正交.如果系统状态发生突变,则残差阵将发生波动,无法确保正交.因此，本文提出利用前后估值时刻的残差阵的对角元素来构造向量，通过前后时刻向量的相似度来表征残差阵之间的相似性，并用该相似度值来替代ρ.

2　基于残差相似性的误差阵求解

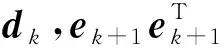
λt=dk,vk+1/(|dk|·|vk+1|).

(19)

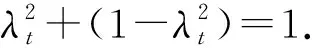
根据突出当前信息,兼顾历史数据的原则,Ck+1改为

(20)

式(20)确保了当前信息前的系数始终大于历史数据的系数.

3　实验仿真

针对某型航空燃气轮机气路部件性能渐变性退化和突变性退化,通过改变燃气轮机健康参数的值来模拟实际工作中出现的故障.通过渐变和突变的方式,改变健康参数,从而达到模拟部件性能退化的目的,分别利用FUKF和FUKF-RS对健康参数进行估计,通过变化量的形式对健康参数的退化值进行表示.另外,为了与图1对比,分别利用FUKF和FUKF-RS对图1条件下的状态突变进行估计.

仿真环境为高度H=0,马赫数为0,分别施加系统噪声Q和测量噪声R,分别为0. 0022In×n和0. 0022Im×m.在初始时刻，样本点取值均为1，即he=hd=Le=Ld=fe=fd=Pe=Pd=1.设定整体仿真计算时间为3 600 s,每隔60 s采集一次传感器的测量值,同时估计此时对应的健康参数值.仿真中根据故障原理设定风扇、压气机的效率系数和流量系数均下降,高、低压涡轮的效率系数下降,流量系数升高.其中,fe、fd分别下降3%和3.5%,pe、pd分别下降2.5%和3%,he、he分别下降3%和4%,hd、ld均上升2%.本文只列出高压压气机的效率系数pe与流量系数pd的估计值，利用FUKF和FUKF-RS对pe与pd估值分别如图2、3所示.

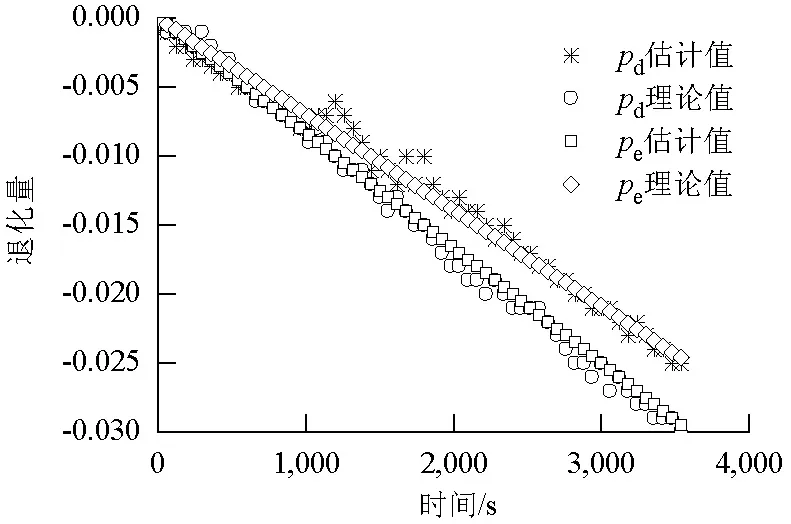
图3　基于FUKF-RS估计高压压气机的健康参数Fig.3　Estimation of the health parameter of high pressure compressor based on FUKF-RS

由图2可以看出，FUKF能估计出高压压气机健康参数的变化趋势,但与理论值相比,存在较大的误差,这是由于遗忘因子的取值不佳造成的.

相比图2、3的估值更接近于理论值.这是由于FUKF-RS使当前采样时刻测量参数残差的信息在进行测量值协方差更新过程中所占比例较大,更为接近实际测量工况.

针对图1中高压涡轮流量系数突变时估值不准的问题，分别利用FUKF和FUKF-RS对该工况下的流量系数估值，如图4、5所示.

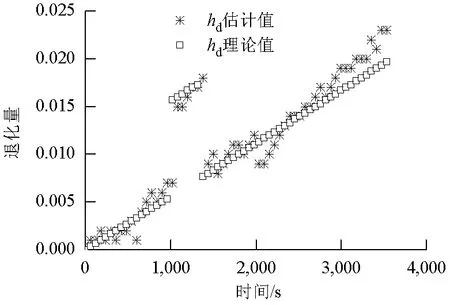
图4　基于FUKF-RS的高压涡轮流量系数突变时的估计值Fig.4　Estimation of the discharge coefficient of high pressure turbine during state mutation based on FUKF-RS

由图4可以看出,FUKF-RS具有较强的状态突变跟踪能力,相比图1的结果有了较大的提高.

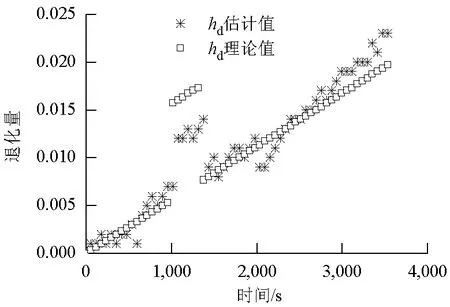
图5　基于FUKF的高压涡轮流量系数突变时的估计值Fig.5　Estimation of the discharge coefficient of high pressure turbine during state mutation based on FUKF

由图5可以看出,FUKF同样具有一定的突变跟踪能力,但相比FUKF-RS,其跟踪能力较低.

稳态时，FUKF-RS的状态估计精度较高，状态突变时，有较强的状态跟踪能力.主要是因为通过强制每一步估计的残差正交,确保残差序列中的信息被完全提取出来，这样使得滤波器具有对状态突变的跟踪能力.同时，利用表征残差相似性的参数来替代渐消算法中的ρ，避免了因为ρ取值不当造成的估值误差.

4　结　论

针对燃气轮机在长期工作过程中由于不断退化导致部件性能突变,引起健康参数在极短时间内出现突变,导致难以准确估计健康参数值的问题.

(1) 本文采用FUKF对健康参数估计,针对FUKF中求解渐消因子时存在的遗忘因子取值不当可能影响健康参数的估值精度的问题,提出FUKF-RS算法.

(2) 利用采样前后时刻测量值协方差矩阵的对角元素所组成向量的余弦值来表征向量之间的相似度,利用该相似度替代遗忘因子,实现了求解过程中的量化取值.

(3) 针对发动机部件出现故障,健康参数出现较大范围波动时,FUKF-RS相比FUKF,其参数跟踪精度提高了3%左右.而UKF则无法对健康参数进行准确估计.

(4) 发动机在正常工作,健康参数缓慢退化的情况下,FUKF-RS的估值精度相比FUKF提高了2%左右,且估值曲线更平滑.

致谢:四川大学实验技术立项项目资助(20170135).