基于卡尔曼滤波的快时变稀疏信道估计新技术
2018-07-12袁伟娜王嘉璇
袁伟娜, 王嘉璇
(华东理工大学信息科学与工程学院, 上海 200237)
OFDM (orthogonal frequency division multiple-xing)技术具有高频谱利用率和抗多径干扰能力,目前在3GPP(3rd generation partnership project)、4G LTE (long term evolution)等多种无线通信标准中得到了广泛应用.随着无线通信技术的发展,人们对许多从前未被重视的应用场景下的通信质量需求提高,比如:信道具有稀疏特性的偏远空旷的郊外山区,或信道具有快速变化的高速铁路等场景.信道估计的性能是衡量通信系统性能的主要标准,因此对于复杂多样化信道估计技术的研究具有重要的意义[1-3].
在郊区山区等呈现稀疏特性的信道环境下,信道多径时延分布是零散的,即由几个具有明显响应的主径,以及大部分低于一定阈值近似为0的径组成.如果仍假设主径连续集中在前几径,误差将大大增加,而如果对最大时延内所有径数进行估计,估计数量也将增加.压缩感知(compress sensing, CS)的提出对稀疏信道估计问题提供了很大的帮助,文献[4-6]基于CS算法分别研究了单天线和多天线OFDM系统时不变稀疏信道估计,文献[7-9]基于CS算法和传统估计算法研究了时变稀疏信道估计,文献[10]采用卡尔曼滤波算法(Kalman filter, KF)与CS相结合的算法研究慢时变稀疏信道估计,此处的慢时变指单个符号内信道响应不变而相邻符号间是变化的,该算法不适合用于快时变信道的估计.
在高铁等信道环境中,由于多普勒效应的存在,信道在一个符号周期内快速变化,称其为快时变信道,此时,待估计的信道参数数量大大增加.文献[11-12]采用基扩展模型(basic expansion model, BEM)对每一个OFDM符号块对应的快时变信道建模,该模型可以对快时变信道特性进行较好的拟合,同时也可以降低估计参数数量,然后采用LS(least square)、 LMMSE(linear minimum mean square error)和ML(maximum likelihood)对BEM系数进行估计,没有考虑相邻符号块间信道参数的关系.文献[13]考虑了相邻符号块信道参数的关系,采用KF算法对相邻符号对应的BEM信道模型系数进行估计,从而获得信道估计,但研究的是非稀疏信道,将该算法应用于稀疏信道估计时,性能较差.目前,尚未查阅到考虑相邻符号块间信道参数关系的快时变且稀疏的信道估计算法.
本文提出一种新的快时变稀疏信道估计方法.该方法基于快时变稀疏信道的BEM模型,采用CS算法进行主径估计,再结合KF算法估计BEM系数,进而获得信道估计值.同时,实验仿真表明,本文提出的方法有效地减小了信道估计的误差.
1 基于BEM的快时变信道模型
OFDM系统的时域接收信号模型为
(1)
式中:x、y分别为发送与接收的OFDM符号;
h(n,l)为一个OFDM符号周期内第l径第n个采样点的信道响应;
N为一个符号周期总采样点数;
(·)N表示模为N的循环移位;
L为最大时延内总径数;
w(n)是第n个采样点的均值为0、方差为σ2的加性高斯白噪.
BEM采用一组基函数的线性组合,可以较好地拟合快时变信道的信道响应,表示如式(2).
(2)
式中:n=0,1,…,N-1;
l=0,1,…,L-1;
bq(n)、gq(l)和Q分别为BEM的基函数、系数和阶数.
通常假定在一个OFDM符号内,BEM系数保持不变,而基函数是一组固定的正交基,因此采用BEM可以将待估计的信道参数由NL个降到(Q+1)L个,大大减少了估计数量.得到BEM系数估计值后,再经过BEM模型即可获得信道响应.
常用的BEM基函数有:复指数基扩展模型(complex exponential BEM, CE-BEM)、过采样复指数基扩展模型(generalized complex exponential BEM, GCE-BEM)、多项式基扩展模型(polynomial BEM, P-BEM)、离散卡-洛基扩展模型(discreteKarhuen-loève BEM, DKL-BEM)和离散椭圆基扩展模型(discrete prolate spheroidal BEM, DPS-BEM).
式(2)写成矩阵形式为
(3)
式中:bq=(bq(0),bq(1),…,bq(N-1))T;
Gq为N×N维的Toeplitz循环矩阵;
h为N×N维的时域信道矩阵.
Gq和h表示如式(4)~(5).
(4)

(5)
式(1)写成矩阵形式为
y=hx+w,
(6)
式中:y=(y(0),y(1),…,y(N-1))T;
x=(x(0),x(1),…,x(N-1))T;
w=(w(0),w(1),…,w(N-1))T.
则相应的频域接收信号为
Y=FhFHX+W=HX+W,
(7)
式中:Y=Fy;
X为OFDM符号,
X=(FH)-1x;
F为N点傅里叶变换矩阵,
F=(Fij),i,j=0,1,…,N-1,
H为一个N×N大小的频域信道矩阵;
W为频域的噪声.
将式(3)代入后可表示为
Y=FhFHX+W=
(8)

gq=(gq(0),gq(1),…,gq(L-1))T.
令A=Fdiag(bq)FH,式(8)可以表示为
(9)

Y=AΔg+W,
(10)
再令S=AΔ,则频域接收信号最终可表示为
Y=Sg+W.
(11)
基于梳状导频辅助的估计方法,式(7)中导频处的接收信号可表示为
YP=SPgP+Sdgd+WP,
(12)
式中:WP为导频处的噪声;
SPgP为有效接收数据,p=1,2,…,P,P∈N;
Sdgd为数据子载波对导频子载波的干扰,令d=Sdgd,则有
YP=SPgP+d+WP.
(13)
2 基于压缩感知的稀疏信道时延估计
在稀疏信道的环境下,不需要完整地估计最大时延内所有径数的增益,只需对有明显增益的主要时延处Ldelay径进行估计.因此,要在信道增益估计前先在L中找出主径的位置Ldelay.
压缩感知理论的提出,给处理稀疏信号提供了一种思路.压缩感知是一种在稀疏条件下寻找欠定线性系统解的算法,可以用低于奈奎斯特采样频率去高度重建信号.对于一个未知的信号X∈CN,X中只有K个非零元素(K≪N),即信号X的稀疏度为K.选择一个观测矩阵Φ∈CM×N对X进行测量,观测过程表示为
Y=ΦX+V,
(14)
式中:V为噪声.
得到观测信号Y∈CM,其中M 正交匹配追踪(orthogonal matching pursuit, OMP)[14]算法是一种常见的基于贪婪迭代的压缩感知重构算法,其基本思想是初始化残差跟原始索引集,每次迭代通过计算内积,不断地找到与残差相关度最高的原子,并更新索引集,最后逐步逼近系数向量.利用OMP进行时延估计的过程如下: 步骤1初始化索引集T0=∅. 步骤2计算 式中:φt为Φ中的列; Γλ为Φ中所有列数. 步骤3更新索引集 Tn={Tn-1,φt}, LS估计 步骤4计算残差 rn=Y-TnXn, 并更新 步骤5重复步骤3、4,直到残差小于阈值或Tn的列数达到设定值K. 为了在稀疏信道估计中应用上述理论,需要构建稀疏信号和观测矩阵.假设发送端的所有导频信号为XP,则对应位置的接收端信号YP表示为 YP=HPXP+WP, (15) 式中:XP、YP均为NP×1维向量; WP为NP×1维导频处噪声; HP为NP×NP维频域信道响应,其对角元素为第p个导频位置处的频响,表示为 (16) 又由于导频处的多径信道频响表示为 (17) Pp为第p个导频在子载波中对应的位置. 在快时变环境下,每径信道响应在1个符号周期内每个采样点处都不同,但其平均值也可以表示总体的稀疏性.则可将1个符号周期内所有导频符号处对应的频响表示为 (18) 式中:HP=(H0,H1,…,HNP-1)T; Φ=(Φpl), 建立好上述快时变稀疏信道模型后,可应用信道估计算法对BEM系数g进行估计.传统的信道估计算法通常为LS和LMMSE. (19) 则可解得g的LS估计值为 (20) LS算法不需要信道和噪声的统计信息,因而复杂度较低.但同时也限制了性能的进一步提升,在干扰比较大或是信噪比较差的时候,信道估计的性能可能不够理想. (21) 则可解得LMMSE估计值为 (22) 式中:Rg、Rd和RW分别为BEM系数、发送数据和噪声的自相关矩阵. LMMSE算法考虑了噪声和信道的统计信息,因此性能优于LS.但同时复杂度也较高,而且要获取信道的统计信息也非常困难,如果得到的统计信息和实际信道不匹配,将会带来较大的误差.通常采用特定的信道,如本文采用的是Jakes模型信道[15],以方便计算信道的统计信息. 上述方法(LS或LMMSE)均是在对每一个OFDM符号块对应的信道参数分别进行BEM建模的基础上进行估计的,相邻符号块的参数之间并无相关.然而,在实际情况中,相邻OFDM符号之间对应的信道参数是随时间平滑渐进变化的[13].因此,考虑到这种情况,可以用自回归(autoregression, AR)模型[16]来描述和刻画相邻符号间对应的信道增益的这种动态变化,为了降低复杂度,这里选用一阶AR模型,如式(23). hml=Ahlh(m-1)l+uml, (23) 式中:hml为第m个OFDM符号第l径的信道响应向量; Ahl为信道系数的状态转移矩阵; uml为模型误差,是协方差为Ul的复高斯向量. 由于hml的BEM模型可写作 hml=Bgml, (24) 式中:hml=(hm(0,l),hm(1,l),…,hm(N-1,l))T; gml=(g0(l),g1(l),…,gQ(l))T; B=(b0,b1,…,bQ)为BEM基函数矩阵. 所以,经过BEM模型转换后的基系数可建立相似的AR模型,如式(25). gml=Aglg(m-1)l+uml, (25) 式中:Agl为BEM基系数的状态转移矩阵. AR模型参数可通过尤尔-沃克(Yule-Walker)方程解得 (26) 因为BEM系数是零均值的相关复高斯变量,其相关矩阵为 (27) 式中:s为相关移位的大小. 又由于本文采用的是Jakes模型信道[15],则 (28) fmax为最大多普勒频移; Ts采样周期; Ns=N+NCP为添加了CP的OFDM符号采样点数,NCP为循环前缀的长度; J0(·)为第1类零阶Bessel函数. 将各径的AR模型结合表示为 gm=Aggm-1+um, (29) Ag=diag{Ag0,Ag1,…,Ag(L-1}为L(Q+1)×L(Q+1)的状态转移矩阵; 在本文中,将式(29)看作KF算法的状态方程,将第m个符号对应频域接收信号看作KF测量方程,表示如式(30). (30) 采用KF算法估计多个OFDM符号对应的BEM系数[13],具体步骤如下所示: 步骤1初始化 g0=0L(Q+1)×1, P0=Rg(0), Rg(s)=diag{Rg0(s),Rg1(s),…,Rg(L-1)(s)}. 步骤2时间更新方程 gm|m-1=Aggm-1, 步骤3测量更新方程 gm=gm|m-1+Km(Ym-Smgm|m-1), Pm=Pm|m-1-KmSmPm|m-1. 上述步骤中:gm|m-1、gm、Pm和Pm|m-1分别为第m个符号的参数预测值、参数估计值、估计误差协方差矩阵和预测估计误差协方差矩阵; IN为N阶单位方阵. 通过Matlab仿真结果对算法性能进行验证.仿真参数参考文献[17]设置,如表1所示,仿真中采用QPSK (quadrature phase shift keying)调制,梳状导频,瑞利多径信道模型,GCE-BEM(Q=2).参考指标归一化多普勒频移表示为 (31) 式中:v为移动速度; c为光速; fc为载波频率. 表1 仿真参数表Tab.1 Simulation parameters 图1为信噪比(SNR)为20 dB时,随着fnd逐渐增大(fnd=0.1,0.2,0.3分别对应于速度v=150,300,450 km/h),各方法的信道估计NMSE(normalized MSE).其中,KF曲线对应于未采用CS时延估计(即认为主径连续集中在前5径且只估计前5径)[13]时的估计误差,其他3条曲线分别对应于采用OMP与LS、LMMSE和KF 3种方法的结合. 图2为fnd=0.2时,随着信噪比SNR增加,各方法的信道估计NMSE. 图1 SNR为20 dB,fnd增大时,各方法的NMSE对比Fig.1 NMSE vs. fnd for SNR is 20 dB 图2 fnd=0.2,SNR增大时,各方法的NMSE对比Fig.2 NMSE vs. SNR for fnd=0.2 图1和图2中:OMP-KF (orthogonal matching pursuit-KF)曲线为本文算法;OMP-LS和OMP-LMMSE曲线分别为将OMP与LS和LMMSE相结合的算法,这两种算法未考虑相邻符号块信道参数的变化关系;KF曲线为文献[13]中算法. 从图1中可以看出,fnd增大时各方法的估计误差都有所增加.其中,OMP-KF算法与只使用KF相比,由于应用了OMP进行稀疏信道环境下的时延估计,故误差远低于直接使用KF[13]的算法;而同时进行了时延估计的情况下,OMP-LMMSE算法考虑了噪声和信道的统计信息,因此误差低于OMP-LS,而OMP-KF算法由于考虑了相邻符号之间的平滑关系,其误差更低于OMP-LMMSE. 从图2中可以看出,与图1趋势相同,进行了时延估计的OMP-KF算法误差低于直接使用KF[13]的算法;而同样进行了时延估计时,在SNR较低时,OMP-KF算法的NMSE低于OMP-LS和OMP-LMMSE,SNR增加时,OMP-KF算法优势也增大,在SNR达到20 dB以后,误差变化趋于平缓. 针对快时变稀疏环境下OFDM系统的信道估计问题,本文基于快时变信道的BEM模型,采用压缩感知算法进行稀疏环境的时延估计,再采用卡尔曼滤波对BEM系数进行估计,从而得到信道增益.由于该算法综合考虑了快时变、稀疏信道以及连续符号间的信道参数的平滑特性,相对于只考虑慢时变或非稀疏信道的算法,一定程度上提升了信道估计性能,最后通过仿真实验进行了验证.

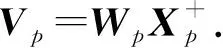


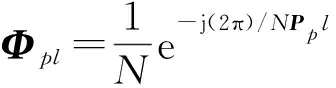
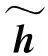
3 基于卡尔曼滤波的信道估计
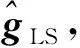
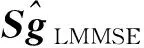

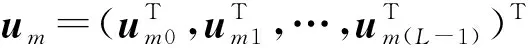
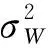
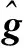
4 实验仿真



5 结束语
