脉冲干扰复数域Cohen-Grossberg神经网络的稳定性
2018-07-12徐晓惠施继忠张继业陈子龙
徐晓惠, 徐 全, 施继忠, 张继业, 陈子龙
(1. 西华大学汽车测控与安全四川省重点实验室,四川 成都 610039; 2. 西华大学流体及动力机械教育部重点实验室, 四川 成都 610039; 3. 西华大学技术学院, 四川 成都 610039; 4. 浙江师范大学工学院, 浙江 金华 321004; 5. 西南交通大学牵引动力国家重点实验室, 四川 成都 610031)
Cohen-Grossberg神经网络[1]一方面在模型上包含了Hopfield神经网络、细胞神经网络、递归神经网络等,另一方面该类型神经网络在联想记忆、并行计算、非线性优化等领域具有不可取代的优势,因此对Cohen-Grossberg神经网络的动态行为的研究引起了学者们的广泛兴趣.由于在神经网络系统的硬件实现过程中,信号处理速度和传输速度有限使得时间滞后现象不可避免.时间滞后的存在不但影响神经网络系统状态的收敛性,甚至导致系统发生振荡.文献[2-5]针对几类具有时间滞后的Cohen-Grossberg神经网络平衡点的动态行为进行了研究,并取得了重要的研究成果.硬件电子网络在运行过程中容易遭受瞬间干扰,使得系统的状态发生突然变化,即出现脉冲效应.文献[6-8]建立了具有脉冲干扰的连续-离散型Cohen-Grossberg神经网络模型,研究了系统平衡点的稳定性,并分析了脉冲干扰对系统状态收敛速度的影响.文献[2-8]所得到的稳定性条件均针对定义在实数域下的Cohen-Grossberg神经网络.复数域神经网络在自适应信号处理、医学影像、通信工程、优化计算等应用领域具有实数域神经网络不可取代的优势,因此对复数域神经网络的动态行为分析成为近年的一个研究热点[9-12].文献[13]假设激活函数分别满足解析性和Lipschitz条件的情况下,对一类具有时间滞后的离散型复数域神经网络平衡点的稳定性和周期性进行了分析.SONG等[14]利用线性矩阵不等式技术及加权Lyapunov函数法,对一类具有可变时滞和脉冲干扰的复数域Hopfield神经网络的平衡点的存在性、唯一性以及模指数稳定性进行了研究.文献[15]在假设激活函数满足全局Lipschitz条件的前提下,利用矢量Lyapunov函数法和M矩阵相关原理,分析了一类具有混合时滞和脉冲干扰的复数域Hopfield神经网络平衡点的模指数稳定性.文献[16]进一步在假设复数域激活函数满足解析性的情况下,将文献[15]中的复数域神经网络模型拆分成实部系统和虚部系统,利用矢量Lyapunov函数法得到了确保该系统平衡点全局指数稳定的充分条件.文献[17]研究了具有时滞和脉冲干扰的复数域分数阶神经网络的全局渐近稳定性.文献[9-17]的研究是针对复数域Hopfield神经网络进行展开的,所取得的研究成果无法直接应用于复数域Cohen-Grossberg神经网络.ZHAO等[18]利用同胚映射和M矩阵原理对一类具有时滞的复数域Cohen-Grossberg神经网络平衡点的存在性、唯一性和模指数稳定性进行了分析.文献[18]假设Cohen-Grossberg神经网络系统中的自反馈函数是线性函数,且没有在模型中考虑脉冲干扰现象.
基于以上分析,本文将在假设复数域放大函数具有下界,并且复数域自反馈函数为非线性函数的情况下,采用同胚映射和M矩阵相关原理,对一类具有变时滞和脉冲干扰的复数域Cohen-Grossberg神经网络的平衡点的存在性、唯一性进行研究,并利用矢量Lyapunov函数法和数学归纳法,对该系统平衡点的模指数稳定性进行分析.
1 模型描述、基本假设以及引理
对于复数向量z∈Cn,令
|z|=(|z1|,|z2|,…,|zn|)T,
并定义
假设系统的神经元状态、关联矩阵、自反馈函数以及激活函数均定义在复数域的情况下,本文考虑了如下具有可变时滞和脉冲干扰的复数域Cohen-Grossberg神经网络:
(1)
式中:
i,j为神经元序号,i,j=1,2,…,n,其中n为神经元个数;
zi(t)为第i个神经元状态,zi(t)∈C,t为时间;
A和B分别为该系统的关联矩阵,A=(aij)n×n∈Cn×n,B=(bij)n×n∈Cn×n;
J(t)为系统的外部输入;
hi(zi(t))为该系统的放大函数,J(t)=(J1(t),J2(t),…,Jn(t))T∈Cn;
di(zi(t))为该系统的自反馈函数;
fi(zi(t))为该系统的激活函数;

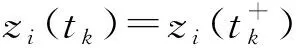
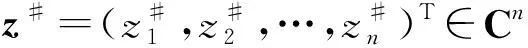
定义1若存在常数Γ>0和λ>0,对所有J∈Cn及t≥0,有
成立,则称系统(1)的平衡点z#是全局模指数稳定的.
假设1假设对所有ui(t),vi(t)∈C,存在正数ωi>0,使得复数域自反馈函数di(·)满足
注1在文献[14,16]中,令复数域激活函数可分解成实部部分和虚部部分,并要求其偏导数满足有界性和解析性.根据Liouville’s定理可知,若选取满足有界性和光滑性的复数域激活函数,则复数域激活函数只能为复数域常数,即复数域激活函数无法满足有界性和光滑性.该假设限制了人工神经网络设计时复数域激活函数的选取.此外文献[18]也指出,若复数域激活函数满足上述条件,则必满足Lipschitz条件,反之则未必成立.
为了便于设计人工神经网络时复数域激活函数的选择,对其作出如下假设.
假设2假设激活函数fi(·)满足全局Lipschitz条件,即存在Lipschitz常数li>0,使得对所有ui,vi∈C,有|fi(ui)-fi(vi)|≤li|ui-vi|成立.令L=diag(l1,l2,…,ln).
假设3假设放大函数hi(zi(t))具有下界,即假设存在正实数σi,使得hi(zi(t))满足hi(zi(t))≥σi>0.
本文所讨论的脉冲干扰作为一种外部干扰引入到系统(1)中,该扰动影响系统状态的收敛速度,即产生不利影响.因此,在对脉冲强度进行假设时只考虑脉冲强度的上界,具体如下.
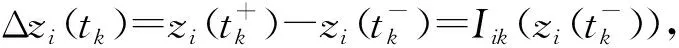
注2当系统(1)中自反馈函数是线性函数(即di(zi(t))=cizi(t),ci>0),且系统(1)中没有脉冲干扰时,则系统(1)的模型与文献[18]所研究的复数域Cohen-Grossberg神经网络是相同的.当系统(1)中放大函数hi(zi(t)=1时,且自反馈函数是线性函数时(即di(zi(t))=cizi(t),ci>0),则系统(1)的模型与文献[14]所研究的复数域Hopfield神经网络模型是相同的.以上讨论说明本文的模型更具有一般性.
引理1[7]对于矩阵P=(pij)n×n∈Rn×n,如果所有非对角元素pij≤0,i≠j,则以下的陈述是等价成立的:
(1)P为M矩阵;
(2)P的各阶顺序主子式均为正;
(3) 存在ξ∈Rn>0,使得Pξ>0;
(4)P的所有特征根的实部为正.
引理2[15]如果H(z)是定义在复数空间Cn上的连续函数,并满足如下条件:
(1)H(z)在Cn上是单叶映射,
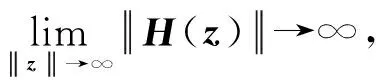
则H(z)是Cn上的同胚映射.
2 主要结论
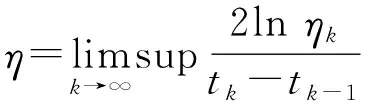
exp(0.5λτ)|bij|)<0,
(2)
那么系统(1)对于任意外部输入J∈Cn均存在唯一平衡点z#,且该平衡点是全局模指数稳定的,指数收敛率为0.5(λ-η).
证明该定理结论的证明分两个部分,分别为该系统平衡点z#的存在的性和唯一性以及在脉冲干扰下系统平衡点z#的全局模指数稳定性.
步骤Ⅰ首先利用同胚映射和M矩阵的相关原理证明该系统平衡点z#的存在的性和唯一性.
定义H(z)=(H1(z),H2(z),…,Hn(z))T是与系统(1)相关的一个映射,其中
(3)
若H(z)是Cn上的同胚映射,则显然系统(1)存在唯一平衡点z#.
(1) 首先证明H(z)是定义在Cn上的单叶映射.
由定理中不等式(2)可知不等式(4)是成立的.
(4)
根据M矩阵的相关引理1知,矩阵Q=(qij)n×n是M矩阵,其中:
此外,由于不等式(4)成立可知,存在一个充分小的正数δ>0,使得不等式(5)成立.
(5)
若存在u,v∈Cn,u=(u1,u1,…,un)T,v=(v1,v1,…,vn)T,且u≠v,使得Hi(u)=Hi(v),即
(6)
整理式(6)后,两边同时取模,有
|di(ui)-di(vi)|=
考虑到假设1和假设2,有
(7)
将式(7)进一步整理,有
lj|uj-vj|≤0,
即Q|u-v|≤0.由于Q是M矩阵,因此detQ>0且Q-1存在,故而有|u-v|=0,即u=v.也就是说Hi(z)是单叶映射,i=1,2,…,n.

即
(8)
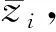
(9)
将式(9)两边同时取共轭,有
(10)
将式(9)和式(10)相加,并考虑到假设1和假设2,有
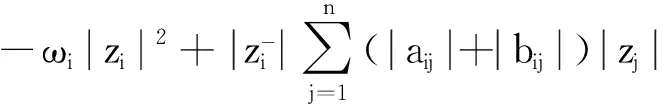
(11)
将式(11)两边同时乘ξi,并求和得到
考虑到不等式(5),可知
进一步整理上式有
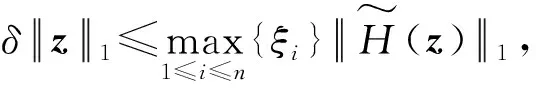
综合上述(1)和(2)的证明可知,映射H(z)是Cn上的同胚映射,因此系统(1)存在唯一平衡点z#.
步骤Ⅱ下面将利用矢量Lyapunov函数方法和数学归纳法证明系统(1)的平衡z#点在脉冲干扰下是全局模指数稳定的.

(12)
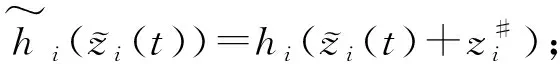
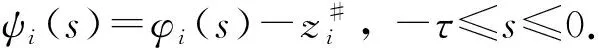
显然若证明系统(1)的平衡点z#是全局模指数稳定的,只需证明系统(12)的零解是全局模指数稳定的.
选择矢量Lyapunov函数
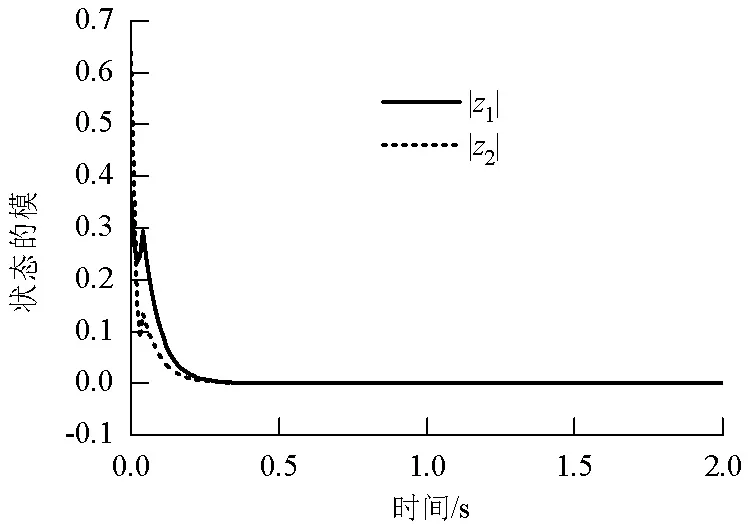
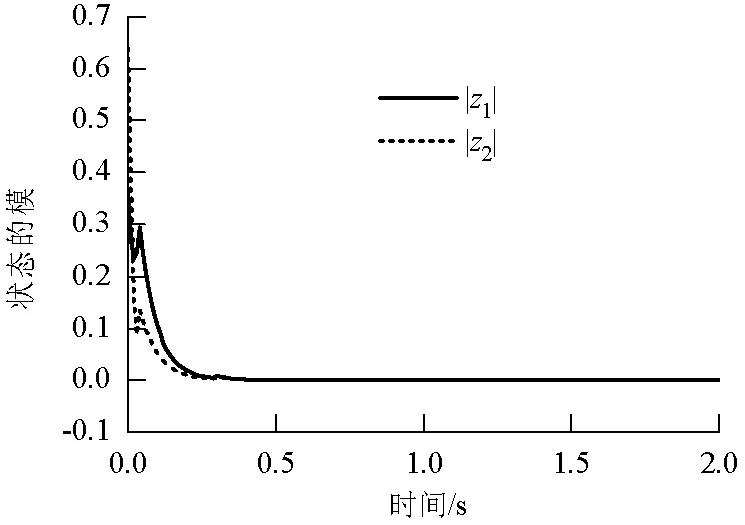
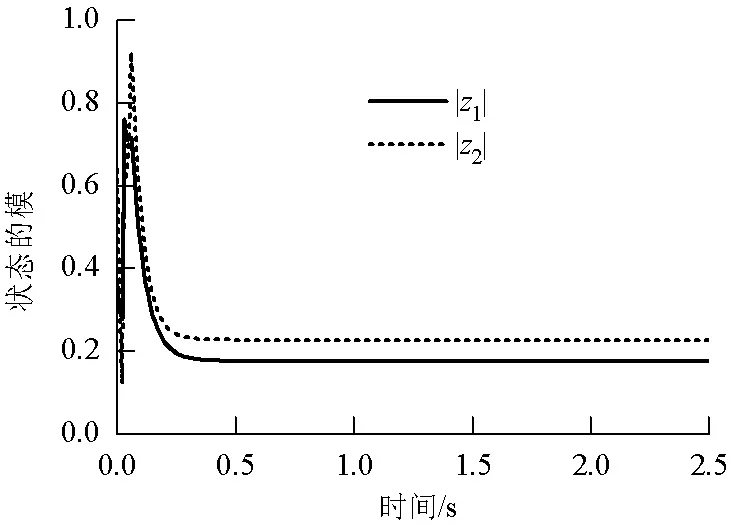
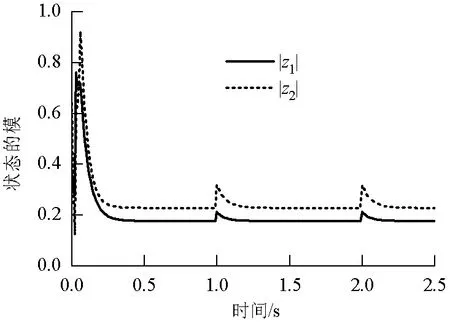
当0 (13) 令U=(U1,U2,…,Un)T, 即 D+0Vi(t)=2Ui(t)D+Ui(t). 将其代入到不等式(13)中,有 (14) 进一步可得Ui(t)<ξiχ0,0 tk-1≤t (15) t0≤t 其中η0=1.根据前面的分析可知该式显然是成立的. 假设不等式(16)成立, tw-1≤t (16) 由于ηw≥1,进而不等式(16)变为 tw-τ≤t≤tw. (17) ηw-1ηwξiχ0,tw≤t≤tw+1. (18) ηw-1ηwξm*χ0,tw≤t* ηw-1ηwξjχ0,tw-τ (20) 将式(19)和式(20)代入到不等式(14)中,并考虑到不等式(2),有 D+0Um*(t*)≤ η0η1η2…ηw-1ηwχ0<0. 这与假设D+0Um*(t*)≥0是矛盾的,因此不等式(16)是成立的. tk-1≤t (21) ηk≤exp(0.5η(tk-tk-1)), exp(0.5η(t2-t1))… exp(0.5η(tk-1-tk-2))ξiχ0exp(-0.5λt)< tk-1≤t 进一步,有 exp(-0.5(λ-η)(t-t0))= 根据定义1可知,系统(12)的零解是全局模指数稳定的,即系统(1)的平衡点z#是全局模指数稳定的,即 综合步骤Ⅰ和步骤Ⅱ可知,系统(1)存在唯一平衡点z#,且该平衡点是在脉冲干扰下是全局模指数稳定的,指数收敛率为0.5(λ-η).证毕. 注3容易验证当系统(1)中的神经元状态、关联矩阵以及各函数定义在实数域时,本文的研究方法和所建立的判据对相应的实值神经网络仍适用. 注4若系统(1)中没有脉冲干扰,此时确保系统(1)平衡点存在性、唯一性和全局模指数稳定性的充分条件则为:若假设1~3是成立的,并且矩阵Q是M矩阵,其中: 则系统(1)存在唯一平衡点,且该平衡点是全局模指数稳定的. 注5当神经网络实际应用于联想记忆时,系统具有多个平衡点,此时需分析确保该系统多平衡点的Lagrange稳定性或多稳定性,见文献[19-20].当神经网络实际应用于优化计算时,期望系统具有唯一的平衡点,此时需分析确保系统平衡点的存在性和唯一性.本文基于矢量Lyapunov函数法和M矩阵理论得到了确保系统平衡点存在性、唯一性和Lyapunov意义下的全局模指数稳定的充分条件.此外,本文放宽了文献[18]对放大函数和自反馈函数的限制,并考虑了脉冲干扰对系统的影响,所得到的结论更具有一般性. 考虑如式(22)复数域Cohen-Grossberg神经网络系统, (22) 情况1假设已知: 加权矩阵分别为 激活函数为 脉冲发生时刻为 {0.3 s,0.9 s,1.2 s…}; λ=8; ξ=(0.5,0.7)T. 经计算,有ω1=8,ω2=5,σ1=2,σ2=3,l1=0.250,l2=0.375,η=6.86. 令系统(22)中的时延为 τ1j=0.02-0.01sint, τ2j=0.03-0.01cost, j=1,2,t≥0. 显然τ=0.04 s. 令初始条件为 z1(s)=0.3-0.2i,z2(s)=-0.5+0.4i, s∈[-0.04,0], J1(t)=0,J2(t)=0. 进一步计算有 exp(0.5λτ)|b1j|)=-0.860<0, exp(0.5λτ)|b2j|)=-0.591<0. 容易验证以上条件满足定理的假设,故根据定理可得结论:系统(22)存在唯一零解,且该零解是全局模指数稳定的,指数收敛率为0.57.关于系统(22)的仿真结果见图1和图2,图1给出了没有脉冲干扰时系统(22)的神经元状态z1(t)和z2(t)的模曲线,图2给出了在脉冲干扰影响下系统(22)的神经元状态z1(t)和z2(t)的模曲线.由仿真结果可知该系统状态的模是收敛的.仿真结果验证了本文结论的正确性. 图1 情况1下无脉冲干扰时系统(22)状态的模曲线Fig.1 Module curves of neuro states of Eq.(22) without impulsive disturbances under case 1 图2 情况1脉冲干扰下系统(22)状态的模曲线Fig.2 Module curves of neuro states of Eq.(22) with impulsive disturbances under case 1 图3 情况2下无脉冲干扰时系统(22)状态的模曲线Fig.3 Module curves of neuro states of Eq.(22) without impulsive disturbances under case 2 图4 情况2下脉冲干扰下系统(22)状态的模曲线Fig.4 Module curves of neuro states of Eq.(22) with impulsive disturbances under case 2 针对一类具有脉冲干扰和可变时滞的复数域Cohen-Grossberg神经网络,在假设复数域放大函数具有下界且复数域自反馈函数为非线性函数的情况下,采用同胚映射和M矩阵相关原理对该系统平衡点的存在性、唯一性进行了研究,然后利用矢量Lyapunov函数法和数学归纳法得到了确保该系统平衡点的全局模指数稳定性的充分条件.本文所得到的判据同时显示了时滞和脉冲干扰对系统平衡点动态行为的影响,即时滞越大,脉冲干扰强度越大,系统神经元状态的收敛速度则越慢.该研究成果不但推广了现有结论,并且具有较低的保守性.最后给出的两个数值算例验证了本文结论的可行性,同时算例仿真结果证明了结论的正确性. 致谢:流体及动力机械教育部重点实验室研究基金 (szjj2016-007); 汽车测控与安全四川省重点实验室研究基金(szjj2017-074).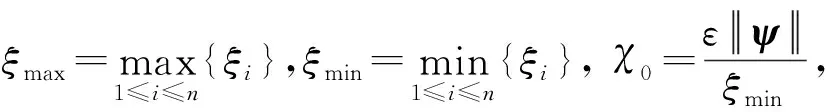
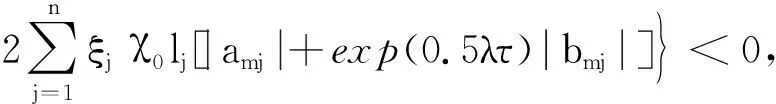
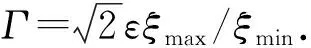
3 数值仿真算例

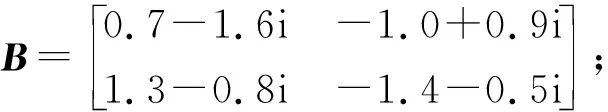

4 结 论
